一.组合数:
问题引入:现在有 n 个球,取其中的 k 个球,问一共有多少
种方式?
答案:
公式直观解释:
我们考虑有顺序地取出 k 个球:第一次有 n 种选择,第二次有 n-1 种
选择,...,第 k 次有 n-k+1 种选择。故一共有

种方案数;但如果不计算顺序的话,那么对于一种方案,其实有 k! 种
不同的顺序,所以再除以 k! 即为最终的答案。
实际编程所需要的公式:C(n,k) = C(n − 1,k) + C(n − 1,k − 1)
题目:
luogu 2822 组合数问题(边计算边模)
luogu 1313 计算系数(答案为:a n × b m × C(k,n))
二.计数问题:
(1). 把 n 个数拆成 k 个非负整数,有多少种方案数?C(n,k)
(2). 把 n 个数拆成 k 个正整数,有多少种方案数?C(n,n-k+1)
1.放球问题:
1. 把 N 个不同的球放在 K 个不同箱子-----n^k
2. N 个相同的球放在 k 个不同的箱子-----C(n,n-k)
3. N 个不同的球放在 k 个相同的箱子
4. N 个相同的球放在 k 个相同的箱子
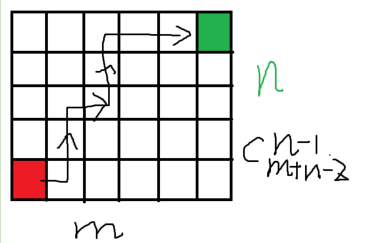
2.路径行走:
一个 N*M 的网格,每次只能向上或者向右,从左下角到右上角有
多少种方案数
C(n + m − 2,n − 1)
按照字典序的顺序从小写字母 a 开始按顺序给出序列 (序列中都为升序字符串,挑出长度位 L 的字符串有多少个?
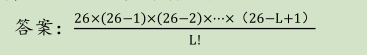
练习:
(1)Codevs 1262 不要把球传我
(2)HDU 5698 瞬间移动
(3)HDU 1465
{
错排公式:设 F[i] 为每个数都不在自己的位置上的排列数。
* 则有公式 F[i] = (n-1) (F[i-1] + F[i-2])
假设在第 1 个位置上的是 k(k ̸= 1),则有两种情况:
1 在 k 的位置上的是 1。则这时候只需要要求其他的 n-2 个数不在
位置上即可。
2 在 k 的位置上不是 1。把 1 看作 k,相当于 n-1 个数都不在自己的
位置上。
}
(4)HDU 4704 Sum
{

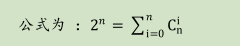
}