Q1(poj 3070):
求斐波那契数列的第n个,n最大取到1000000000,。
分析:求这种较大递推数列的一般方法使用矩阵快速幂的,这里题目直接给出了矩阵形式,就不需要进行友矩阵(A)的构造了,也不需要进行最后一次矩阵和向量的相乘,直接初始化矩阵规模,进行快速幂即可。
不过这个结论倒是可以记住,以后就有了logn求斐波那契数列的方法:
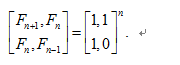
参考代码如下:
#include<iostream> #include<string> #include<cstring> using namespace std; const int maxn = 20; typedef long long Matrix[maxn][maxn]; typedef long long Vector[maxn]; int sz , mod; void matrix_mul(Matrix A , Matrix B , Matrix res)//矩阵A*B = C , O(n^3).矩阵均为同阶方阵 { Matrix C; memset(C , 0 , sizeof(C)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz; j++) for(int k = 0;k < sz; k++) C[i][j] = (C[i][j] + A[i][k] * B[k][j])%mod; memcpy(res , C , sizeof(C)); } void matrix_pow(Matrix A , int n , Matrix res)//矩阵快速幂O(logn) { Matrix a , r; memcpy(a , A , sizeof(a)); memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) r[i][i] = 1;//单位矩阵 while(n){ if(n&1) matrix_mul(r , a , r); n >>= 1; matrix_mul(a , a , a); } memcpy(res , r , sizeof(r)); } void Transform(Vector d , Matrix A , Vector res)//计算完A^(n-d)之后,这个函数计算A*d = res { Vector r; memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz;j++) r[i] = (r[i] + d[j] * A[i][j])%mod; memcpy(res , r , sizeof(r)); } int main() { int n; while(cin >>n) { if(n == -1) break; if(n == 0) {cout<<0<<endl;continue;} mod = 10000; sz = 2; Vector a , f; Matrix A; memset(A , 0 , sizeof(A)); A[0][0] = 1; A[0][1] = 1; A[1][0] = 1; A[1][1] = 0; matrix_pow(A , n - 1 , A); cout << A[0][0] << endl; } return 0; }
Q2(hdu 5950):
一个数列的递推关系式是f[i] = f[i-1] + 2f[i-2] + i^4,现在给出n(最大可取1000000000),计算f[n]%mod的结果。
分析:这道题的核心方法就是上面我们提到的时间复杂度为O(logn)求递推关系的矩阵快速幂。而这个方法的关键就是快速幂的底数A,需要一定的推导技巧。


#include<iostream> #include<string> #include<cstring> using namespace std; const int maxn = 20; typedef long long Matrix[maxn][maxn]; typedef long long Vector[maxn]; int sz ; long long mod = 2147493647; void matrix_mul(Matrix A , Matrix B , Matrix res)//矩阵A*B = C , O(n^3).矩阵均为同阶方阵 { Matrix C; memset(C , 0 , sizeof(C)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz; j++) for(int k = 0;k < sz; k++) C[i][j] = (C[i][j] + A[i][k] * B[k][j])%mod; memcpy(res , C , sizeof(C)); } void matrix_pow(Matrix A , int n , Matrix res)//矩阵快速幂O(logn) { Matrix a , r; memcpy(a , A , sizeof(a)); memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) r[i][i] = 1;//单位矩阵 while(n){ if(n&1) matrix_mul(r , a , r); n >>= 1; matrix_mul(a , a , a); } memcpy(res , r , sizeof(r)); } void Transform(Vector d , Matrix A , Vector res)//计算完A^(n-d)之后,这个函数计算A*d = res { Vector r; memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz;j++) r[i] = (r[i] + d[j] * A[i][j])%mod; memcpy(res , r , sizeof(r)); } int main() { long long n , a , b; int t; cin>>t; while(t--) { cin>>n>>a>>b; sz = 7; //矩阵A的规模是sz Vector f; if(n == 1) {cout<<a<<endl;continue;} if(n == 2) {cout<<b<<endl;continue;} f[0] = b;f[1] = a; f[2] = 16;f[3] = 8;f[4] = 4;f[5] = 2;f[6] = 1; Matrix A; memset(A , 0 , sizeof(A));//注意每次矩阵A的参数都要初始化. A[0][0] = 1;A[0][1] = 2;A[0][2] = 1;A[0][3] = 4;A[0][4] = 6;A[0][5] = 4;A[0][6] = 1; A[1][0] = 1; A[2][2] = 1;A[2][3] = 4;A[2][4] = 6;A[2][5] = 4;A[2][6] = 1; A[3][3] = 1;A[3][4] = 3;A[3][5] = 3;A[3][6] = 1; A[4][4] = 1;A[4][5] = 2;A[4][6] = 1; A[5][5] = 1;A[5][6] = 1; A[6][6] = 1; matrix_pow(A , n - 2 , A); Transform(f , A , f); cout << f[0] << endl; } return 0; }
Q3(uva 10689):
这道题目是矩阵快速幂求斐波那契数列的推广形式,给出f[0],f[1]的初值,递推关系式斐波那契数列的递推关系f[n]=f[n-1]+f[n-2].
分析:由于递推关系和斐波那契数列的递推关系一致,友矩阵Q是一样的.
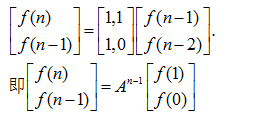


#include<iostream> #include<string> #include<cstring> #include<cmath> using namespace std; const int maxn = 20; typedef long long Matrix[maxn][maxn]; typedef long long Vector[maxn]; int sz , mod; void matrix_mul(Matrix A , Matrix B , Matrix res)//矩阵A*B = C , O(n^3).矩阵均为同阶方阵 { Matrix C; memset(C , 0 , sizeof(C)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz; j++) for(int k = 0;k < sz; k++) C[i][j] = (C[i][j] + A[i][k] * B[k][j])%mod; memcpy(res , C , sizeof(C)); } void matrix_pow(Matrix A , int n , Matrix res)//矩阵快速幂O(logn) { Matrix a , r; memcpy(a , A , sizeof(a)); memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) r[i][i] = 1;//单位矩阵 while(n){ if(n&1) matrix_mul(r , a , r); n >>= 1; matrix_mul(a , a , a); } memcpy(res , r , sizeof(r)); } void Transform(Vector d , Matrix A , Vector res)//计算完A^(n-d)之后,这个函数计算A*d = res { Vector r; memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz;j++) r[i] = (r[i] + d[j] * A[i][j])%mod; memcpy(res , r , sizeof(r)); } int main() { int a , b , m , n; int t; cin>>t; while(t--) { cin >> a >> b >> n >>m; mod = 10; sz = 2; for(int i = 1;i < m;i++) mod *= 10; Vector f; Matrix A; f[1] = a; f[0] = b; //列向量[f(d) , f(d-1) , f(d-2) , ... , f(1)] memset(A , 0 , sizeof(A));//得到配出来的常数矩阵A A[0][0] = 1;A[0][1] = 1; A[1][0] = 1;A[1][1] = 0; matrix_pow(A , n - 1 , A); Transform(f , A , f); cout << f[0] << endl; } return 0; }
Q4(hdu4565):


Q5(hdu2256):



#include<iostream> #include<string> #include<cstring> #include<cstdio> using namespace std; const int maxn = 20; typedef long long Matrix[maxn][maxn]; typedef long long Vector[maxn]; int sz , mod; void matrix_mul(Matrix A , Matrix B , Matrix res)//矩阵A*B = C , O(n^3).矩阵均为同阶方阵 { Matrix C; memset(C , 0 , sizeof(C)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz; j++) for(int k = 0;k < sz; k++) C[i][j] = (C[i][j] + A[i][k] * B[k][j])%mod; memcpy(res , C , sizeof(C)); } void matrix_pow(Matrix A , int n , Matrix res)//矩阵快速幂O(logn) { Matrix a , r; memcpy(a , A , sizeof(a)); memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) r[i][i] = 1;//单位矩阵 while(n){ if(n&1) matrix_mul(r , a , r); n >>= 1; matrix_mul(a , a , a); } memcpy(res , r , sizeof(r)); } void Transform(Vector d , Matrix A , Vector res)//计算完A^(n-d)之后,这个函数计算A*d = res { Vector r; memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz;j++) r[i] = (r[i] + d[j] * A[i][j])%mod; memcpy(res , r , sizeof(r)); } int main(){ int n , T; scanf("%d" , &T); while(T--){ scanf("%d" , &n); mod = 1024;//整个数值在m的剩余系下 sz = 2;//矩阵A的规模是sz if(n == 0) {printf("1 ");continue;} Vector a , f; Matrix A; //A是矩阵,a是递推公式的系数向量 f是数列的初值向量 f[0] = 1; f[1] = 0; //列向量[f(d) , f(d-1) , f(d-2) , ... , f(1)] //数学概念上向量从1开始,但是存储上f[]数组是从0开始的,这点一定要注意!!逻辑高位存储在存储结构的地位,这里非常容易错! memset(A , 0 , sizeof(A));//得到配出来的常数矩阵A A[0][0] = 5;A[0][1] = 12; A[1][0] = 2;A[1][1] = 5; matrix_pow(A , n , A); Transform(f , A , f); printf("%d " ,(2 * f[0] - 1) %mod); } return 0; }
Q6(hdu5451):


#include<iostream> #include<string> #include<cstring> #include<cstdio> using namespace std; const int maxn = 20; typedef long long Matrix[maxn][maxn]; typedef long long Vector[maxn]; typedef long long LL; int sz , mod; void matrix_mul(Matrix A , Matrix B , Matrix res)//矩阵A*B = C , O(n^3).矩阵均为同阶方阵 { Matrix C; memset(C , 0 , sizeof(C)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz; j++) for(int k = 0;k < sz; k++) C[i][j] = (C[i][j] + A[i][k] * B[k][j])%mod; memcpy(res , C , sizeof(C)); } void matrix_pow(Matrix A , int n , Matrix res)//矩阵快速幂O(logn) { Matrix a , r; memcpy(a , A , sizeof(a)); memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) r[i][i] = 1;//单位矩阵 while(n){ if(n&1) matrix_mul(r , a , r); n >>= 1; matrix_mul(a , a , a); } memcpy(res , r , sizeof(r)); } void Transform(Vector d , Matrix A , Vector res)//计算完A^(n-d)之后,这个函数计算A*d = res { Vector r; memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz;j++) r[i] = (r[i] + d[j] * A[i][j])%mod; memcpy(res , r , sizeof(r)); } LL Quick_Mod(LL a, LL b, int m){ LL res = 1,term = a % m; while(b) { if(b & 1) res = (res * term) % m; term = (term * term) % m; b >>= 1; } return res%m; } int main(){ int T; LL x; scanf("%d" , &T); for(int kase = 1;kase <= T;kase++){ scanf("%lld %d" , &x , &mod); sz = 2;//矩阵A的规模是sz Vector a , f; Matrix A; //A是矩阵,a是递推公式的系数向量 f是数列的初值向量 f[0] = 1; f[1] = 0; x = Quick_Mod(2 , x , mod * mod - 1) + 1; if(x == 0) {printf("1 ");continue;} //列向量[f(d) , f(d-1) , f(d-2) , ... , f(1)] //数学概念上向量从1开始,但是存储上f[]数组是从0开始的,这点一定要注意!!逻辑高位存储在存储结构的地位,这里非常容易错! memset(A , 0 , sizeof(A));//得到配出来的常数矩阵A A[0][0] = 5;A[0][1] = 12; A[1][0] = 2;A[1][1] = 5; matrix_pow(A , x , A); Transform(f , A , f); printf("Case #%d: %d " ,kase , (2 * f[0] - 1) %mod); } return 0; }
Q7(hdu6198):
基于斐波那契数列,给出整数k,让你计算k个允许重复的斐波那契数列,不能组成的最小整数是多少。
分析:通过手动算找规律,编程打表找规律也好,找到规律问题的本质是让我们求fib(2n + 3)-1.然后简单一发矩阵快速幂即可。
Q8(hdu6185):
用1x2的格子覆盖4xn的格子,问有多少种不同的方案,结果对1e9+7取模。
分析:这道题目算是很综合了。纯粹基于覆盖的机理找递推关系难度较大,可以通过dfs找到小数据的表,我们根据n的取值,也能够猜测这道题目应该是有线性递推的关系的。这里在拿到了前十项的数据之后,找规律有个小套路,最基本的是靠观察,但是对于含有2项以上的线性递推关系,这个方法就不是很好了。这里我们依次假设题目有如下的线性递推关系:
(1)f(n) = a*f(n-1)+b*f(n-2)
(2)f(n) = a*f(n-1)+b*f(n-2)+c*f(n-3)
(3)f(n)=a*f(n-1)+b*f(n-2)+c*f(n-3)+d*f(n-4)
...
然后基于原始数据,构造线性方程组再用高斯消元求解a、b等参数进行验证,当得到系数均为整数的时候,即题目满足的线性递推关系。
找到了线性递推关系之后,用矩阵快速幂跑一发即可。
Q9(hdu4965):



#include<iostream> #include<string> #include<cstring> #include<cstdio> using namespace std; const int maxn = 1000 + 1; typedef long long Matrix1[maxn][6]; typedef long long Matrix2[6][maxn]; typedef long long Matrix3[6][6]; int sz , mod; void matrix_mul(Matrix3 A , Matrix3 B , Matrix3 res)//矩阵A*B = C , O(n^3).矩阵均为同阶方阵 { Matrix3 C; memset(C , 0 , sizeof(C)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz; j++) for(int k = 0;k < sz; k++) C[i][j] = (C[i][j] + A[i][k] * B[k][j])%mod; memcpy(res , C , sizeof(C)); } void matrix_mul_p1(Matrix2 B , Matrix1 A, int sz1 , int sz2, int sz3 , Matrix3 res){//sz1*sz2的矩阵与sz2*sz3的矩阵做乘法 Matrix3 C; memset(C , 0 , sizeof(C)); for(int i = 0;i < sz1;i++) for(int j = 0;j < sz3;j++) for(int k = 0;k < sz2;k++) C[i][j] = (C[i][j] + B[i][k]*A[k][j]); memcpy(res , C , sizeof(C)); } void matrix_mul_p2(Matrix1 A , Matrix3 C, int sz1 , int sz2, int sz3 , Matrix1 res){//sz1*sz2的矩阵与sz2*sz3的矩阵做乘法 Matrix1 temp; memset(temp , 0 , sizeof(temp)); for(int i = 0;i < sz1;i++) for(int j = 0;j < sz3;j++) for(int k = 0;k < sz2;k++) temp[i][j] = (temp[i][j] + A[i][k]*C[k][j])%mod; memcpy(res , temp , sizeof(temp)); } int matrix_mul_p3(Matrix1 A , Matrix2 B, int sz1 , int sz2, int sz3){//sz1*sz2的矩阵与sz2*sz3的矩阵做乘法 int temp ,ans; temp = 0;ans = 0; for(int i = 0;i < sz1;i++){ for(int j = 0;j < sz3;j++){ temp = 0; for(int k = 0;k < sz2;k++) temp = (temp + A[i][k]*B[k][j])%mod; ans += temp; } } return ans; } void matrix_pow(Matrix3 A , int n , Matrix3 res)//矩阵快速幂O(logn) { Matrix3 a , r; memcpy(a , A , sizeof(a)); memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) r[i][i] = 1;//单位矩阵 while(n){ if(n&1) matrix_mul(r , a , r); n >>= 1; matrix_mul(a , a , a); } memcpy(res , r , sizeof(r)); } int main(){ int n , k; while(scanf("%d%d" , &n , &k)){ Matrix1 A; Matrix2 B; Matrix3 C; mod = 6; for(int i = 0;i < n;i++) for(int j = 0;j < k;j++) scanf("%lld" , &A[i][j]); for(int i = 0;i < k;i++) for(int j = 0;j < n;j++) scanf("%lld" , &B[i][j]); matrix_mul_p1(B , A , k , n , k , C); sz = k; matrix_pow(C , n*n - 1, C); //下面要做n*k的A * k*k的C * k*n的B matrix_mul_p2(A , C , n , k , k , A); int ans = matrix_mul_p3(A , B , n , k , n); printf("%d " , ans); } return 0; } //lrj的快速幂模板迷之超时,下面贴一个ac代码 /* #include <cstdio> #include <cstring> #include <cmath> #include <cstdlib> #include <iostream> #include <algorithm> #include <queue> #include <map> #include <set> #include <vector> #include <cctype> using namespace std; const int mod=6; struct matrix{ int f[6][6]; }; int A[1001][6],B[6][1001],C[1001][6],D[1001][1001]; matrix mul(matrix a,matrix b,int n) { matrix c; memset(c.f,0,sizeof(c.f)); int i,j,k; for(i=0;i<n;i++) { for(j=0;j<n;j++) { for(k=0;k<n;k++) { c.f[i][j]+=a.f[i][k]*b.f[k][j]; } c.f[i][j]%=mod; } } return c; } matrix pow_mod(matrix a,int b,int n) { matrix s; memset(s.f,0,sizeof(s.f)); for(int i=0;i<n;i++)s.f[i][i]=1; while(b) { if(b&1)s=mul(s,a,n); a=mul(a,a,n); b=b>>1; } return s; } int main() { int n,K; while(scanf("%d%d",&n,&K)!=EOF) { if(n==0&&K==0)break; int i,j,k; for(i=0;i<n;i++) for(j=0;j<K;j++) scanf("%d",&A[i][j]); for(i=0;i<K;i++) for(j=0;j<n;j++) scanf("%d",&B[i][j]); matrix e,g; memset(e.f,0,sizeof(e.f)); for(i=0;i<K;i++) { for(j=0;j<K;j++) { for(k=0;k<n;k++) e.f[i][j]+=B[i][k]*A[k][j]; e.f[i][j]%mod; } } e=pow_mod(e,n*n-1,K); for(int i = 0;i < K;i++){ for(int j =0;j < K;j++) printf("%d " , e.f[i][j]); printf(" "); } memset(C,0,sizeof(C)); for(i=0;i<n;i++) { for(j=0;j<K;j++) { for(k=0;k<K;k++) C[i][j]+=A[i][k]*e.f[k][j]; C[i][j]%=mod; } } for(int i = 0;i < n;i++){ for(int j =0;j < K;j++) printf("%d " , C[i][j]); printf(" "); } int ans=0; memset(D,0,sizeof(D)); for(i=0;i<n;i++) { for(j=0;j<n;j++) { for(k=0;k<K;k++) D[i][j]+=C[i][k]*B[k][j]; ans+=D[i][j]%mod; } } printf("%d ",ans); } return 0; } */
Q10(hdu4990):
利用题目给出的代码所呈现的机制,输入n、m输出对应的答案。
分析:这是一个典型的优化代码题目。能够看到m是mod运算使用的,可以不考虑。然后对于不同的n,我们通过题目给出的程序可以得到n取[0,11]的答案。
a[n]:0 1 2 5 10 21 42 85 170 341 682 1365.
题目其实就是快速求解这个数列.根据观察得,这个数列满足f[n] = f[n-1]+2f[n-2]+1的递推关系。然后矩阵快速幂构造一发即可。

#include<cstdio> #include<string> #include<cstring> using namespace std; const int maxn = 20; typedef long long Matrix[maxn][maxn]; typedef long long Vector[maxn]; int sz , mod; void matrix_mul(Matrix A , Matrix B , Matrix res)//矩阵A*B = C , O(n^3).矩阵均为同阶方阵 { Matrix C; memset(C , 0 , sizeof(C)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz; j++) for(int k = 0;k < sz; k++) C[i][j] = (C[i][j] + A[i][k] * B[k][j])%mod; memcpy(res , C , sizeof(C)); } void matrix_pow(Matrix A , int n , Matrix res)//矩阵快速幂O(logn) { Matrix a , r; memcpy(a , A , sizeof(a)); memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) r[i][i] = 1;//单位矩阵 while(n){ if(n&1) matrix_mul(r , a , r); n >>= 1; matrix_mul(a , a , a); } memcpy(res , r , sizeof(r)); } void Transform(Vector d , Matrix A , Vector res)//计算完A^(n-d)之后,这个函数计算A*d = res { Vector r; memset(r , 0 , sizeof(r)); for(int i = 0;i < sz;i++) for(int j = 0;j < sz;j++) r[i] = (r[i] + d[j] * A[i][j])%mod; memcpy(res , r , sizeof(r)); } int main(){ int n , m; while(~scanf("%d%d" , &n ,&m)){ mod = m;sz = 4; Vector a , f; Matrix A; f[0] = 2; f[1] = 1; f[2] = 0; f[3] = 1; memset(A , 0 , sizeof(A)); A[0][0] = 1;A[0][1] = 2;A[0][2] = 0;A[0][3] = 1; A[1][0] = 1;A[1][1] = 0;A[1][2] = 0;A[1][3] = 0; A[2][0] = 0;A[2][1] = 1;A[2][2] = 0;A[2][3] = 0; A[3][0] = 0;A[3][1] = 0;A[3][2] = 0;A[3][3] = 1; if(n ==0) {printf("0 "); continue;} else if(n == 1) {printf("%d " , 1 % mod); continue;} else if(n == 2) {printf("%d " , 2 % mod); continue;} matrix_pow(A , n - 2 , A); Transform(f , A , f); printf("%d " , f[0]); } return 0; }
当然还有比较傻瓜的做法是,根据手头的数据,推测线性递推关系然后构造线性方程组再用高斯消元(上文一个题目用到过)。这里值得注意的是,推测线性递推关系中,应该考虑常数项的,这样相对上面(Q8:hdu6185),实际就是多了一个自变量。
高斯消元的代码如下:

#include <iostream> #include <cstdio> #include <cmath> #include <cstring> #include <algorithm> #include <cstring> #include <vector> using namespace std; const int maxn=105; typedef double Matrix[maxn][maxn]; Matrix A,S; //n是方程的个数 void gauss(Matrix A,int n){ int i,j,k,r; for(int i=0; i<n; i++) { r=i; for( j=i+1; j<n; j++) if(fabs(A[j][i])>fabs(A[r][i]))r=j; if(r!=i) for(j=0; j<=n; j++)swap(A[r][j],A[i][j]); for(k=i+1; k<n; k++) { double f=A[k][i]/A[i][i]; for(j=i; j<=n; j++) A[k][j]-=f*A[i][j]; } } for(i=n-1; i>=0; i--) { for(j=i+1; j<n; j++) A[i][n]-=A[j][n]*A[i][j]; A[i][n]/=A[i][i]; } } int main() { memset(A,0,sizeof(A)); A[0][0]=1,A[0][1]=0,A[0][2]=1; A[1][0]=2,A[1][1]=1,A[1][2]=1; A[2][0]=5,A[2][1]=2,A[2][2]=1; //对于线性方程组Ax = b 代码中的A是[A,b] A[0][3]=2,A[1][3]=5,A[2][3]=10; gauss(A,3); //经过该代码实现的高斯消元,解向量x是A矩阵的最后一列,即替代了原来的系数向量 for(int i=0; i<3; i++) printf("%8.2f ",A[i][3]); return 0; }
可求方程组的解集是[1,2,1],对应着我们构造线性方程组的方式,可得到递推关系:f[n] = f[n-1] + 2f[n-2]+1.
