在许多生产时间问题中,我们根据已知条件往往会列出一个一元非线性方程,一个最典型的例子就是银行存款的问题,由于其利息需要基于前一年的本息和,因此列出来的方程x的指数往往是高次的。还有物理问题当中一系列用微分方程导出的一元非线性方程。因此如何求解一元非线性方程,是计算数学要解决的重要问题之一。
牛顿法:
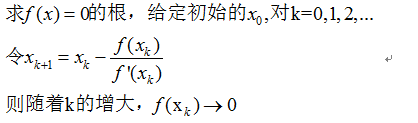
牛顿法可以通过Taylor定理导出:

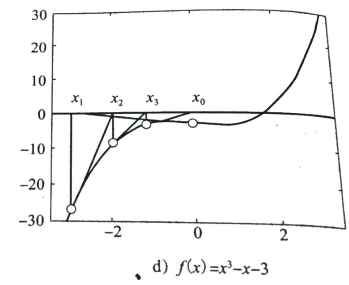
不幸的是,单纯的牛顿法并不是使用所有情况的,下面给出一个经过较为精确的绘图利用牛顿迭代最终无解的情况: