《程序设计中的组合数学》——指数型母函数

   承接上文对于普通型母函数的理论，这次讨论的是指数型母函数。对比二者来看，普通型母函数适用于解决组合型的问题，而指数型母函数则是解决排列型问题。

    在构造普通型的母函数的时候，我们赋予f(x)=(1 + x)^n各个字母（包括1）丰富的物理含义，同样，在构造指数型母函数   f(x) = (1 + x^m/m!)^n，各个字母同样具有丰富的物理含义。

    通过上一篇文章的探索，我们已经了解，普通型母函数的展开式中各项的系数其实就是对应该组合下(x的指数表示的物理含义)的组合数，而现在我们想得到的是排列数，同时由排列和组合的关系（组合数乘以阶乘是排列数 ），我们可以在母函数的展开式中的系数中提取出一个阶乘数，这样，此时该项数的系数即是原来的排列数乘以对应的阶乘，即可得到排列数。而此时每一项构造出的x^j / j!实际上就是指数型母函数的标志函数。

  给出定理如下。

    

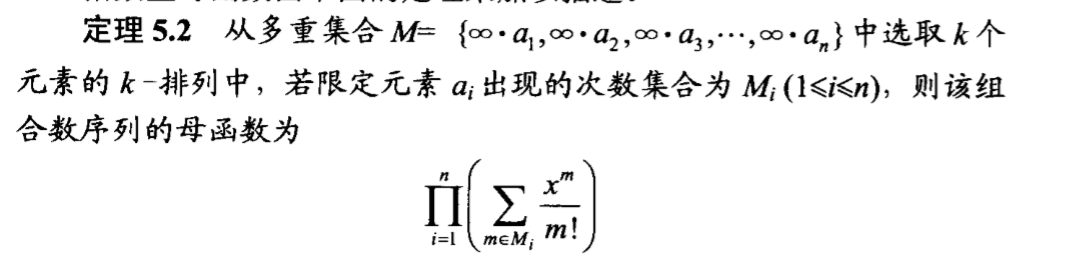
   值得一提的是，从普通型母函数到指数型母函数的过渡，是有一定的条件的，在构造普通型母函数时，我们可以给予每个单项式 (1 + x^m)的指数m丰富的物理含义（砝码的质量等），但是在构造指数型母函数的是时候，往往m只能是某个元素出现的次数(应为这样才有进行排列的意义)，而既然m表示某个元素出现次数了，在最后得出组合数提出阶乘得到排列数的时候，遇到相同元素进行阶乘全排列的时候会出现重复的情况，因此，在每个单项式x^m的系数前面应当除以该元素出现次数的全排列，即——m！   这便是指数型母函数的由来。
  不妨看看一个典型指数型母函数的问题。(Problem source : 2065)

Problem Description

医学界发现的新病毒因其蔓延速度和Internet上传播的"红色病毒"不相上下,被称为"红色病毒",经研究发现,该病毒及其变种的DNA的一条单链中,胞嘧啶,腺嘧啶均是成对出现的。    现在有一长度为N的字符串,满足一下条件: (1) 字符串仅由A,B,C,D四个字母组成; (2) A出现偶数次(也可以不出现); (3) C出现偶数次(也可以不出现); 计算满足条件的字符串个数. 当N=2时,所有满足条件的字符串有如下6个:BB,BD,DB,DD,AA,CC. 由于这个数据肯能非常庞大,你只要给出最后两位数字即可.

  理解了上述指数型母函数的构造过程，这题在数学建模上十分容易。  

  随后结合高等数学e^x泰勒展开式进行化简运算，同时寻求结果的周期性变化规律。  

   代码如下。 有点小bug不是ac代码，时间紧迫先贴出来了。

#include<stdio.h>
#include<math.h>


int main()
{

 

    __int64 a[25] , b[25];
    int i;
    for(i = 3;i <= 22;i++)
     {
        a[i] = ((pow(4 , i) + 2*pow(2 , i )) / 4 ) ;
        b[i - 2] = a[i];
     }

  int T;
  __int64 n;


      //printf("%I64d
",a[21]);

  while(scanf("%d",&T) != EOF && T)
  {
    for(i = 1;i <= T;i++)
    {

     scanf("%I64d",&n);
     getchar();
     printf("Case %d: ",i);
        if(n == 0)
              printf("1
");
        else if(n == 1 )
              printf("2
");
        else if(n == 2)
              printf("6
");
        else
        {
             if((n - 2)%20 == 0)
                  printf("Case %d: %d
",i,b[20] % 100);
             else
                  printf("Case %d: %d
",i,b[(n-2) % 20 ] % 100 );
        }

 

 

    }
     printf("
");
  }
}

  可以看到这一题面对庞大的数据量，通过理论的应用和数学的推导，极大降低了算法的时间复杂度，想必这就是理论之美、数学之美的一撇体现。
  让我们再来一道简单的指数型母函数的题目(Problem source : hdu 1521)。

Problem Description

有n种物品，并且知道每种物品的数量。要求从中选出m件物品的排列数。例如有两种物品A,B，并且数量都是1，从中选2件物品，则排列有"AB","BA"两种。

 

Input

每组输入数据有两行，第一行是二个数n,m(1<=m,n<=10)，表示物品数，第二行有n个数，分别表示这n件物品的数量。

  很典型的指数型母函数的题目，都不需要对题目进行抽象就可以知道，因为题目给出的描述就很抽象化。   这里由于其数据量很少，不用像上面那道题目进行大量的数学推导，可直接在普通型母函数的基础上进行构造。

    我们不难构造出下面的指数型母函数。 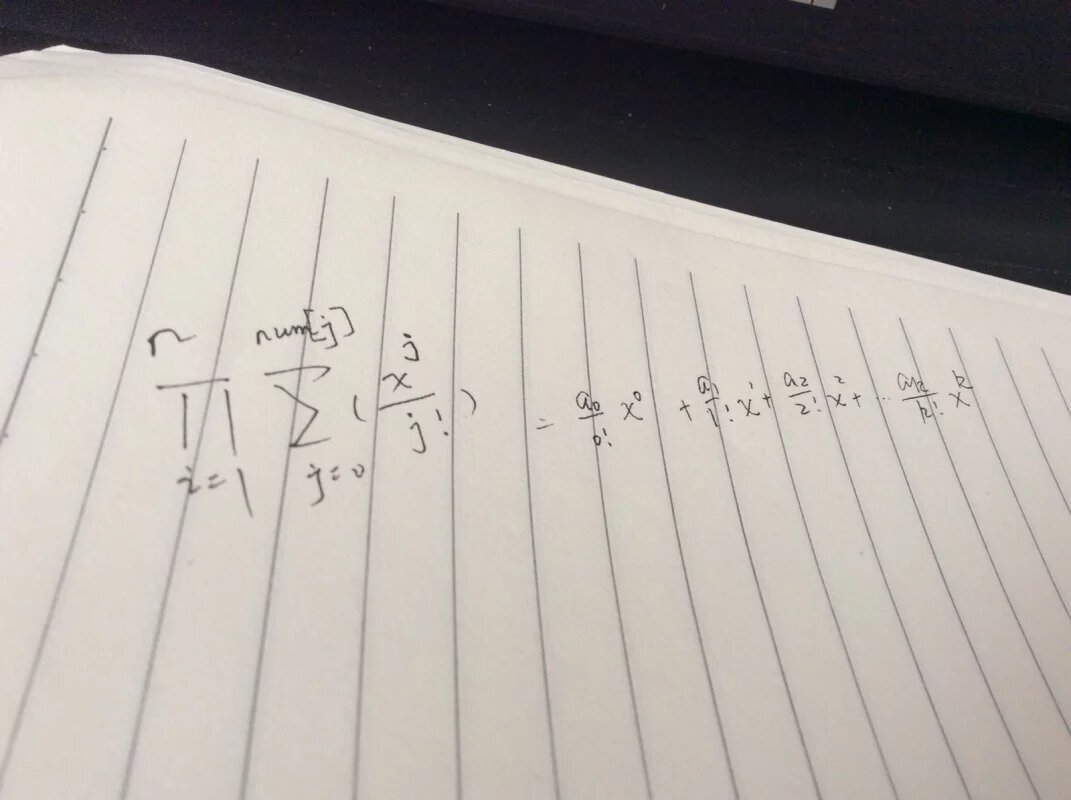     基于对普通型母函数编程实现的理解，这里发生的变化是有x^k变成了(x^k)/(k!)，这里只需在原有的基础上进行相应的调整即可。    注意到图中两个式子是指数型母函数的两种不同的表达方式，我们用左式构造程序，然后得到右式各个单项式的系数。注意这里的系数ak/k!表示含k个元素的组合数，想要排列数，输出ak即可，即在原有的结果上乘以对应数的阶乘。
  代码如下。

#include<stdio.h>
#include<string.h>

using namespace std;
int f[10];
void make_f()
{
     f[0] = 1 , f[1] = 1;
       for(int i = 2;i <= 10;i++)
              f[i] = f[i - 1] * i;
}
int main()
{
    int m , n;
    int num[15];
    double status[15] , dynamic[15];

    make_f();
    while(scanf("%d %d",&n , &m) != EOF)
    {
          for(int i = 1;i <= n ;i++)
              scanf("%d",&num[i]);
          memset(status , 0 , sizeof(status));
          memset(dynamic , 0, sizeof(dynamic));

          for(int i = 0;i <= num[1];i++)
               status[i] = 1.0/f[i];

          for(int i = 2;i <= n;i++)
          {
                for(int j = 0;j <= m;j++)
                {
                     for(int k = 0;k <= num[i] && k + j <= m;k++)
                              dynamic[k + j] += status[j] / f[k];
                }
                 memcpy(status , dynamic , sizeof(dynamic));
                 memset(dynamic , 0 , sizeof(dynamic));
          }

          printf("%.0lf
",status[m] * f[m]);
    }
}

 
    参考系《程序设立中的组合数学》