我们结合一个题目具体看看Catalan数的应用。(Pr0blem source:hdu2067)
Problem Description
小兔的叔叔从外面旅游回来给她带来了一个礼物,小兔高兴地跑回自己的房间,拆开一看是一个棋盘,小兔有所失望。不过没过几天发现了棋盘的好玩之处。从起点(0,0)走到终点(n,n)的最短路径数是C(2n,n),现在小兔又想如果不穿越对角线(但可接触对角线上的格点),这样的路径数有多少?小兔想了很长时间都没想出来,现在想请你帮助小兔解决这个问题,对于你来说应该不难吧!
Q3:1~n按照次序进栈,那么有多少种不同的出栈方案?
这里我们用二进制的思维去看这个问题。n个数字中,每个数字对应两种操作,入栈(记为1),出栈(记为0),那么所有的情况可以看成n个1和n个0的排列情况,即往2n位的二进制数中填充1、0,我们可以得到总方案数——C(2n,n),但是考虑到每个数字必须先入栈后出栈,势必存在不符合情况的组合,现在我们就要找到不符合情况的数量,然后再用总数量C(2n,n)减掉即可。
在不符合先入后出条件的情况中,势必会在二进制数的某个奇数位前(包含该奇数位),出现了m+1个0和m个1,此时该奇数位后(不包含该奇数位),有n-m-1个0和n-m个1。 此时我们再想这样一个模型,2n位二进制数含有n+1个0和n-1个1,由于这个2n位二进制数必定存在偶数位前(包含该偶数位),0比1多2,呢么就必定存在奇数位前(包含该奇数位),出现了m+1个0,m个1,这与上面的情况是对应的。而在这种情况下,该奇数位以后(不含该奇数位)有n-m-1个1和n-m个0,这里将1和0对调,刚好个上面的情况吻合起来,而方案数却没有改变,因此我们得出结论——不符合的方案数是C(2n,n-1)。 通过化简整理,出栈的总顺序为C(2n,n) - C(2n,n-1) = (1/n+1)*C(2n,n),这同时也是Catalan数递推式的解。
不妨来看一道关于出入栈方案数的题目(Problem source:hdu1023)
Problem Description
As we all know the Train Problem I, the boss of the Ignatius Train Station want to know if all the trains come in strict-increasing order, how many orders that all the trains can get out of the railway.
题目大意:就是n辆货车,他们进栈的顺序有多少种。 数理分析:这里轨道只有一条,这条轨道就模拟了Q3模型中的栈,而这里想求的其实就是一个顺序入栈而后不同次序出栈的方案数。 编程实现:组合数学中给出的计数公式随着n的扩大,数值一般会爆掉c/c++中的数据类型,于是这里为了解决大数问题,我们用JAVA的写法来实现。
参考代码如下。
import java.io.*; import java.util.*; import java.math.BigInteger; public class Main { public static void main(String args[]) { BigInteger[] a = new BigInteger[101]; a[0] = BigInteger.ZERO; a[1] = BigInteger.valueOf(1); for(int i = 2; i <= 100; ++i) a[i] = a[i - 1].multiply(BigInteger.valueOf(4 * i - 2)).divide(BigInteger.valueOf(i+1)); Scanner in = new Scanner(System.in); int n; while(in.hasNext()) { n = in.nextInt(); System.out.println(a[n]); } } }
既然在圆上有2n个点,那么我们可以找到一条直线将圆分成两部分A、B,这两各区域上面分别有n个点,我们任选一个区域A,任选一个点i,然后连接点i和区域B中的任意一个点j,此时圆又被分成区域C和区域D,我们这里就可以得到Q1中的递推式——h(n) = ∑h(k)h(n-k)。也就是说,对于2n个点在圆上两两连接,形成不相交线段的方案数,等于凸n+1边形分割成三角形的方案数,都是第n个Catalan数(根据其定义,Catalan数是有第0个的,即C[0] = 0)。
知道了这个模型本质上也是求解Catalan数,我们就来看一个相关的问题。(Problem source:hdu1134)
Problem Description
This is a small but ancient game. You are supposed to write down the numbers 1, 2, 3, ... , 2n - 1, 2n consecutively in clockwise order on the ground to form a circle, and then, to draw some straight line segments to connect them into number pairs. Every number must be connected to exactly one another. And, no two segments are allowed to intersect.
It's still a simple game, isn't it? But after you've written down the 2n numbers, can you tell me in how many different ways can you connect the numbers into pairs? Life is harder, right?
It's still a simple game, isn't it? But after you've written down the 2n numbers, can you tell me in how many different ways can you connect the numbers into pairs? Life is harder, right?
参考代码在上面给出代码的基础上进行稍稍的改动即可。
Q5:给点节点数n,我们用这n个节点能够生成多少个二叉树? 针对这个问题,我们还是基于上文一开始给出Catalan数的思维角度(Q1分割n边形的问题),同样,为了记数的方便和最终结论的他统一,这里我们来分析n+1个节点能够生成多少个二叉树。 既然是生成二叉树,其必含有根节点、左子树、右子树。这里除去根节点,左子树和右子树一共还有n个节点,我们假设左子树有k个节点,那么右子树就有n-k个节点,这里我们再假设h(n)表示n各节点对应的方案数,那么这种情况下二叉树不同的种类就有h(k) * h(n - k),那么再依次遍历k的值进行累加,我们就得到了递推式——h(n+1) = ∑h(k)h(n-k),这里k的范围是[0,n]。 这其实又回到了Q1所进行的推导。 最终我们可以得出结论,凸n+1边形分隔成三角形且对角线不相交的方案数,和n+1个节点形成二叉树的种类数是一样的,都对应第n个Catalan数。
让我们找一道相关的题目实践一下我们的结论。(Problem source:hdu1130)
Problem Description
A binary search tree is a binary tree with root k such that any node v reachable from its left has label (v) <label (k) and any node w reachable from its right has label (w) > label (k). It is a search structure which can find a node with label x in O(n log n) average time, where n is the size of the tree (number of vertices).
Given a number n, can you tell how many different binary search trees may be constructed with a set of numbers of size n such that each element of the set will be associated to the label of exactly one node in a binary search tree?
Given a number n, can you tell how many different binary search trees may be constructed with a set of numbers of size n such that each element of the set will be associated to the label of exactly one node in a binary search tree?
可以看到,这里的问题是和Q5一模一样的问题,这里只需编程实现Catalan数即可。
参考代码在上面给出代码是一致的。
Q6:小明住在市中心北n个街区,东n个街区,那么小明要穿越街区到市中心上班,有多少条路可以走?
仔细的读者可能已经发现,这道问题是和Q1下给出的问题是一模一样的,在上文中我们用动态规划的思想来找到二者的联系,而在这里,我们再用组合思维来分析它。
前奏一样,我们依然通过一条对角线将整个矩形划分成对称的了两块。这里我们把向左走记为+1,向下走记为-1,并且选择矩形的左上半区域。问题转换成n个+1和n个-1能够形成多少种序列。 由于不能越过对角线,即在满足要求的序列a1a2a3……ai……an中,必须有任意的k∈[1,n],是的a1+a2+a3……+ak >= 0。 至此我们发现,问题其实回到了出入栈顺序的问题,为了语言的简洁,这里不再重复证明。
那么让我们结合一个具体的问题。(Problem source : hdu 4165)
Problem Description
Aunt Lizzie takes half a pill of a certain medicine every day. She starts with a bottle that contains N pills.
On the first day, she removes a random pill, breaks it in two halves, takes one half and puts the other half back into the bottle.
On subsequent days, she removes a random piece (which can be either a whole pill or half a pill) from the bottle. If it is half a pill, she takes it. If it is a whole pill, she takes one half and puts the other half back into the bottle.
In how many ways can she empty the bottle? We represent the sequence of pills removed from the bottle in the course of 2N days as a string, where the i-th character is W if a whole pill was chosen on the i-th day, and H if a half pill was chosen (0 <= i < 2N). How many different valid strings are there that empty the bottle?
On the first day, she removes a random pill, breaks it in two halves, takes one half and puts the other half back into the bottle.
On subsequent days, she removes a random piece (which can be either a whole pill or half a pill) from the bottle. If it is half a pill, she takes it. If it is a whole pill, she takes one half and puts the other half back into the bottle.
In how many ways can she empty the bottle? We represent the sequence of pills removed from the bottle in the course of 2N days as a string, where the i-th character is W if a whole pill was chosen on the i-th day, and H if a half pill was chosen (0 <= i < 2N). How many different valid strings are there that empty the bottle?
题目大意:一个药罐子里有n片药,现在你从中取药,拿到整片(记作W),掰成两半,一半放回去,如果拿到半片(记作H),直接拿出来,需要我们计算的是直到把药罐里的药片全部拿走,有多少种方案。 数理分析:经过对题意的抽象,我们很容易认识到,实际上题目就是给出n个W和n个H,让我们计算长度为2n的可行序列数。 这里就回到了Q6的模型,或者说是出入栈顺序的模型,这里便不再累述。
参考代码也是同上然后做一点小小改动即可。
我们再来看一道关于Catalan数变形应用的问题。(Problem source : hdu 3723)
Problem Description
A delta wave is a high amplitude brain wave in humans with a frequency of 1 – 4 hertz which can be recorded with an electroencephalogram (EEG) and is usually associated with slow-wave sleep (SWS). -- from Wikipedia
The researchers have discovered a new kind of species called "otaku", whose brain waves are rather strange. The delta wave of an otaku's brain can be approximated by a polygonal line in the 2D coordinate system. The line is a route from point (0, 0) to (N, 0), and it is allowed to move only to the right (up, down or straight) at every step. And during the whole moving, it is not allowed to dip below the y = 0 axis.
For example, there are the 9 kinds of delta waves for N = 4: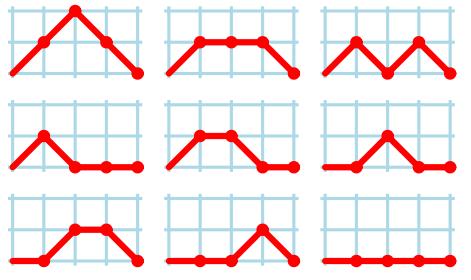
The researchers have discovered a new kind of species called "otaku", whose brain waves are rather strange. The delta wave of an otaku's brain can be approximated by a polygonal line in the 2D coordinate system. The line is a route from point (0, 0) to (N, 0), and it is allowed to move only to the right (up, down or straight) at every step. And during the whole moving, it is not allowed to dip below the y = 0 axis.
For example, there are the 9 kinds of delta waves for N = 4:

题目大意:在如图所示的坐标纸当中,给定一个数字n,问你从(0,0)到达(n,0)有多少条路可以走,每次移动x必须+1,y可以选择+1、-1、0。
数理分析:可以看到,这道题终点是(n,0),这就表明这n次操作中,对y的+1和-1操作数量是相同的,这就让我们联想到了上文中关于Catalan数的模型,无论是穿越街区、还是出入栈顺序的问题,都可以拿过来尽心对比。 但是仅仅知道了和Catalan数有关还是不行的,假设+1有k个,那么我们首先要做的就是在n步操作中选出2k个位置以填充+1和-1,我们这里假设序列T[n]是记录答案的序列,这里T[n] = C(n,2k) * Catalan[k]。考虑到n的取值,我们不好单独计算前面的组合数,所以我们将T[n]看成一个整体,通过数学推导看是否能得出新的齐次递推式子。
推导如下。


通过推导我们可以看到,我们得到了新的齐次递推式
import java.math.BigInteger; import java.util.Scanner; public class Main { public static void main(String[] args) { Scanner sc = new Scanner(System.in); BigInteger mod = BigInteger.TEN.pow(100); BigInteger sum = new BigInteger("0"); BigInteger t = new BigInteger("0"); while (sc.hasNext()) { int n = sc.nextInt(); sum = BigInteger.ONE; t = BigInteger.ONE; for(int k = 1; k + k <= n; k++) { t = t.multiply(BigInteger.valueOf((n-2*k+1)*(n-2*k+2))) .divide(BigInteger.valueOf(k*(k+1))); sum = sum.add(t); } System.out.println(sum.mod(mod)); } } }
我们继续来看一道有关Catalan数的问题(Prblem sourece:hdu 1133)
Problem Description
The "Harry Potter and the Goblet of Fire" will be on show in the next few days. As a crazy fan of Harry Potter, you will go to the cinema and have the first sight, won’t you?
Suppose the cinema only has one ticket-office and the price for per-ticket is 50 dollars. The queue for buying the tickets is consisted of m + n persons (m persons each only has the 50-dollar bill and n persons each only has the 100-dollar bill).
Now the problem for you is to calculate the number of different ways of the queue that the buying process won't be stopped from the first person till the last person. Note: initially the ticket-office has no money.
The buying process will be stopped on the occasion that the ticket-office has no 50-dollar bill but the first person of the queue only has the 100-dollar bill.
Suppose the cinema only has one ticket-office and the price for per-ticket is 50 dollars. The queue for buying the tickets is consisted of m + n persons (m persons each only has the 50-dollar bill and n persons each only has the 100-dollar bill).
Now the problem for you is to calculate the number of different ways of the queue that the buying process won't be stopped from the first person till the last person. Note: initially the ticket-office has no money.
The buying process will be stopped on the occasion that the ticket-office has no 50-dollar bill but the first person of the queue only has the 100-dollar bill.
题目大意:就是有m个人拿50元,n个人拿100元,他们通过自动取票机买一张50元的票,但是你这个取票机是空的,问你有多少种方案,是的这m+n个人可以都得到票。 数理分析:如果m<n,是没有符合要求的方案数的,这显而易见。如果这里是2n个人,n个50块n个100块,那么这就是很典型诶对Catalan数的模型了,它的分析思路很类似关于出入栈顺序的模型。但是这里,还是有一定的区别的,但是我们可以用相同的思想进行分析。
这里我们依然往出入栈顺序的那个模型上靠拢。我们是用间接法,符合要求的方案数= 总方案数量 - 不符要求方案数。
这里对于总方案数很好说,C(m+n,m)orC(m+n,n)都是可以的。 对于不符合要求的方案数,我们就采取和分析出入栈顺序一样的方法(详情可以往上翻),我们将50元和100元分别转化成1、0,这样我们就相当于计算不同种数的01序列,那么在m+n位的01序列中,我们分析不符合要求的情况,其一定在k位,之前出现了r位1和r+1位0,那么在剩下的m+n-k位中,则有m-r个1和n-r-1个0,这里我们将m+n-k位中的0换成1,1换成0,则相当于在m+n位二进制数中填充m+1个0,这种情况下的方案数是等价于变化(后m+n-k位的0->1,1->0)之前的方案数,即不符合要求的方案数。
考虑到实际情况,每个人是不同的,所以需要在分别再乘以m和n的阶乘。 通过以上分析,我们得知,符合方案数的的计算公式——(C(m+n,m) - C(m+n,m+1))*m!*n!。 接下来便是推导出便于编程实现的式子(展开组合公式)。 化简的最终结果——(m+n)!*(m-n+1)/(m+1)。
参考代码如下。
import java.util.*; import java.math.BigInteger; public class Main{ public static void main(String[] args){ int a,b; Scanner in=new Scanner(System.in); int cnt=0; while(in.hasNext()){ cnt++; a=in.nextInt(); b=in.nextInt(); BigInteger ans=BigInteger.ONE; if(a==0&&b==0)break; if(a<b) ans=BigInteger.ZERO; else { for(int i=1;i<=a+b;i++){ ans=ans.multiply(BigInteger.valueOf(i)); } int mpl=(a-b+1); int dvd=(a+1); ans=ans.multiply(BigInteger.valueOf(mpl)); ans=ans.divide(BigInteger.valueOf(dvd)); } System.out.println("Test #"+cnt+":"); System.out.println(ans); } } }
参考系:《组合数学》Richard