聚类试图将数据集中的样本划分为若干个通常不相交的子集，每个子集称为一个“簇”。通常为“无监督学习”，对无标记训练样本学习来揭示数据的内在规律和性质。
下面主要讲三种聚类模型：
1. 原型聚类
“原型”是指样本空间中具有代表性的点。通常是算法先对原型进行初始化，然后对原型进行迭代更新求解。介绍三种著名的原型聚类方法。
（1）k均值算法：贪心策略来求解（而不是最小化能量函数）
k均值算法是最简单的一种聚类算法。算法的目的是使各个样本与所在类均值的误差平方和达到最小（这也是评价K-means算法最后聚类效果的评价标准），给定样本集
，簇划分为
，最小化平方误差：
是簇Ci的均值向量，E值越小则簇内样本相似度越高。最小化上面那个式子为NP-hard问题，所以k均值算法用了贪心策略通过迭代优化来求解。
算法的步骤如下：
输入：样本集D，聚类簇数k.
1. 初始化。从D中随机选择k个样本作为初始均值向量{μ1,μ2,...,μk}
2. 进行迭代。根据相似度准则将样本集中数据分配到最接近的聚类中心，从而形成一类。
3. 更新聚类中心。然后以每一类的平均向量作为新的聚类中心，重新分配数据对象。
4. 反复执行第二步和第三步直至满足中止条件。
（2）学习向量量化（有监督学习）
“学习向量量化”（简称LVQ）假设数据样本带有类别标记，学习过程利用样本的监督信息来辅助聚类。给定样本集D={(x1,y1),(x2,y2),...,(xm,ym)}，每个样本xj是由n个属性描述的特征向量(xj1,xj2,...,xjn)，yj属于Y是样本xj的类别标记。LVQ的目标是学得一组n维原型向量{p1,p2,...,pq}，每个原型向量代表一个聚类簇，簇标记ti属于Y，其中簇标记ti可以是一样的，例如：5个原型向量p1,p2,...,p5对应的类别标记为c1,c2,c2,c1,c1.
算法步骤如下：
1. 初始化。样本集D={(x1,y1),(x2,y2),...,(xm,ym)}；原型向量个数为q，各原型向量预设的类别标记{t1,t2,...,tq}；学习率η在(0,1)区间。例如：对第q个簇可从类别标记为tq的样本中随机选取一个作为原型向量。
2. 迭代优化。算法随机选取一个有标记的样本，找出与其距离最近的原型向量，并根据两者的类别标志是否一致来对原型向量进行相应的更新。
从样本集 D 随机选取样本(xj,yj)，计算样本 xj 与 pi (1≤i≤q)的距离，找出最近的 pi*；
若 yj=ti*类别相同，p'=pi* + η(xj-pi*)
反之，p'=pi* - η(xj-pi*)
将原型向量pi*更新为 p'
学习率η在(0,1)区间，若类别标记相同，使得原型向量pi*在更新为p'之后更接近xj；若类别标记不同，使得原型向量pi*在更新为p'之后远离xj。
3. 重复2直到满足停止条件。
（3）高斯混合聚类
采用概率模型来表达聚类原型，GMM和k-means很像，简单地说，k-means的结果是每个数据点被分配到其中一个cluster了，而GMM则给出这些点被分配到每个cluster的概率，又称作soft assignment。
首先回顾一下多元高斯分布的定义，对n维样本空间中的随机向量x，若 x 服从高斯分布，其概率密度函数定义为：
将概率密度函数记为p(x|μ,∑)，我们可定义高斯混合分布：
该分布由k个混合成分组成，每个混合成分对应一个高斯分布，这里的k相当于将样本分为k个cluster。μi,∑i是第i个高斯混合成分的参数，αi>0为相应的“混合系数”。
假设样本的生成过程由高斯混合分布给出：首先根据α1，α2，...，αk定义的先验分布选择高斯混合成分，其中αi为选择第i个混合成分的概率；然后根据被选择的混合成分的概率密度函数进行采样，从而生成相应的样本。
若训练集D={x1,x2,...,xm}由上述过程生成，令随机变量zj属于{1,2,...,k}表示生成样本xj的高斯混合成分，其取值未知，P(zj)为先验概率。显然，zj的先验概率P(zj=i)对应于αi(i=1,2,...,k)，即先验概率就是属于第k个混合成分的概率。根据贝叶斯定理，zj的后验概率分布对应于：
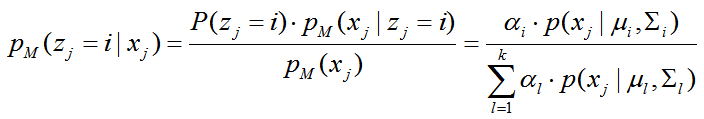它给出了样本xj由第i个高斯混合成分生成的后验概率，为方便叙述，将其简记为
，当高斯混合分布已知时，高斯混合聚类将把样本集D划分为k个簇 C={C1,C2,...,Ck}，每个样本 xj 的簇标记为
，簇的划分由原型对应的后验概率确定。
我们需要确定高斯混合模型参数。想法是，找到这样一组参数，它所确定的概率分布生成这些给定的数据点的概率最大，显然，给定样本集D，可采用极大似然估计。通常单个点的概率都很小，许多很小的数字相乘起来在计算机里很容易造成浮点数下溢，因此我们通常会对其取对数。
常采用EM算法进行迭代优化求解。下面做一个简单的推导。
若参数{(αi,μi,∑i)|1≤i≤k}能使似然函数最大化，则让其对μi求偏导为0，有
相应的，对∑i求偏导为0得：
对于混合系数αi，除了要最大化LL(D)，还需满足αi≥0，∑αi=1，考虑拉格朗日形式 LL(D)+λ(∑αi-1)，λ为拉格朗日乘子，对αi的导数为0，有
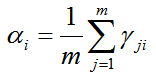
由上述推导即可获得高斯混合模型的EM算法：在每步迭代中，先根据当前参数来计算每个样本属于每个高斯成分的后验概率γji（E步），再根据上面的式子更新{(αi,μi,∑i)|1≤i≤k}（M步）
高斯混合聚类算法如下：
（1）初始化高斯混合分布的模型参数
（2）EM算法迭代更新
（3）迭代完参数确定后可得到后验概率，根据高斯混合分布确定簇划分，将每个样本划分到相应的簇，根据。
2. 密度聚类
参考：http://www.cnblogs.com/CBDoctor/archive/2011/10/24/2222358.html
《机器学习》，周志华著