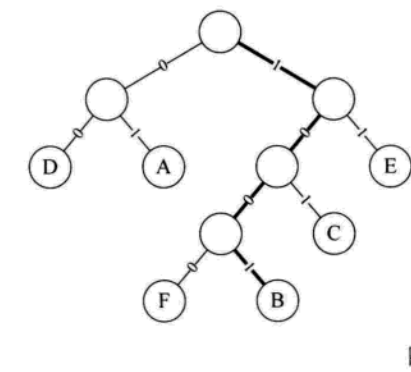
先来看一下书中给二叉树的定义:
-

-
对于二叉树的一些基本特点这里就不多说了
接下来,介绍一些比较特殊的二叉树:
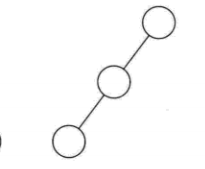
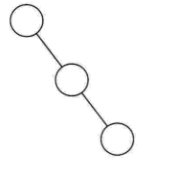
- 斜树:所有结点都只有左子树的叫左斜树,所有结点都只有右子树的叫右斜树
- 满二叉树:除叶结点外的所有的结点都存在做孩子和右孩子
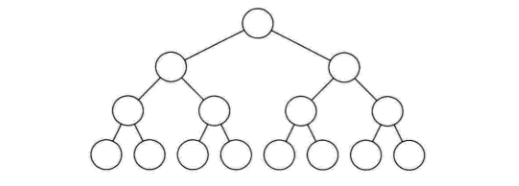
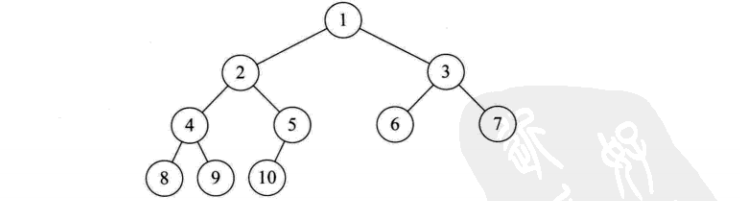
- 完全二叉树:对一个二叉树从高到低,从左到右进行编号,若该二叉树与同样深度的满二叉树各个结点的编号对应一致,则该二叉树为完全二叉树
然后,看一些二叉树的基本性质:
-
性质一:二叉树在第i层上至多有2^(i-1)个结点 //因为根结点是第1层而不是第0层,因此是i-1,根据二叉树的定义即可得知此条性质
-
性质二:深度为k的二叉树至多有2^k-1个结点 //根据数学归纳法即可得知此条性质,列举k值,然后观察,很容易得出结论
-
性质三:对于一个二叉树,若叶子结点数为N0,度为2的结点数为N2,则N0=N2+1
- 证明:假设度为1的结点数为N1,总结点数为N,则N=N0+N1+N2,又根据孩子结点求和得N=N0×0+N1×1+N2×2+1(根结点),两等式相连即可得:N0=N2+1
-
二叉树性质四:具有n个结点的完全二叉树的深度为[log2]n+1 //[x]表示不大于x的最大整数
- 注:求解深度的话我通常都是直接使用2^n进行迭代测试,比计算log方便,也不容易出错,但在程序中还是使用log比较简洁和清楚
二叉树的存储结构:
- 顺序存储:使用一维数组即可实现,然而适用性不强
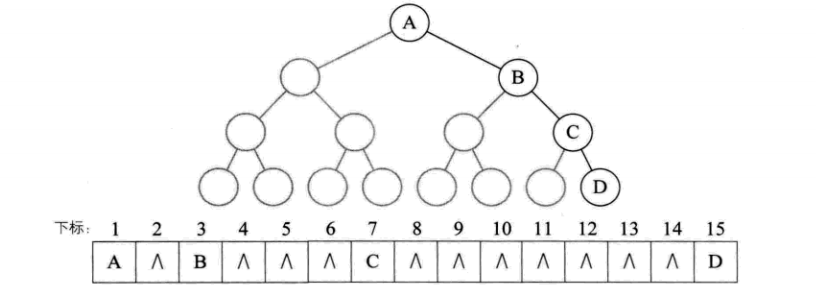
- 二叉链表:
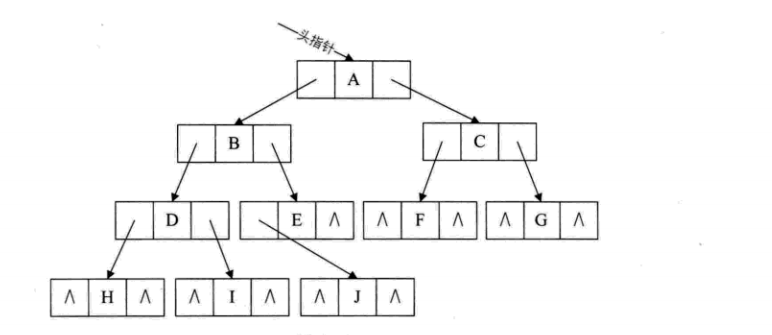
遍历二叉树:
- 书中定义:

-
遍历方法:
- 前序遍历
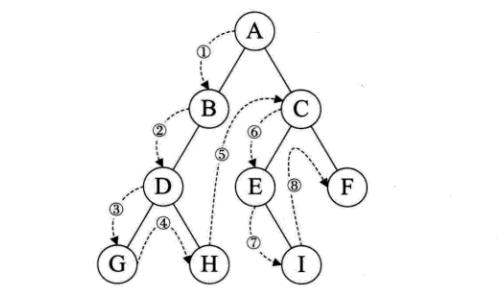
- 中序遍历
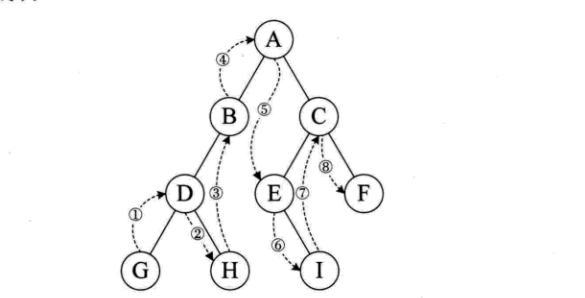
- 后序遍历
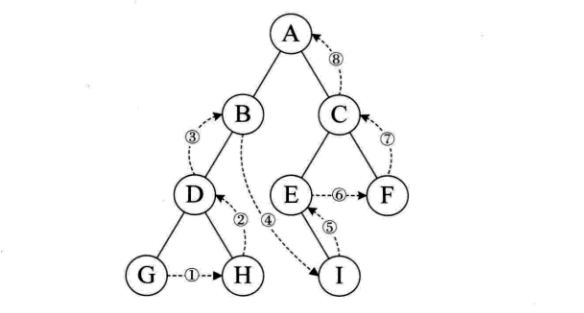
- 层次遍历
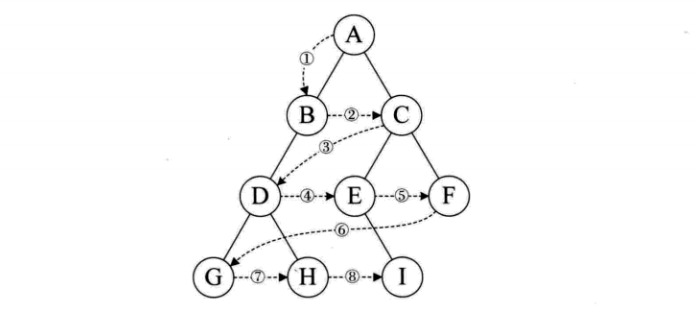
- 前序遍历
线索二叉树:将空指针指中的左孩子域指向前驱,右孩子域指向后继
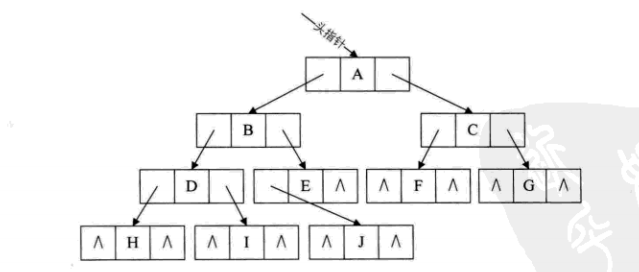
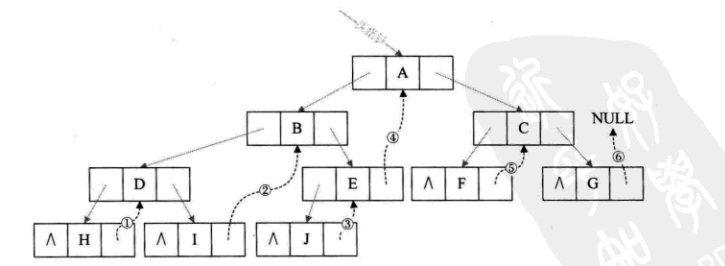
- 上面一张图中有一个很大的缺点就是你无法判断一个结点的左孩子域到底是左孩子还是前驱,右孩子域到底是右孩子还是后继,因此有了以下改进的版本:
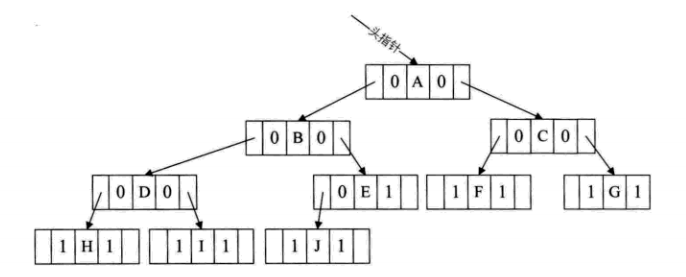
- 树、二叉树、森林之间的相互转化
赫夫曼树:主要是路径图,最优树的相关概念;统计数据中各字符出现的频率,构造赫夫曼树,使路径最短,这是数据压缩的基本原理