OO——JML作业总结

目录

• 第三单元博客作业
  • JML语言理论基础
    • 1.注释结构
    • 2.JML表达式
      • 2.1 原子表达式
      • 2.2 量化表达式
      • 2.3 集合表达式
      • 2.4 操作符
    • 3.方法规格
    • 4.类型规格
  • 应用工具链
  • JMLUnitNG使用实例
  • 作业架构设计
    • 第一次作业
    • 第二次作业
    • 第三次作业
  • BUG与修复
  • 规格撰写和理解上的心得体会

第三单元博客作业

JML语言理论基础

1.注释结构

JML以javadoc注释的方式来表示规格，每行都以@起头。有两种注释方式，和普通的java语言的注释类似，分为行注释和块注释。

• 行注释：//@abbitation
• 块注释：/*@ annotation @*/

按照javadoc习惯，JML注释一般被放在被注释成分的近邻上部。

2.JML表达式

JML表达式是对Java表达式的扩展，新增了一些操作符和原子表达式。同样JML表达式中的操作符也有优先级的概念。在JML断言中，不可以使用带有赋值语义的操作符，如++, --, +=等操作符，因为这样的操作符会对被限制的相关变量的状态进行修改，产生副作用。

2.1 原子表达式

esult表达式

表示一个非void类型的方法执行所获得的结果，即方法执行后的返回值。 esult表达式的类型就是方法声明中定义的返回值类型

old(expr)表达式

用来表示一个表达式expr在相应方法执行前的取值。该表达式涉及到评估expr中的对象是否发生变化，遵从Java的引用规则，即针对一个对象引用而言，只能判断引用本身是否发生变化，而不能判断引用所指向的对象实体内容是否发生变化。

ot_assigned(x, y, ...)表达式

用来表示括号中的变量是否在方法执行过程中被赋值。如果没有被赋值，返回为true，否则返回为false。用于后置条件的约束。

ot_modified(x, y, ...)表达式

与上面的not_assigned表达式类似，该表达式限制括号中的变量在方法执行期间的取值未发生变化。

onnullelements(container)表达式

表示container对象中存储的对象不会有null。

ype(type)表达式

返回类型type对应的类型(Class)。

typeof(expr)表达式

该表达式返回expr对应的准确类型。

2.2 量化表达式

forall表达式

全称两次修饰的表达式，表示对于给定范围内的元素，每个元素都满足相应的约束。

exists表达式

存在量词修饰的表达式，表示对于给定范围内的元素，存在某个元素满足相应的约束。

sum表达式

返回给定范围内的表达式的和。

product表达式

返回给定范围内的表达式的连乘结果。

max表达式

返回给定范围内的表达式的最大值。

min表达式

返回给定范围内的表达式的最小值。

um_of表达式

返回指定变量中满足相应条件的取值个数。

2.3 集合表达式

可以在JML规格中构造一个局部的集合（容器），明确集合中可以包含的元素。

2.4 操作符

子类型关系操作符：E1 < E2

如果类型E1是E2的子类型，则表达式的结果为真，否则为假。如果E1和E2是相同的类型，该表达式的结果也为真。

等价关系操作符：b_expr1<==>b_expr2

推理操作符：b_expr1==>b_expr2

变量引用操作符：

othing表示一个空集，everything表示一个全集，即包括当前作用域下能够访问到的所有变量。

3.方法规格

前置条件(pre-condition)

前置条件通过requires子句来表示：requires P;。其中requires是JML关键词，表达的意思是“要求调用者确保P为真”。注意，方法规格中可以有多个requires子句，是并列关系，即调用者必须同时满足所有的并列子句要求。如果设计者想要表达或的逻辑，则应该使用一个requires子句，在其中的谓词P中使用逻辑或操作符来表示相应的约束场景：requires P1||P2;。

后置条件(post-condition)

后置条件通过ensures子句来表示：ensures P;。其中ensures是JML关键词，表达的意思是“方法实现者确保方法执行返回结果一定满足谓词P的要求，即确保P为真”。同样，方法规格中可以有多个ensures子句，是并列关系，即方法实现者必须同时满足有所并列ensures子句的要求。如果设计者想要表达或的逻辑，这应该在在一个ensures子句中使用逻辑或(||)操作符来表示相应的约束场景：ensures P1||P2;。

副作用范围限定(side-effects)

副作用指方法在执行过程中会修改对象的属性数据或者类的静态成员数据，从而给后续方法的执行带来影响。从方法规格的角度，必须要明确给出副作用范围。JML提供了副作用约束子句，使用关键词ssignable或者modifiable。

signal子句

signals子句的结构为signals (***Exception e) b_expr，意思是当b_expr为true时，方法会抛出括号中给出的相应异常e。对于上面的例子而言，只要输入满足z<0，就一定会抛出异常IllegalArgumentException。需要注意的是，所抛出的既可以是Java预先定义的异常类型，也可以是用户自定义的异常类型。此外，还有一个注意事项，如果一个方法在运行时会抛出异常，一定要在方法声明中明确指出（使用Java的throws表达式），且必须确保signals子句中给出的异常类型一定等同于方法声明中给出的异常类型，或者是后者的子类型。

4.类型规格

不变式invariant

不变式（invariant）是要求在所有可见状态下都必须满足的特性，语法上定义invariant P，其中invariant为关键词，P为谓词。对于类型规格而言，可见状态(visible state)是一个特别重要的概念。下面所述的几种时刻下对象o的状态都是可见状态：

• 对象的有状态构造方法（用来初始化对象成员变量初值）的执行结束时刻
• 在调用一个对象回收方法(finalize方法)来释放相关资源开始的时刻
• 在调用对象o的非静态、有状态方法(non-helper)的开始和结束时刻
• 在调用对象o对应的类或父类的静态、有状态方法的开始和结束时刻
• 在未处于对象o的构造方法、回收方法、非静态方法被调用过程中的任意时刻
• 在未处于对象o对应类或者父类的静态方法被调用过程中的任意时刻

状态变化约束constraint

对象的状态在变化时往往也许满足一些约束，这种约束本质上也是一种不变式。JML为了简化使用规则，规定invariant只针对可见状态(即当下可见状态)的取值进行约束，而是用constraint来对前序可见状态和当前可见状态的关系进行约束。

应用工具链

jmlrac

jmlrac runs a Java(TM) program, named in the FQClassName argument, that has been compiled using the JML runtime assertion checker compiler jmlc. It provides the program access to classes in the org.jmlspecs.jmlunit, org.jmlspecs.models, and org.jmlspecs.jmlrac.runtime packages. It also provides access to runtime assertion checked version of interfaces in the J2SDK libraries (e.g., in java.lang and java.util).

jmlc

SelfTest is a small set of Java annotation types along with an annotation processor (refer to API specifications).

openjml

OpenJML is a program verification tool for Java programs that allows you to check the specifications of programs annotated in the Java Modeling Language.

jmlunit/jmlunitNG

For each Java(TM) or JML source file, and for the top-level class or interface defined in that source file with the name of the source file, the commmand jmlunit, or the graphical user interface version jmlunit-gui , generates code for an abstract test oracle class, that can be used to test that class or interface with JUnit.

JMLUnitNG使用实例

首先感谢伦佬在讨论区里面的分享，我是参照着讨论区实现的。

首先创建一个demo文件夹，在里面有Demo.java文件

demo
└── Demo.java

0 directories, 1 file

然后执行

./jmlunitng demo/Demo.java

生成后的文件树

demo/
├── Demo.java
├── Demo_InstanceStrategy.java
├── Demo_JML_Data
│   ├── ClassStrategy_int.java
│   ├── ClassStrategy_java_lang_String.java
│   ├── ClassStrategy_java_lang_String1DArray.java
│   ├── compare__int_lhs__int_rhs__0__lhs.java
│   ├── compare__int_lhs__int_rhs__0__rhs.java
│   └── main__String1DArray_args__10__args.java
├── Demo_JML_Test.java
├── PackageStrategy_int.java
├── PackageStrategy_java_lang_String.java
└── PackageStrategy_java_lang_String1DArray.java

1 directory, 12 files

下面进行编译

javac -cp jmlunitng.jar demo/*/*.java
javac -cp jmlunitng.jar demo/Demo_JML_Test.java
./openjml -rac demo/Demo.java

测试

java -cp jmlunitng-1_4.jar demo.Demo_JML_Test

结果

[TestNG] Running:
  Command line suite

Passed: racEnabled()
Passed: constructor Demo()
Passed: static compare(-2147483648, -2147483648)
Failed: static compare(0, -2147483648)
Failed: static compare(2147483647, -2147483648)
Passed: static compare(-2147483648, 0)
Passed: static compare(0, 0)
Passed: static compare(2147483647, 0)
Failed: static compare(-2147483648, 2147483647)
Passed: static compare(0, 2147483647)
Passed: static compare(2147483647, 2147483647)
Passed: static main(null)
Passed: static main({})

===============================================
Command line suite
Total tests run: 13, Failures: 3, Skips: 0
===============================================

对于生成样例的分析

// demo/Demo.java
package demo;

public class Demo {
    /*@ public normal_behaviour
      @ ensures 
esult == lhs - rhs;
    */
    public static int compare(int lhs, int rhs) {
        return lhs - rhs;
    }

    public static void main(String[] args) {
        compare(114514,1919810);
    }
}

可见Demo.java里面在main函数里面调用了compare方法，通过观察TestNG生成的样例，可以看到会用身份极端的数据对其进行测试，包括空集合、int的上下限这样的数据。

作业架构设计

第一次作业

结构分析

对于第一次作业，整体上的层次比较简单。Main作为主类，通过AppRunner.newInstance()调用MyPath和MyPathContainer两个类。

MyPath主要是用来对路径中的结点进行管理。在内部没有改变路境内结点的方法，也就是说每个Path在创建完成后就不能被改变。因为像getNode(int)这样的方法需要根据索引来获得路径中的结点，所以需要一个ArrayList容器来保存路径的顺序。但是当结点的个数比较多的时候，仅有一个ArrayList容器会大大提高containsNode(int)方法的复杂度，故这里采用冗余设计的思想，新建了HashSet容器，在构造函数中一起初始化，这样就可以降低containsNode(int)方法的复杂度。

MyPathContainer作为路径的容器，其中包含了对容器进行路径删减的方法，以remove方法来举例，由于路径本身和路径的内容在容器中都是唯一的，所以在这个类中既有通过Pathid来删除路径，也有通过Path删除路径，所以我建立了两个ArrayList容器，一个用来存储路径，一个用来存储路径Id。在第一次作业的过程中，我只是关注了distincNodeCount方法的复杂度降低问题，所以我对于路径和标号没有建造HashSet容器来降低访问的复杂度。

为了降低distincNodeCount方法的复杂度，我建立了一个HashMap，里面结点作为键，结点在路径容器中出现的次数作为值，这样只需要判断HashMap有多少个键就可以得到路径容器中不同结点的个数。

复杂度和依赖度分析

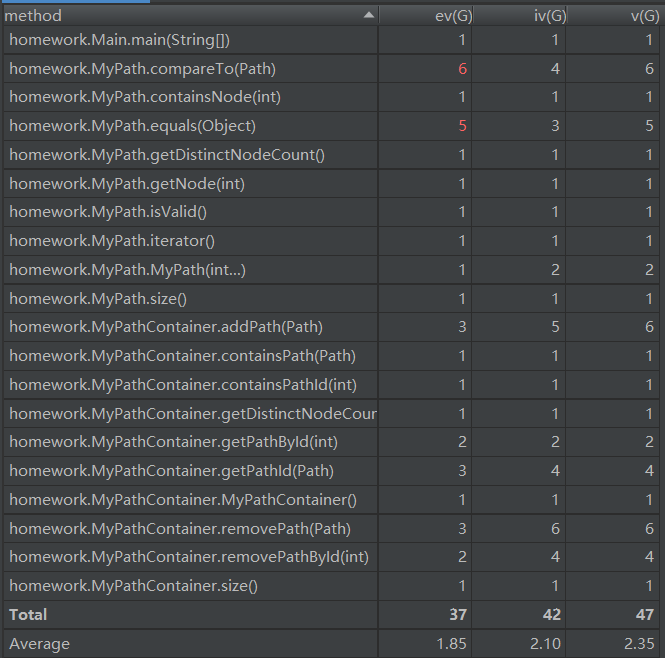
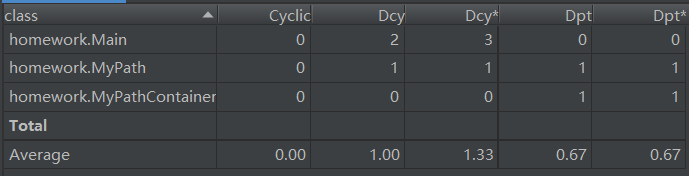
整体上来看，第一次作业由于结构比较的简单，所以复杂度和依赖度总体上处于一个比较合理的状态，但是我们也可以看到compareTo(Path)和equals(Object)两个方法的ev(G)异常。

public boolean equals(Object obj) {
        boolean res = true;
        if (obj instanceof Path) {
            if (nodes.size() != ((Path) obj).size()) {
                return false;
            }
            for (int i = 0; i < nodes.size(); i++) {
                if (nodes.get(i) != ((Path) obj).getNode(i)) {
                    res = false;
                    break;
                }
            }
            return res;
        } else {
            return false;
        }
    }

对于equals方法，由于我们是按照规格对两个路径进行比较，采用的是字典序，这设计到了对路径的遍历，所以提高了复杂度。

public int compareTo(Path o) {
        int minSize = Math.min(size(), o.size());
        for (int i = 0; i < minSize; i++) {
            if (nodes.get(i) < o.getNode(i)) {
                return -1;
            } else if (nodes.get(i) == o.getNode(i)) {
                continue;
            } else {
                return 1;
            }
        }
        if (size() < o.size()) {
            return -1;
        } else if (size() == o.size()) {
            return 0;
        } else {
            return 1;
        }
    }

这里的compareTo方法真的是一个败笔，我采用了一种很麻烦的实现，在第二次作业中我对这个方法进行了改进，在这就不多说了，真的是傻。

第二次作业

结构分析

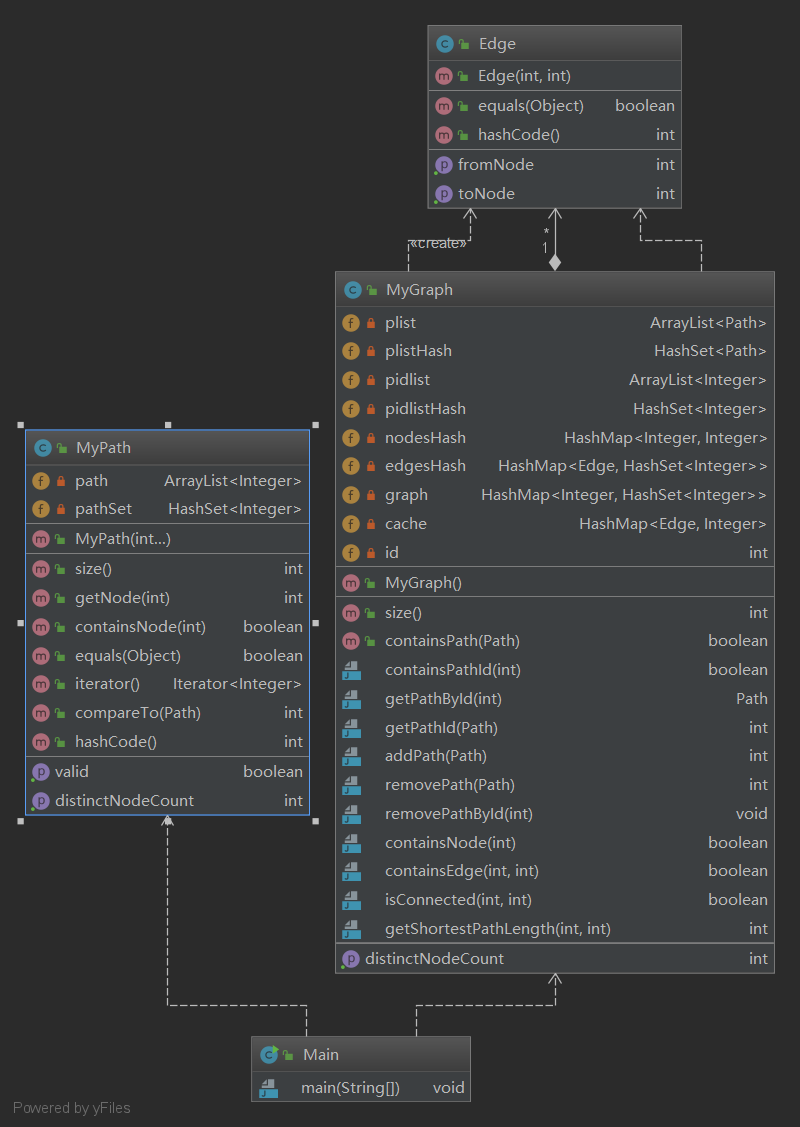
从图中我们可以看到，在第二次作业中，我没有进行继承，MyPath和MyGraph两个类中的很多部分都是直接从上一次作业中复制过来。当时在做作业的时候想到这一次的代码不至于超过标准行数，所以说也就没有采用继承了。

但是，我对第一次作业进行了一部分的重构。首先是MyPath，对于像size()，containsNode(int)这两个方法，我改成了对HashSet进行访问，原先对ArrayList进行访问的复杂度较高，有可能在MyPathContainer里进行调用的时候忽略这个问题而导致整个函数的时间复杂度超标，最终TLE。其次，我简化了一下compareTo()函数。

对于MyPathContainer，在本次作业中添加了三个读的方法，由于评测有CPU时间的限制，我在这里通过构造荣誉容器和把复杂度分散给add和remove两类方法的方式，使得新增的读方法的复杂度大大降低。由于第二次作业中有对边的操作，所以我构造了一个Edge类，用来表示边。

我新增了plistHash和pidlistHash两个容器，来降低像containsPath和containsPathId这样的方法的时间复杂度。此外，我新增了edgesHash容器，以边作为键，包含这条边的路径Id的集合作为值，这样以来，在containsEdges方法中只需要判断edgesHash容器中是否含有这个边就可以。

graph是一个HashMap类型的图的邻接表表示，因为在isConnected()和getShortestPathLength两个方法中我才用了BFS的方式寻找最短路径。cache在这里是一个缓存的作用，里面保存着已经计算过的两点之间的最短路径，只有当使用add和remove方法对路径进行删减之后，才会对这个缓存进行更新。

复杂度和依赖度分析

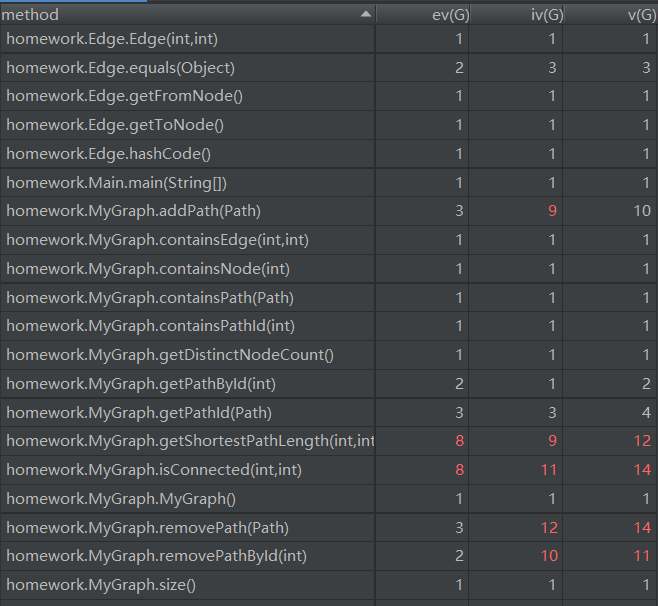
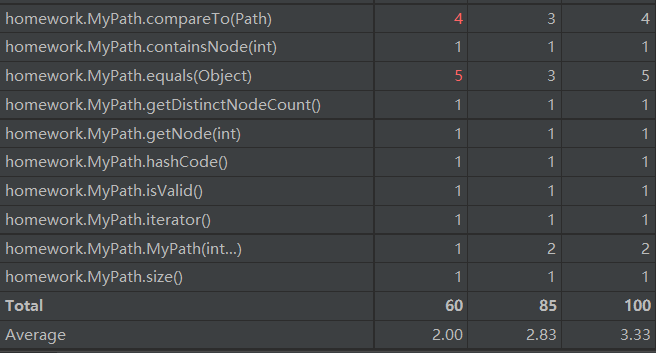
从图中可以看到在本次作业中，明显的高复杂度方法就是addPath，removePath，removePathById以及isConnected和getShortestPathLength。

add和remove两个类型的方法，主要是因为在添加和删除路径的时候，需要对大量的容器进行增删，来保证不同容器所表达的信息之间的一致性，在这个地方就不免的会有循环的嵌套以及大量if分支的使用，为此我也在这三个函数上花费了大量的时间去调试。下面给出一部分代码片段，相信大家也就不难理解了。

if (edgesHash.containsKey(temp)) {
                HashSet<Integer> tempValue;
                tempValue = edgesHash.get(temp);
                if (tempValue.contains(pathId)) {
                    tempValue.remove(pathId);
                    if (tempValue.isEmpty()) {
                        edgesHash.remove(temp);
                        if (graph.containsKey(temp.getFromNode())) {
                            tempValue = graph.get(temp.getFromNode());
                            tempValue.remove(temp.getToNode());
                            if (!tempValue.isEmpty()) {
                                graph.put(temp.getFromNode(), tempValue);
                            } else {
                                graph.remove(temp.getFromNode());
                            }
                        }
                        if (graph.containsKey(temp.getToNode())) {
                            tempValue = graph.get(temp.getToNode());
                            tempValue.remove(temp.getFromNode());
                            if (!tempValue.isEmpty()) {
                                graph.put(temp.getToNode(), tempValue);
                            } else {
                                graph.remove(temp.getToNode());
                            }
                        }
                    } else {
                        edgesHash.put(temp, tempValue);
                    }
                }
            }

而对于isConnected和getShortestPathLength两个方法，在里面用到了BFS广度优先遍历，所以导致了内部出现了循环嵌套，增加了复杂度。

while (!now.isEmpty()) {
                res += 1;
                for (int node : now) {
                    if (node == toNodeId) {
                        cache.put(edge, res);
                        return true;
                    } else {
                        visited.add(node);
                    }
                }
                HashSet<Integer> temp = new HashSet<>();
                for (int node1 : now) {
                    for (int node2 : graph.get(node1)) {
                        if (!visited.contains(node2)) {
                            temp.add(node2);
                        }
                    }
                }
                now = temp;
            }

第三次作业

结构分析

在第三次作业中，我进行了进一步的重构。首先由于这一次作业又增加了几个方法，所以一个类显然已经不能够在合法的范围内完成这么多的功能，所以这一次我的MyRailwaySystem类继承了MyGraph类，在新的MyRailwaySystem我只是实现了本次作业新增的方法。

对于MyGraph类，我在这一次作业中进行的最主要的改动就是增添了一个powerGraph容器，这里面是通过邻接表的方式保存的拆点之后的图。它的增添和删减工作也同样是在add和remove两类方法中完成。因为在本次作业中，需要进行有权图的最短路径的查找，上一次作业的BFS我没有想到来处理这个问题的方法，所以经过向大佬们的询问，我在这一次作业采用了拆点+Dijsktra的方式。

Node类是本次作业新增的类，实际上就是对结点的一个封装，由于拆点的需要，对于每一个结点我们不仅仅要知道它的值，还需要知道它所在的路径，所以在这个地方对此进行封装。

QueueCon类是在使用Dijkstra算法的时候需要的。

复杂度和依赖度分析

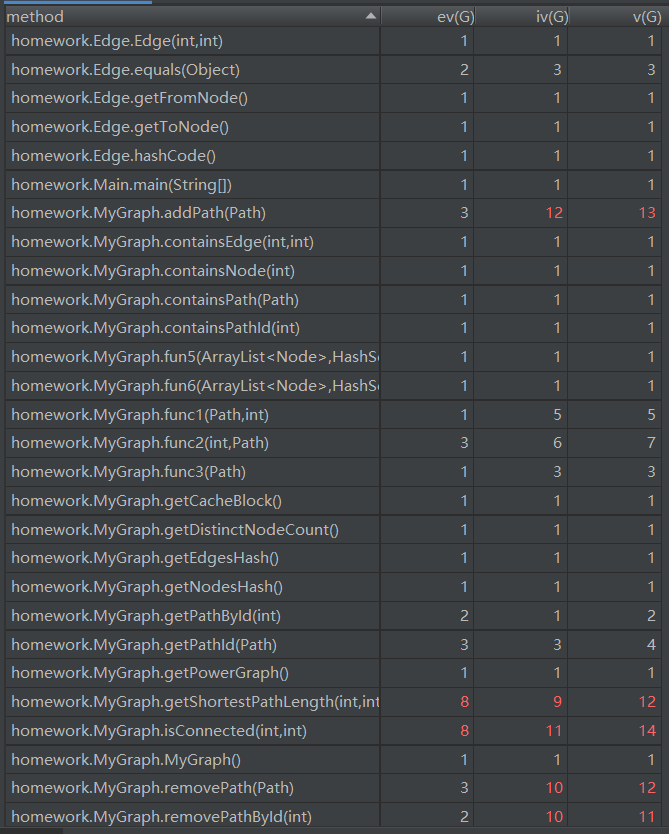
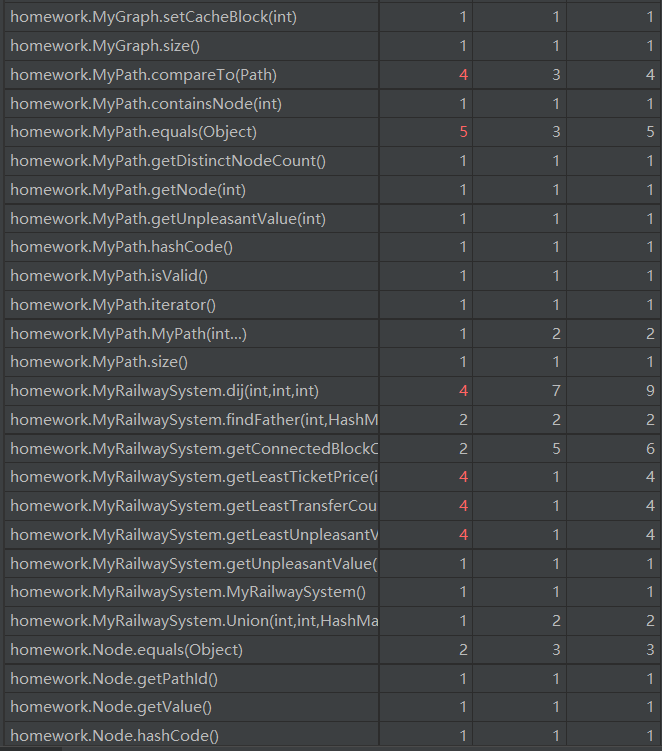
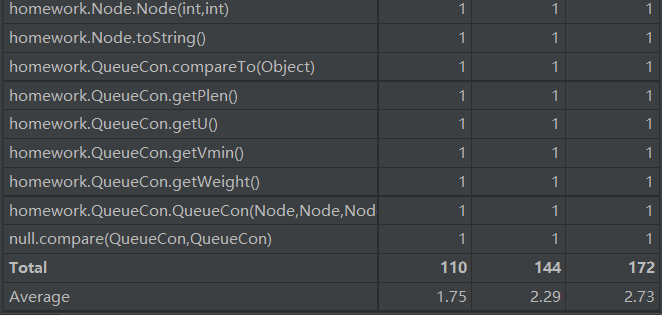
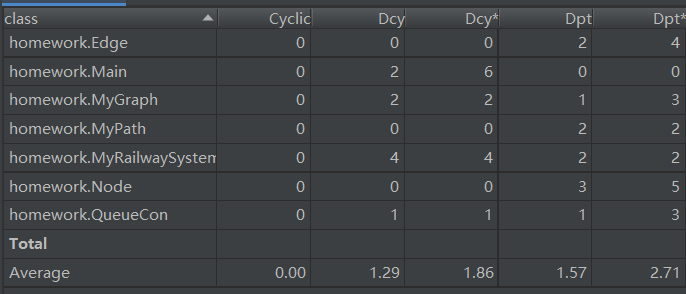
由于新增了一些容器，所以add和remove两类方法的复杂度有所提高。对于本次作业，我们可以从图中看到新增的几个方法复杂度较高都是因为用到了dij这个方法的缘故

public int dij(int fromNodeId, int toNodeId, int type) {
        if (fromNodeId == toNodeId) {
            return 0;
        }
        int vnum = super.getPowerGraph().size();
        HashMap<Node, ArrayList<Node>> paths = new HashMap<>();
        int count = 0;
        Queue<QueueCon> cands = new PriorityQueue<>();
        QueueCon temp4 = new QueueCon(new Node(0, -1),
                new Node(fromNodeId, 0), new Node(fromNodeId, 0));
        cands.add(temp4);
        while (count < vnum && !cands.isEmpty()) {
            QueueCon temp5 = cands.poll();
            Node plen = temp5.getPlen();
            Node u = temp5.getU();
            Node vmin = temp5.getVmin();
            if (paths.containsKey(vmin)) {
                continue;
            }
            ArrayList<Node> temp = new ArrayList<>();
            temp.add(u);
            temp.add(plen);
            paths.put(vmin, temp);
            for (ArrayList<Node> temp2 : super.getPowerGraph().get(vmin)) {
                Node v = temp2.get(0);
                Node w = temp2.get(type);
                if (!paths.containsKey(v)) {
                    QueueCon temp3 = new QueueCon(new Node(plen.getValue()
                            + w.getValue(), -1), v, vmin);
                    cands.add(temp3);
                }
            }
            count += 1;
        }
        Node end = new Node(toNodeId, 0);
        ArrayList<Node> now = paths.get(end);
        int res = 0;
        if (type == 1) {
            res = now.get(1).getValue() - 2;
        } else if (type == 2) {
            res = now.get(1).getValue() - 1;
        } else {
            res = now.get(1).getValue() - 32;
        }
        
        return res;
    }

这个方法是进行最短路径的查询，可以从代码中很轻易的看到里面有循环的嵌套。

BUG与修复

第一次作业

在第一次作业中，我的BUG发生在两个remove方法中，代码如下

public int removePath(Path path) throws PathNotFoundException {
        if (path != null && path.isValid()) {
            if (containsPath(path)) {
                int index = plist.indexOf(path);
                plist.remove(index);
                for (int node: path) {
                    int value = nodesHash.get(node) - 1;
                    if (value > 0) {
                        nodesHash.put(node, value); // 一开始在这里value - 1了
                    } else {
                        nodesHash.remove(node);
                    }
                }
                return pidlist.remove(index);
            } else {
                throw new PathNotFoundException(path);
            }
        } else {
            throw new PathNotFoundException(path);
        }
    }

没错，就是很无语，一时手误，导致了强测挂点，但是我认为这是由于我的课下测试不充分导致的。在第二次作业和第三次作业中，我才用了JUnit来进行单元测试，通过这种方式保证了每一部分函数的正确性。

第三次作业

对于第三次作业的BUG，我在这里就不贴代码了，TLE和RE，大家应该都懂得。至于为什么会这样，在强测爆炸之后，我阅读自己的代码，发现自己的Dij写成了$O(n^n)$，呵呵，也是无语了，都怪自己数据结构太菜，在BUG修复阶段我改进了Dij，然后再WSL上time java发现2s左右就跑完了......

规格撰写和理解上的心得体会

JML作为一种对Java程序进行规格化设计的一种表示语言，很好的描述了一个方法或类的功能以及约束等等，相对于自然语言，JML减少了二义性，避免了不同的人的语言描述差异带来的理解上的偏差。

对于规格的撰写，两次的实验课给我留下了很深的印象，对我来说规格撰写最困难的就是，到底写到什么样的程度才算合适。在这两次实验中，每次我都是对规格进行一次又一次的添加，虽然有一些规格我自己认为是描述清楚了或者暗含着其他的约束，但是我就担心阅读的人可能不会注意到这一点，所以我的规格写的都是比较多的。

对于规格的理解，我认为还是有一定难度的，尤其是当规格十分复杂的时候。比如在第三次作业中，为了规格的描述，添加了一些不需要实现的函数，在没有文字的说明的情况下，直接阅读这些规格十分困难。比如：

/*@ requires containsPath(path) && 0 <= fromIndex && fromIndex < toIndex && toIndex < path.size();
      @ ensures (exists int[] mred; mred[0] == fromIndex && mred[mred.length - 1] == toIndex && mred.length <= (toIndex - fromIndex) && (forall int i; 0 <= i && i < mred.length - 1; path.containsEdge(path.getNode(mred[i]), path.getNode(mred[i + 1])));
      @           (forall int[] red; red[0] == fromIndex && red[red.length - 1] == toIndex && red.length <= (toIndex - fromIndex) && (forall int i; 0 <= i && i < red.length - 1; path.containsEdge(path.getNode(red[i]), path.getNode(red[i + 1]))) &&
      @                       getUnpleasantValue(path, mred) <= getUnpleasantValue(path, red)) && 
esult == getUnpleasantValue(path, mred));
      @*/

对于第三次作业中的一些函数，我如果不和同学们进行讨论的话，我估计自己是很难做出来的。