迪杰斯特拉(Dijkstra)算法
是求从某个源点到其余各顶点的最短路径,即对已知图 G=(V,E),给定源顶点 s∈V,找出 s 到图中其它各顶点的最短路径。
我总结下核心算法,伪代码如下:
Dijkstra() { 初始化Dist、Path、final // 每次求得v0到某顶点v的最短路径 while (图的顶点数-1) { 1. 找到非最短路径顶点集中距V0最近的顶点v 得到其顶点下标和距离 将v加入到最短距离顶点集合中 打印相关内容 2. 依次修改其它未得到最短路径顶点的Dist[k]值 假设求得最短路径的顶点为u, 则 Dist[k] =min( Dist[k], Dist[u] + G.arcs[u][k] ) 同时修改Path[k]:Path[k] = Path[u] +G.vex[k] } }
实例:

源代码:
1 #include <iostream> 2 #include <stdio.h> 3 #include <stdlib.h> 4 #include <string> 5 using namespace std; 6 7 #define MAX_VERTEX_NUM 100 8 #define MAX_EDGE_NUM 200 9 #define MAX_VERTEX_NAMELEN 100 10 #define INF 65535 11 12 typedef struct{ 13 char name[MAX_VERTEX_NAMELEN]; 14 }VerType; 15 16 // 图的邻接矩阵存储结构 17 typedef struct{ 18 int VertexNum,EdgeNum; // 顶点数,边数 19 VerType Vertex[MAX_VERTEX_NUM]; // 顶点集 20 int Edge[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 边集 21 }MGragh; 22 23 // 邻接矩阵建图 24 void CreateMGragh(MGragh *Gra) 25 { 26 int i,j,k,w; 27 char v1[MAX_VERTEX_NAMELEN],v2[MAX_VERTEX_NAMELEN]; 28 29 printf("请输入顶点数及边数(顶点数 边数) "); 30 scanf("%d %d%*c",&(Gra->VertexNum),&(Gra->EdgeNum)); 31 32 printf("请输入顶点信息 "); 33 for (i=0; i<Gra->VertexNum; i++){ 34 printf("%d.",i+1); 35 gets(Gra->Vertex[i].name); 36 } 37 38 // 初始化邻接矩阵 39 for (i=0; i<Gra->VertexNum; i++){ 40 for (j=0; j<Gra->VertexNum; j++){ 41 if (i==j){ 42 Gra->Edge[i][j] = 0; // 各点到自己的距离为0 43 } 44 else{ 45 Gra->Edge[i][j] = INF; // 各点到不相邻的点距离为无穷 46 } 47 } 48 } 49 50 printf("请输入边信息(顶点,顶点,权值) "); 51 for (i=0; i<Gra->EdgeNum; i++){ 52 printf("%d.",i+1); 53 scanf("%[^,]%*c%[^,]%*c%d%*c",v1,v2,&w); 54 55 for (j=0; j<Gra->VertexNum; j++){ 56 for (k=0; k<Gra->VertexNum; k++){ 57 if (strcmp(Gra->Vertex[j].name,v1) == 0 && strcmp(Gra->Vertex[k].name,v2) == 0){ 58 Gra->Edge[j][k] = w; 59 } 60 } 61 } 62 } 63 } 64 65 int Dist[MAX_VERTEX_NUM]; // 存储VO到各点的最短路径的权值和 66 string ShortPath[MAX_VERTEX_NUM]; // 存储V0到各点的最短路径 67 68 void ShortPathByDijkstra(MGragh *Gra,int vo) 69 { 70 printf(" 最短路径为: "); 71 int v,w,k,min; 72 int final[MAX_VERTEX_NUM]; // final[w]=1 表示已经求得顶点V0到Vw的最短路径 73 74 // 初始化数据 75 for (v=0; v<Gra->VertexNum; v++){ 76 final[v] = 0; // 全部顶点初始化为未找到最短路径 77 Dist[v] = Gra->Edge[vo][v]; // 将与vo点有连线的顶点加上权值 78 if (Dist[v] != INF && Dist[v] != 0){ 79 ShortPath[v] += Gra->Vertex[vo].name; 80 ShortPath[v] += Gra->Vertex[v].name; 81 } 82 else{ 83 ShortPath[v] = ""; 84 } // 记录由V0连出去的边的路径 如AB、AC 85 } 86 Dist[vo] = 0; // v0到自己的路径为0 87 final[vo] = 1; // 标记已经找到v0到自己的最短路径 88 89 // 每次求得vo到某顶点V的最短路径 90 for (v=1; v<Gra->VertexNum; v++){ 91 min = INF; 92 93 // 将某点加入最短路径顶点集 94 for (w=0; w<Gra->VertexNum; w++){ 95 if (final[w] == 0 && Dist[w]<min){ 96 k = w; 97 min = Dist[w]; 98 } 99 } // 找到非最短路径顶点集中距V0最近的顶点 得到其顶点下标和距离 100 final[k] = 1; // 将目前找到最近的顶点置1 即将该点加入最短路径顶点集 101 printf("%d ",Dist[k]); 102 cout << ShortPath[k] << endl; 103 104 // 修正当前最短路径及距离 105 for (w=0; w<Gra->VertexNum; w++){ 106 // 如果经过v顶点的路径比现在这条路径的长度短的话就更新 107 if (final[w] == 0 && (min+Gra->Edge[k][w]) < Dist[w]){ 108 Dist[w] = min + Gra->Edge[k][w]; 109 ShortPath[w] = ShortPath[k]; 110 ShortPath[w] += Gra->Vertex[w].name; 111 } 112 } 113 } 114 } 115 116 int main() 117 { 118 MGragh g; 119 CreateMGragh(&g); 120 ShortPathByDijkstra(&g,0); 121 return 0; 122 }
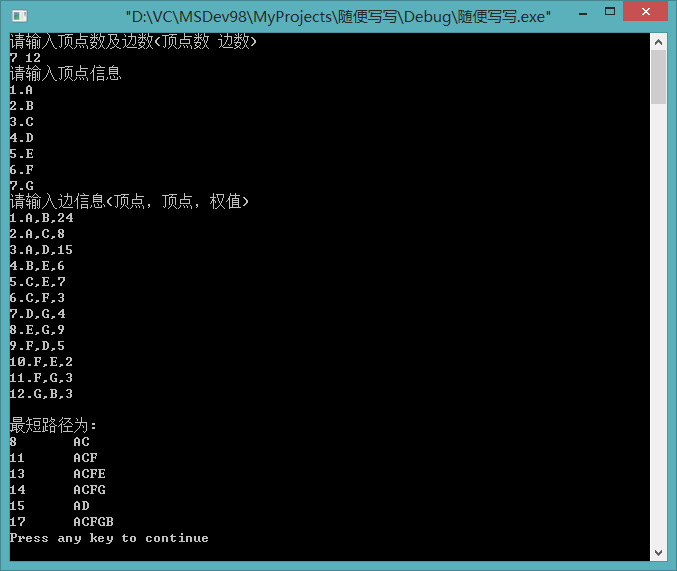
测试用例及结果: