Silverlight开发历程—（绘制矢量图之Polyline 和 Polygon）

 Polyline(多线段) 和 Polygon（多边形）

 Polyline(多线段) 和 Polygon（多边形）是Silverlight中简单但功能强大的绘图对象。它允许你声明N个Points属性值，然后根据Points属性的坐标先后顺序来绘制图形，并且支持线条内部的颜色填充。

首先介绍一下PolyLine，他比Line元素更加强大，下面例子利用Polyline来绘制线条：

<Polyline Stroke="Black" Points="0,0 50,50 300,0 400,100"></Polyline>

运行结果：

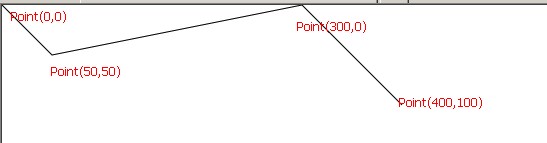
代码中Points="0,0 50,50 300,0 400,100“ 总共分成了四对坐标然后根据四个点来绘制图形。

下面的例子来 说明Polyline(多线段) 和 Polygon（多边形）两个的用法和区别

        <!-- 三组坐标组成的PolyLine开放图形-->
        <Polyline Stroke="Blue" StrokeThickness="6" Points="50,50 150,200 300,50" Fill="Gold"></Polyline>

        <!-- 三组坐标组成的Polygon封闭图形-->
        <Polygon Stroke="Blue" StrokeThickness="6" Points="400,50 650,200 800,50" Fill="Gold"></Polygon>

运行结果：

上面例子分别利用Polyline(多线段) 和 Polygon（多边形）来绘制图型，然后除了坐标了不一样，其它的基本上都相同并且都填充了相同的颜色，唯一区别是

我们利用Polygon绘制出来的图形是一个封闭的图形。

Polyline(多线段) 和 Polygon（多边形）均具有FillRule（填充规则）使用FillRule可以声明线条内的填充规则。如下面的例子：

<StackPanel x:Name="LayoutRoot" Background="White" Orientation="Horizontal">
                <!--EvenOdd 确定一个点是否位于填充区域内的规则，具体方法是从该点沿任意方向画一条无限长的射线，
                    然后计算该射线在给定形状中因交叉而形成的路径段数。 如果此数目为奇数，则该点在内部；如果是偶数，则该点在外部。  
            Nonzero 确定一个点是否位于路径填充区域内的规则，具体方法是从该点沿任意方向画一条无限长的射线，然后检查形状段与该射线的交点。
                    从零开始计数，每当线段从左向右穿过该射线时加 1，而每当路径段从右向左穿过该射线时减 1。 
                    计算交点的数目后，如果结果为零，则说明该点在路径外部。 否则，说明该点位于路径内部。-->

        <Polygon Stroke="Blue" StrokeThickness="2" Fill="Orange" Margin="120,0,60,0" FillRule="EvenOdd"
                 Points="15,200 68,70 110,200 0,125 134,125"></Polygon>

        <Polygon Stroke="Blue" StrokeThickness="2" Fill="Red" Margin="50,0,0,0" FillRule="Nonzero"
                 Points="15,200 68,70 110,200 0,125 134,125"></Polygon>
    </StackPanel>

运行结果：

分别使用了FillRule的两种规结果也不一样。