机器学习：支持向量机识别手写英文字母 SMO算法实现二元分类器

本文只构建一个能够识别一种英文符号的SVM，在此选择了C字符。

一、SVM构建

import numpy as np

class SMO:
    def __init__(self, C, tol, kernel='rbf', gamma=None):
        # 惩罚系数
        self.C = C
        # 优化过程中alpha步进阈值
        self.tol = tol

        # 核函数
        if kernel == 'rbf':
            self.K = self._gaussian_kernel
            self.gamma = gamma
        else:
            self.K = self._linear_kernel

    def _gaussian_kernel(self, U, v):
        '''高斯核函数'''
        if U.ndim == 1:
            p = np.dot(U - v, U - v)
        else:
            p = np.sum((U - v) * (U - v), axis=1)
        return np.exp(-self.gamma * p)
    
    def _linear_kernel(self, U, v):
        '''线性核函数'''
        return np.dot(U, v)

    def _g(self, x):
        '''函数g(x)'''
        alpha, b, X, y, E = self.args

        idx = np.nonzero(alpha > 0)[0]
        if idx.size > 0:
            return np.sum(y[idx] * alpha[idx] * self.K(X[idx], x)) + b[0]
        return b[0]

    def _optimize_alpha_i_j(self, i, j):
        '''优化alpha_i, alpha_j'''
        alpha, b, X, y, E = self.args
        C, tol, K = self.C, self.tol, self.K

        # 优化需有两个不同alpha
        if i == j:
            return 0

        # 计算alpha[j]的边界
        if y[i] != y[j]:
            L = max(0, alpha[j] - alpha[i])
            H = min(C, C + alpha[j] - alpha[i])
        else:
            L = max(0, alpha[j] + alpha[i] - C)
            H = min(C, alpha[j] + alpha[i])

        # L == H 时已无优化空间(一个点).
        if L == H:
            return 0

        # 计算eta
        eta = K(X[i], X[i]) + K(X[j], X[j]) - 2 * K(X[i], X[j])
        if eta <= 0:
            return 0

        # 对于alpha非边界, 使用E缓存. 边界alpha, 动态计算E.
        if 0 < alpha[i] < C:
            E_i = E[i]
        else:
            E_i = self._g(X[i]) - y[i]

        if 0 < alpha[j] < C:
            E_j = E[j]
        else:
            E_j = self._g(X[j]) - y[j]
        
        # 计算alpha_j_new
        alpha_j_new = alpha[j] +  y[j] * (E_i - E_j) / eta

        # 对alpha_j_new进行剪辑
        if alpha_j_new > H:
            alpha_j_new = H
        elif alpha_j_new < L:
            alpha_j_new = L
        alpha_j_new = np.round(alpha_j_new, 7)

        # 判断步进是否足够大
        if np.abs(alpha_j_new - alpha[j]) < tol * (alpha_j_new + alpha[j] + tol):
            return 0

        # 计算alpha_i_new
        alpha_i_new = alpha[i] + y[i] * y[j] * (alpha[j] - alpha_j_new)
        alpha_i_new = np.round(alpha_i_new, 7)

        # 计算b_new
        b1 = b[0] - E_i 
                -y[i] * (alpha_i_new - alpha[i]) * K(X[i], X[i]) 
                -y[j] * (alpha_j_new - alpha[j]) * K(X[i], X[j])

        b2 = b[0] - E_j 
                -y[i] * (alpha_i_new - alpha[i]) * K(X[i], X[j]) 
                -y[j] * (alpha_j_new - alpha[j]) * K(X[j], X[j])

        if 0 < alpha_i_new < C:
            b_new = b1
        elif 0 < alpha_j_new < C:
            b_new = b2
        else:
            b_new = (b1 + b2) / 2

        # 更新E缓存
        # 更新E[i],E[j]. 若优化后alpha若不在边界, 缓存有效且值为0.
        E[i] = E[j] = 0
        # 更新其他非边界alpha对应的E[k]
        mask = (alpha != 0) & (alpha != C)
        mask[i] = mask[j] = False
        non_bound_idx = np.nonzero(mask)[0]
        for k in non_bound_idx:
            E[k] += b_new - b[0] + y[i] * K(X[i], X[k]) * (alpha_i_new - alpha[i]) 
                                 + y[j] * K(X[j], X[k]) * (alpha_j_new - alpha[j])

        # 更新alpha_i, alpha_i
        alpha[i] = alpha_i_new
        alpha[j] = alpha_j_new

        # 更新b
        b[0] = b_new

        return 1

    def _optimize_alpha_i(self, i):
        '''优化alpha_i, 内部寻找alpha_j.'''
        alpha, b, X, y, E = self.args

        # 对于alpha非边界, 使用E缓存. 边界alpha, 动态计算E.
        if 0 < alpha[i] < self.C:
            E_i = E[i]
        else:
            E_i = self._g(X[i]) - y[i]

        # alpha_i仅在违反KKT条件时进行优化.
        if (E_i * y[i] < -self.tol and alpha[i] < self.C) or 
                (E_i * y[i] > self.tol and alpha[i] > 0):
            # 按优先级次序选择alpha_j.

            # 分别获取非边界alpha和边界alpha的索引
            mask = (alpha != 0) & (alpha != self.C)
            non_bound_idx = np.nonzero(mask)[0]
            bound_idx = np.nonzero(~mask)[0]

            # 优先级(-1)
            # 若非边界alpha个数大于１, 寻找使得|E_i - E_j|最大化的alpha_j.
            if len(non_bound_idx) > 1:
                if E[i] > 0:
                    j = np.argmin(E[non_bound_idx])
                else:
                    j = np.argmax(E[non_bound_idx])

                if self._optimize_alpha_i_j(i, j):
                    return 1

            # 优先级(-2)
            # 随机迭代非边界alpha
            np.random.shuffle(non_bound_idx)
            for j in non_bound_idx:
                if self._optimize_alpha_i_j(i, j):
                    return 1

            # 优先级(-3)
            # 随机迭代边界alpha
            np.random.shuffle(bound_idx)
            for j in bound_idx:
                if self._optimize_alpha_i_j(i, j):
                    return 1

        return 0

    def train(self, X_train, y_train):
        '''训练'''
        m, _ = X_train.shape

        # 初始化向量alpha和标量b
        alpha = np.zeros(m)
        b = np.zeros(1)

        # 创建E缓存
        E = np.zeros(m)

        # 将各方法频繁使用的参数收集到列表, 供调用时传递.
        self.args = [alpha, b, X_train, y_train, E]

        n_changed = 0
        examine_all = True
        while n_changed > 0 or examine_all:
            n_changed = 0

            # 迭代alpha_i
            for i in range(m):
                if examine_all or 0 < alpha[i] < self.C:
                    n_changed += self._optimize_alpha_i(i)

            print('n_changed: %s' % n_changed)
            print('sv num: %s' % np.count_nonzero((alpha > 0) & (alpha < self.C)))

            # 若当前迭代非边界alpha, 且没有alpha改变, 下次迭代所有alpha.
            # 否则, 下次迭代非边界间alpha.
            examine_all = (not examine_all) and (n_changed == 0)

        # 训练完成后保存模型参数: 
        idx = np.nonzero(alpha > 0)[0]
        # 1.非零alpha 
        self.sv_alpha = alpha[idx] 
        # 2.支持向量, 
        self.sv_X = X_train[idx]
        self.sv_y = y_train[idx]
        # 3.b.
        self.sv_b = b[0]

    def _predict_one(self, x):
        '''对单个输入进行预测'''
        k = self.K(self.sv_X, x)
        return np.sum(self.sv_y * self.sv_alpha * k) + self.sv_b

    def predict(self, X_test):
        '''预测'''
        y_pred = np.apply_along_axis(self._predict_one, 1, X_test)
        return np.squeeze(np.where(y_pred > 0, 1., -1.))

二、数据集加载与变换

http://archive.ics.uci.edu/ml/machine-learning-databases/letter-recognition/

import numpy as np
X=np.genfromtxt('F:/python_test/data/letter-recognition.data',delimiter=',',usecols=range(1,17))
print(X)
print(X.shape)

y=np.genfromtxt('F:/python_test/data/letter-recognition.data',delimiter=',',usecols=0,dtype=np.str)
print(y)
y=np.where(y == 'C',1,-1)
print(y)

 三、训练模型

#选择惩罚系数，步长阈值，核函数，高斯核函数的gamma（绝对带宽大小）
clf=SMO(C=1,tol=0.01,kernel='rbf',gamma=0.01)
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
clf.train(X_train,y_train)
from sklearn.metrics import accuracy_score
y_pred=clf.predict(X_test)
accuracy=accuracy_score(y_test,y_pred)
print(accuracy)

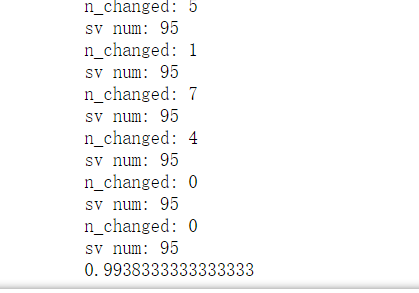
虽然准确度达到了0.99，但是要明确数据集中的C大约是由5%，全部预测成-1都会有95%的准确度，所以可以观察一下把C分类混淆矩阵

可以发现没有将一个不是C的字符认为是C，将37个C认为是其他字符。总体准确度还需要调参来提高

from sklearn.metrics import confusion_matrix
C=confusion_matrix(y_test,y_pred)
print(C)

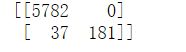
混淆矩阵

四、调节超参数的组合来提高SVM分类的质量

acc_list=[]
p_list=[]

#超参数列表，这里设置几个粗略的值
c_list=[0.1,1,5,10,15,20]
gamma_list=[0.1,0.2,0.3,0.4,0.5]
for C in c_list:
    for gamma in gamma_list:
        clf=SMO(C=C,tol=0.01,kernel='rbf',gamma=gamma)
        
        #训练预测并且计算精确度
        clf.train(X_train,y_train)
        y_pred=clf.predict(X_test)
        accuracy=accuracy_score(y_test,y_pred)
        
        #保存精确度以及相应的参数
        acc_list.append(accuracy)
        p_list.append((C,gamma))
        
idx=np.argmax(acc_list)
print(p_list(idx))

最后可以自己查看在那种情况下分类结果最好

clf=SMO(C=5,tol=0.01,kernel='rbf',gamma=0.05)
clf.train(X_train,y_train)
y_pred=clf.predict(X_test)
accuracy=accuracy_score(y_test,y_pred)
print(accuracy)