机器学习：朴素贝叶斯分类器实现二分类（伯努利型） 代码+项目实战

一、朴素贝叶斯分类器的构建

import numpy as np

class BernoulliNavieBayes:

    def __init__(self, alpha=1.):
        # 平滑系数, 默认为1(拉普拉斯平滑).
        self.alpha = alpha

    def _class_prior_proba_log(self, y, classes):
        '''计算所有类别先验概率P(y=c_k)'''

        # 统计各类别样本数量
        c_count = np.count_nonzero(y == classes[:, None], axis=1) 
        # 计算各类别先验概率(平滑修正)
        p = (c_count + self.alpha) / (len(y) + len(classes) * self.alpha)
       
        return np.log(p)

    def _conditional_proba_log(self, X, y, classes):
        '''计算所有条件概率P(x^(j)|y=c_k)的对数'''

        _, n = X.shape
        K = len(classes)

        # P_log: 2个条件概率的对数的矩阵
        # 矩阵P_log[0]存储所有log(P(x^(j)=0|y=c_k))
        # 矩阵P_log[1]存储所有log(P(x^(j)=1|y=c_k))
        P_log = np.empty((2, K, n))

        # 迭代每一个类别c_k
        for k, c in enumerate(classes):
            # 获取类别为c_k的实例
            X_c = X[y == c]
            # 统计各特征值为1的实例的数量
            count1 = np.count_nonzero(X_c, axis=0)
            # 计算条件概率P(x^(j)=1|y=c_k)(平滑修正)
            p1 = (count1 + self.alpha) / (len(X_c) + 2 * self.alpha)
            # 将log(P(x^(j)=0|y=c_k))和log(P(x^(j)=1|y=c_k))存入矩阵
            P_log[0, k] = np.log(1 - p1) 
            P_log[1, k] = np.log(p1) 

        return P_log

    def train(self, X_train, y_train):
        '''训练模型'''

        # 获取所有类别
        self.classes = np.unique(y_train)
        # 计算并保存所有先验概率的对数
        self.pp_log = self._class_prior_proba_log(y_train, self.classes)
        # 计算并保存所有条件概率的对数
        self.cp_log = self._conditional_proba_log(X_train, y_train, self.classes)

    def _predict(self, x):
        '''对单个实例进行预测'''

        K = len(self.classes)
        p_log = np.empty(K)

        # 分别获取各特征值为1和0的索引
        idx1 = x == 1
        idx0 = ~idx1

        # 迭代每一个类别c_k
        for k in range(K):
            # 计算后验概率P(c_k|x)分子部分的对数.
            p_log[k] = self.pp_log[k] + np.sum(self.cp_log[0, k][idx0]) 
                                    + np.sum(self.cp_log[1, k][idx1])

        # 返回具有最大后验概率的类别
        return np.argmax(p_log)

    def predict(self, X):
        '''预测'''

        # 对X中每个实例, 调用_predict进行预测, 收集结果并返回.
        return np.apply_along_axis(self._predict, axis=1, arr=X)

二、数据集的获取

http://archive.ics.uci.edu/ml/machine-learning-databases/spambase/

三、加载数据与数据转换

import numpy as np
data=np.loadtxt('F:/python_test/data/spambase.data',delimiter=',')
print(data)
X=data[:,:48]
X=np.where(X>0 , 1, 0)
print(X)

y=data[:,-1].astype('int')
y

 四、模型拟合、预测与精度

单次训练

from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3)
clf=BernoulliNavieBayes()
clf.train(X_train,y_train)
from sklearn.metrics import accuracy_score
y_pred=clf.predict(X_test)
print(y_pred)
accuracy=accuracy_score(y_test,y_pred)
print(accuracy)

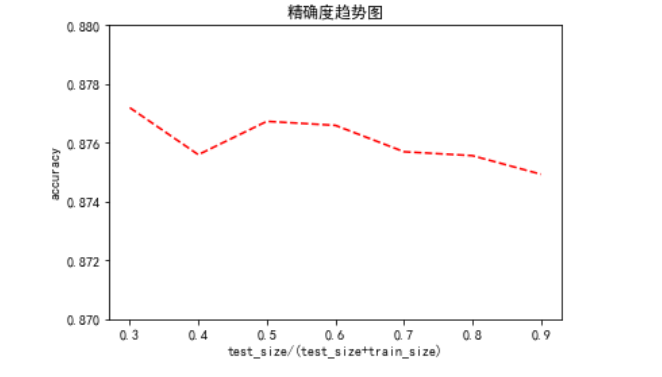
多次训练，精确度没有太多的改变，说明朴素贝叶斯分类器只要很少的样本就能学习到大部分的特征

def test(X,y,test_size,N):
    acc=np.empty(N)
    for i in range(N):
        X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=test_size)
        clf=BernoulliNavieBayes()
        clf.train(X_train,y_train)
        y_pred=clf.predict(X_test)
        acc[i]=accuracy_score(y_test,y_pred)
    return np.mean(acc)

sizes=np.arange(0.3,1,0.1)
print(sizes)
acc=[test(X,y,test_size,100) for test_size in sizes]
print(acc)

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.plot(sizes,acc,linestyle='--',color='red')
plt.ylim([0.87,0.88])
plt.xlabel('test_size/(test_size+trsin_size)')
plt.ylabel('accuracy')
plt.title('精确度趋势图')
plt.show()