题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=3117
求fibonacci数列第n项,如果位数超过八位就求它的前四位和后四位,在此我们知道求后四位是非常简单的,只需要快速幂取模就可以,但是取前四位就需要经过一些操作,证明过程如下。最后为了防止后四位中前面是0,对printf函数参数进行修改。
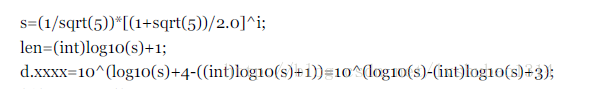
代码如下:
1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef unsigned int ui; 4 typedef long long ll; 5 typedef unsigned long long ull; 6 #define pf printf 7 #define mem(a,b) memset(a,b,sizeof(a)) 8 #define prime1 1e9+7 9 #define prime2 1e9+9 10 #define pi 3.14159265 11 #define lson l,mid,rt<<1 12 #define rson mid+1,r,rt<<1|1 13 #define scand(x) scanf("%llf",&x) 14 #define f(i,a,b) for(int i=a;i<=b;i++) 15 #define scan(a) scanf("%d",&a) 16 #define mp(a,b) make_pair((a),(b)) 17 #define P pair<int,int> 18 #define dbg(args) cout<<#args<<":"<<args<<endl; 19 #define inf 0x7ffffff 20 inline int read(){ 21 int ans=0,w=1; 22 char ch=getchar(); 23 while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();} 24 while(isdigit(ch))ans=(ans<<3)+(ans<<1)+ch-'0',ch=getchar(); 25 return ans*w; 26 } 27 int n,m,t; 28 const int maxn=1e5+10; 29 const ll mod=10000; 30 struct matrix{ 31 ll a[3][3]; 32 matrix operator * (const matrix &x) const 33 { 34 matrix c; 35 f(i,1,2) 36 f(j,1,2) 37 f(k,1,2) 38 { 39 c.a[i][j]=(c.a[i][j]+a[i][k]*x.a[k][j])%mod; 40 } 41 42 return c; 43 } 44 matrix(){ 45 a[1][1]=a[1][2]=a[2][1]=a[2][2]=0; 46 } 47 }; 48 matrix pow(matrix A,int k) 49 { 50 matrix ans; 51 ans.a[1][1]=ans.a[2][2]=1; 52 ans.a[1][2]=ans.a[2][1]=0; 53 while(k) 54 { 55 if(k&1)ans=ans*A; 56 k>>=1; 57 A=A*A; 58 } 59 return ans; 60 } 61 ll a[100]; 62 int main() 63 { 64 //freopen("input.txt","r",stdin); 65 //freopen("output.txt","w",stdout); 66 std::ios::sync_with_stdio(false); 67 matrix A; 68 A.a[1][1]=A.a[1][2]=A.a[2][1]=1;A.a[2][2]=0; 69 a[0]=0;a[1]=1; 70 int pivot=0; 71 f(i,2,100) 72 { 73 a[i]=a[i-1]+a[i-2]; 74 if(a[i]>=100000000) 75 { 76 pivot=i-1;//最后一个八位数 77 break; 78 } 79 } 80 while(~scanf("%d",&n)) 81 { 82 if(n<=pivot) 83 { 84 pf("%d ",a[n]); 85 continue; 86 } 87 else 88 { 89 matrix tmp=pow(A,n-1); 90 ll last=tmp.a[1][1]; 91 double lgs=log10(1.0/sqrt(5))+(double)n*log10((1.0+sqrt(5))/2.0); 92 int d=(int)(pow(10,lgs-(int)lgs+3));//计算前四位 93 pf("%d...%04lld ",d,last) ;//后四位开头如果是0的话就需要补全 94 } 95 } 96 }