「AGC 004C」AND Grid
Tag:「水题无 tag」
连通? 典!
第一张图初始一个 \(\text E\) 形, 所有奇数行涂黑; 第二张图初始一个 \(\exist\) 形, 所有偶数行涂黑. 对于原图的黑格, 在两张图上都涂黑就好啦.
「AGC 004D」Teleporter
Tag:「水题无 tag」
给出的传送门构成的是内向基环树, \(1\) 在环上. 最终答案一定也是一棵内向基环树. 不过, 如果一个点走 \(k\) 步到 \(1\), 它走一步, 再走 \(k\) 步还是到 \(1\), 即环一定是 \(1\) 的自环, 并且树高不超过 \(k\). 啊, 这个树上贪心一下就好了, \(\mathcal O(n)\).
「AGC 004E」Salvage Robots
Tag:「A.DP-杂项」
我做 ... 我 WA 过, 哭哭. 又 WA 了两发, 哭哭.
初步转化是让出口移动, 设出口在四个方向移动的最远距离为 \(u,d,l,r\), 出口坐标为 \((x,y)\), 我们就能刻画当前哪些机器人挂了, 哪些机器人救了. 直接大力 \(f(u,d,l,r)\) DP 即可, 复杂度 \(\mathcal O((nm)^2)\).
「AGC 004F」Namori ^
Tags:「B.贪心」「C.性质/结论」「C.思维」
第三次见面, 又不会了?! 还有上面这种 tag 组合实在是太恐怖了.
树是平凡的, 我们来看看基环树.
对于偶环基环树, 可以发现树上二染色的不会失效. 先去掉一条环边变成树, 此时结论是: 设 \(s_u\) 表示 \(u\) 子树内白点数量减黑点数量, 那么树的答案为 \(\sum_u|s_u|\), 有解当且仅当 \(s_{\text{root}}=0\). 此后, 再加入这条边, 研究这条边带来的传递次数 \(x\), 答案形如 \(\sum_{u\text{ is in circle}}|s_u-x|+\sum_{u\text{ isn't in circle}}|s_u|+x\), 直接取最优的 \(x\) 即可.
对于奇环基环树, 非树边连接了同色点, 相当于能让这对同色点同时反色. 那么 \(s_{\text{root}}\) 为偶数 (\(n\) 为偶数) 就有解, 反色次数可以直接算出来.
总共就一个 \(\mathcal O(n)\), 偶环那里可以 std::nth_element.
「AGC 005C」Tree Restoring
Tag:「水题无 tag」
找到直径长度 \(d\), 保证直径能够连出来, 用剩的点的最远距离应当大于 \(\lceil\frac{d+1}2\rceil\). \(\mathcal O(n)\) 判一判就好.
「AGC 005D」~K Perm Counting ^
Tag:「A.数学-二项式反演」
有一个很形象的转化:
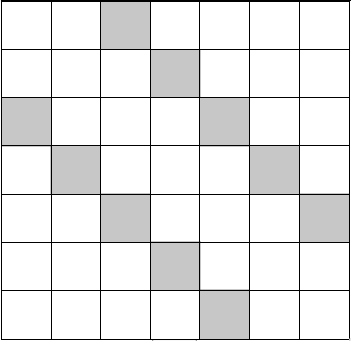
\((i,p_i)\) 描述了网格图中的一个坐标, (图中 \(n=7,k=2\)) 我们的计数目标即在白格子里放 \(n\) 个互不能攻击的车的方案数.
容斥成 "至少放 \(i\) 个阴影", 阴影间的攻击关系是若干条互不干扰的链, 链内的独立集可以直接组合数出来, 外层背包 DP 求出容斥的目标, 然后容斥一下得到答案. 复杂度 \(\mathcal O(n^2)\). 可以多项式做到 \(\mathcal O(n\log n)\).
「AGC 005E」Sugigma: The Showdown *
Tags:「B.贪心」「C.性质/结论」「C.思维」
没有发觉一个显然的结论, 导致根本没法想 qwq.
设先手在红树, 后手在蓝树. 如果先手已经到达了一条红边 \((u,v)\), 使得 \(d_{\text{blue}}(u,v)>2\), 那么先手在这条边上左右横跳就可以让后手自闭了.
因此, 如果有解, 先手不可能走到这样的红边. 也就是说, 认为对于任何红边 \((u,v)\), 都有 \(d_{\text{blue}}(u,v)\le2\). 再注意到, 这样的红边不可能让先手安全地 "跨过" 后手所在位置. 就算 \(d_{\text{blue}}(u,v)=2\), 也顶多从后手所在点的左侧跳到右侧, 然后被后手抓住. 这样并没有站在原地优秀.
更具体化地说, 在蓝树上, 以后手起点为根, 当后手操作最优, 先手只能在后手所在子树内活动. 那么后手的操作就明了了: 一路朝着先手撵过去. 设先后手起点分别为 \(x,y\), 那么先手能走到点 \(u\) 当且仅当 \(d_{\text{red}}(x,u)<d_{\text{blue}}(y,v)\). 结合已有结论, 如果能走到 \(d_{\text{blue}}(u,v)>2\) 的红边, 无解; 否则答案就是能走到的最大的 \(d_{\text{blue}}(y,v)\) 的两倍. 复杂度 \(\mathcal O(n)\).
「AGC 005F」Many Easy Problems
Tags:「A.数学-多项式」「B.Tricks」
很烦呐, 因为不相信 AGC 会拿多项式压轴, 一个小时多才过.
题目所求 "最小连通块" 实际上就是点集的虚树大小. 而关于虚树, 我们有一个经典结论: 设点集 \(S\) 按任意 DFN 排序为 \(\{s_0,s_1,\cdots,s_{k-1}\}\), 则虚树大小为 \(\frac{1}{2}\sum_{i=0}^{k-1}d(s_i,s_{(i+1)\bmod k})+1\).
不过, 这个计算方法仍然以来整个点集, 但我们可以拆开和式, 将贡献转化为 "\(d(u,v)\) 对 \(|S|=k\)" 的贡献. 假设 \(u,v\) DFN 的跨度 (覆盖区间长度, 包含左右端点) 为 \(l\), 则满足 \(|S|=k>1\), \(u,v\in S\) 并且 \(u,v\) DFN 相邻的集合 \(S\) 的数量为 \(\binom{n-l}{k-2}+\binom{l-2}{k-2}\). 注意到如果我们将 \((u,v)\) 按 \(l\) 归类, 求出每类中 \(d(u,v)\) 之和, 就可以差卷积求出答案.
最后的问题变为对于每个 \(l\) 和跨度为 \(l\) 的所有点对 \((u,v)\), 求出 \(d(u,v)\) 之和. 这个距离自然又可以拆成 \(\text{dep}(u)+\text{dep}(v)-2\text{dep}(\text{lca}(u,v))\), 前面两项可以差分 (设 \(u\) 的 DFN 为 \(t\), 则 \(\text{dep}(u)\) 从 \(l=1\) 起贡献两次, 从 \(l=t+1\) 起少贡献一次, 从 \(l=n-t+2\) 起少贡献一次); 后面这个可以先展开成 \(2\sum_{w}[u,v\in\text{subtree}(w)]\), 设 \(w\) 的子树大小为 \(s_w\), 则当 \(l=s_w\) 时 \(-2\), \(l=s_w-1\) 时 \(-2\times2\), ..., 也就是一个二阶差分.
总之, 一次 DFS 挂上差分, 然后算两个差卷积就能求出答案. 复杂度 \(\mathcal O(n\log n)\).
「AGC 006C」Rabbit Exercise
Tags:「B.倍增」「C.性质/结论」
我算是知道 NOIP 2021 C 的原题是什么了.
设 \(f_i\) 表示 \(i\) 号兔子当前的期望位置, 若 \(i\) 需要跳, 跳完后 \(f_i'=f_{i-1}+f_{i+1}-f_i\), 考虑差分 \(d_i=f_i-f_{i-1}\), 就有 \(\{d_i',d_{i+1}'\}=\{d_{i+1},d_i\}\). 倍增这个置换就能求出最终的差分, 也就得到最后的 \(f\). 复杂度 \(\mathcal O(n\log k)\).
「AGC 006D」Median Pyramid Hard
Tags:「A.分治-二分答案」「C.性质/结论」
一遍猜对, 乐.
中位数? 第一个想法当然是二分答案, 紧接着发现难点在于模拟一个 01 序列递推的最终结果.
注意到, 如果 \(a_{i,j}=a_{i,j+1}=t\), 在不考虑撞到边界的情况下, \(t\) 这个值可以左右扩散. 当然, 如果 \(j=n\) (中间位置), 这个 \(t\) 就一定能一路扩散到 \(a_{1,n}\) 处, 得到答案. 当然, 如果一个 \(0\) 的扩散和 \(1\) 的扩散挨在一起, 他们就不能再侵犯对方的领地了.
所以, 我们只关心是 \(0\) 先占领 \(n\) 位置还是 \(1\) 先占领 \(n\) 位置. 直接找到 \(n\) 左右侧第一对 \(a_{i,j}=a_{i,j+1}\), 讨论这两对数的存在性和值, 就能单次 \(\mathcal O(n)\) 判断答案是否不小于某值. 结合外层二分, 复杂度 \(\mathcal O(n\log n)\).
「AGC 006E」Rotate 3x3 *
Tag:「C.性质/结论」
好吧, 这就是 Ad-hoc Grandmaster Contest.
判掉过于离谱的无解后, 可以将原序列转化成一个带正负号的排列. 每次操作选取相邻三个数翻转并取相反数, 需要判断给定排列是否能操作为 \(1,2,\dots,n\).
奇偶是隔离的, 我们需要考虑顺序和正负两个要素, 而前一个要素让我们想到逆序对. 进一步发现, 奇序列的逆序对 \(-1\) 可以带走偶序列任意奇数个负号; 偶序列的逆序对 \(-1\) 可以带走奇序列任意奇数个负号. 那有解条件显然就是: 奇序列逆序对奇偶性等于偶序列负号奇偶性, 偶序列逆序对奇偶性等于奇序列负号奇偶性. 逆序对奇偶性为排列长度减去置换环数量, 可以 \(\mathcal O(n)\) 算. 那么本题就 \(\mathcal O(n)\) 结束了.
「AGC 006F」Blackout *
Tags:「A.构造」「C.性质/结论」「C.思维」
基本的题意转化: 给定一个有向图 \(G=(V,E)\), 若 \(\lang x,y\rang,\lang y,z\rang\in E\), 则可令 \(E\gets E\cup\{\lang z,x\rang\}\). 我们需要求出最终的 \(|E|\).
注意 "选出 \(\lang x,y\rang,\lang y,z\rang\)" 的条件给我们一个暗示: 一条链上连续三个点的 "地位" 是不同的, 进而考虑三染色 (有点牵强啊). 设 \(y\) 的颜色为 \(c\), 则经过 \(\lang y,z\rang\) 时 \(c\gets(c+1)\bmod 3\), 反向经过 \(\lang x,y\rang\) 时 \(c\gets(c-1)\bmod 3\).
这就带来了很多需要讨论的情况. 对于一个弱连通块:
若能够三染色, 并且只用到不超过两种颜色, 显然无法加边, 贡献就是连通块原有边数.
否则若能三染色, 设三色点集大小为 \(s_0,s_1,s_2\), 结论上, 最终贡献为 \(s_0s_1+s_1s_2+s_2s_0\). 归纳证明, 我们需要说明对于任意 \(u,v\), \(\lang u,v\rang\in E\Leftrightarrow c_v=(c_u+1)\bmod 3\). 设 \(G=(V,E)\) 是弱连通的, 且能够三染色, 则令 \(E\) 成为最终的 \(E\). 根据染色规则, 所有新加的边不会破坏 \(G\) 能三染色的性质. 这时, 向点集加入一个点 \(u\) 并加入一些关于 \(u\) 的边, 不妨设存在一个 \(c_p=0\) 的 \(p\), 使得 \(\lang p,u\rang\in E\), 那么 \(c_u\) 被确定为 \(1\). 此时, 对于任意 \(c_q=2\) 的 \(q\), 根据归纳假设, 有 \(\lang q,p\rang,\lang p,u\rang\in E\), 因此 \(\lang u,q\rang\in E\). 对于任意 \(c_r=0\) 的 \(r\), 根据已有结论, 存在一个 \(c_q=2\), 使得 \(\lang u,q\rang,\lang q,r\rang\in E\), 因此 \(\lang r,q\rang\in E\). 不可能存在其他任何边, 不然必定破坏三染色性质.
再否则, 即图无法三染色. 设弱连通块的大小为 \(s\), 结论上, 最终贡献为 \(s^2\). 我们可以先删掉足够的边使得图弱连通且能三染色, 连出如上一种情况的所有边. 接着加入一条矛盾边, 并说明此时足以构造出完全图. 证明类似上一种情况.
于是就 \(\mathcal O(n+m)\) 完成了.