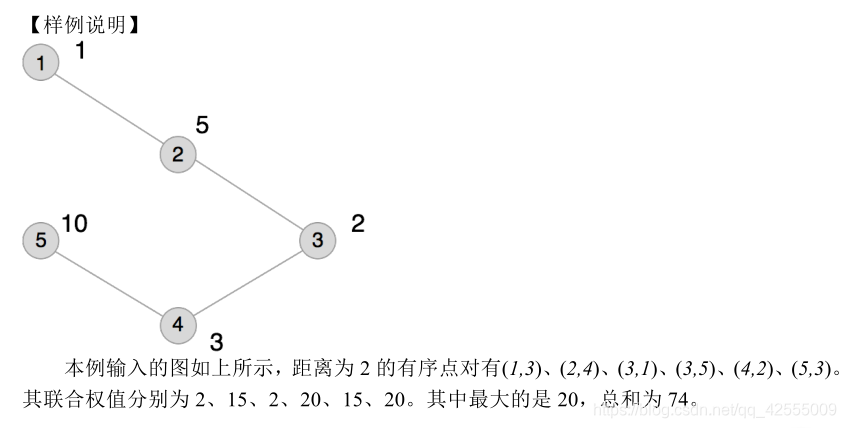
描述
无向连通图G 有n 个点,n - 1 条边。点从1 到n 依次编号,编号为 i 的点的权值为W i ,每条边的长度均为1 。图上两点( u , v ) 的距离定义为u 点到v 点的最短距离。对于图G 上的点对( u, v) ,若它们的距离为2 ,则它们之间会产生Wu×Wv 的联合权值。
请问图G 上所有可产生联合权值的有序点对中,联合权值最大的是多少?所有联合权值之和是多少?
输入
第一行包含1 个整数n 。
接下来n - 1 行,每行包含 2 个用空格隔开的正整数u 、v ,表示编号为 u 和编号为v 的点之间有边相连。
最后1 行,包含 n 个正整数,每两个正整数之间用一个空格隔开,其中第 i 个整数表示图G 上编号为i 的点的权值为W i
输出
输出共1 行,包含2 个整数,之间用一个空格隔开,依次为图G 上联合权值的最大值和所有联合权值之和。由于所有联合权值之和可能很大,输出它时要对10007 取余。
样例输入
5
1 2
2 3
3 4
4 5
1 5 2 3 10
样例输出
20 74
提示
对于30% 的数据,1 < n≤ 100 ;
对于60% 的数据,1 < n≤ 2000;
对于100%的数据,1 < n≤ 200 , 000 ,0 < wi≤ 10, 000 。
看到这道题的第一眼:我靠,这是点分治?
然后第二眼:我靠,这不是傻逼题吗?
考虑到每次是计算距离为2的点,也就是说一个点的父亲和儿子计算一次
我们可以直接dfs,对于每个点维护和他相邻的点的权值和和权值最大值
每搜一个儿子,并用儿子权值乘已有的权值和,并看一下是否能更新最大值,
然后用儿子更新自己的权值和以及最大值
考虑到题目要求的是求所有有序点对的权值和,但这样其实是只把每两个点计算了一次,所以最后权值和要乘2
由于乘起来可能要炸long long
所以要么一直给权值和取膜,要么开long long
#include<bits/stdc++.h>
using namespace std;
inline int read(){
char ch=getchar();
int res=0;
while(!isdigit(ch))ch=getchar();
while(isdigit(ch))res=(res<<3)+(res<<1)+(ch^48),ch=getchar();
return res;
}
const int mod=10007;
const int N=200005;
int a[N],adj[N],n,nxt[N<<1],to[N<<1],maxn[N],cnt,most,ans,tot[N];//most:全局最大值,maxn:每个点的最大值,tot:每个点的权值和
inline void addedge(int u,int v){
nxt[++cnt]=adj[u],adj[u]=cnt,to[cnt]=v;
}
inline void dfs(int u,int fa){
tot[u]=a[fa],maxn[u]=a[fa];
for(int e=adj[u];e;e=nxt[e]){
int v=to[e];
if(v==fa)continue;
if(maxn[u]*a[v]>most)most=maxn[u]*a[v];//更新最大值
ans+=tot[u]*a[v],ans%=mod,tot[u]+=a[v],tot[u]%=mod;//计算权值和并更新权值和
if(a[v]>maxn[u])maxn[u]=a[v];//更新最大值
dfs(v,u);
}
}
signed main(){
n=read();
for(int i=1;i<n;++i){
int u=read(),v=read();
addedge(u,v),addedge(v,u);
}
for(int i=1;i<=n;++i){
a[i]=read();
}
dfs(1,0);
ans=ans*2%mod;//答案要乘2
cout<<most<<" "<<ans%mod;
}