我的模板1.0

0. 头文件

#include<bits/stdc++.h>
using namespace std;
#define fi first
#define se second
#define U unsigned
#define P std::pair<int,int>
#define LL long long
#define pb push_back
#define MP std::make_pair
#define V std::vector<int>
#define all(x) x.begin(),x.end()
#define CLR(i,a) memset(i,a,sizeof(i))
#define FOR(i,a,b) for(int i = a;i <= b;++i)
#define ROF(i,a,b) for(int i = a;i >= b;--i)
#define DEBUG(x) std::cerr << #x << '=' << x << std::endl
#define INF 0x3f3f3f3f
#define lowbit(x) ((x)&-(x))
#define MOD 1000000007
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
const int N=1e5+7;

1. 琐碎操作

1.1 结构体

struct _node{
    int id,a,b;
    bool operator < (const _node k) const{
        if(a==k.a&&b==k.b) return id>k.id;   //相等的话优先把当前放后面
        else return a==k.a?b>k.b:a<k.a;  //题目做得越少越塞前面 
    }
    _node(int id,int a,int b):id(id),a(a),b(b){}
};

1.2 STL

1.2.1 set

性质：set用二叉搜索树实现，集合中的每个元素只出现一次，并且是排好序的。

访问元素的时间复杂度是O(logn)，非常高效。

int main(){
    int n,m;scanf("%d%d",&n,&m);
    FOR(i,1,m){
        int x,y;scanf("%d%d",&x,&y);
        if(x==1){
            a[1]++,b[1]+=y;
            if(!s.empty()){
                set<_node>::iterator it=s.lower_bound(_node(1,a[1],b[1]));
                if(s.begin()!=it) s.erase(s.begin(),it); //把前面都干掉 
            }
        }else{
            if(s.find(_node(x,a[x],b[x]))==s.end()){ //查找
                a[x]++,b[x]+=y;
                if(a[x]>a[1]||(a[x]==a[1]&&b[x]<b[1]))
                    s.insert(_node(x,a[x],b[x]));
            }else{
                s.erase(_node(x,a[x],b[x])); // 删除
                a[x]++,b[x]+=y;
                s.insert(_node(x,a[x],b[x])); //插入
            }
        }
        printf("%d
",s.size()+1);
    }
}

1.2.2 vector

去重

sort(all(x)),sort(all(s));
vector<double>::iterator last=unique(all(x));
x.erase(last,x.end());

lower_bound

int l=lower_bound(all(x),s[i].l)-x.begin()+1;
int r=lower_bound(all(x),s[i].r)-x.begin()+1;

1.3 python

t=int(input())
for i in range(t):
    x,y=map(int,input().split())
    c=list(map(int,input().split()))
    
    path1=abs(x)*c[0 if x>=0 else 3]+abs(y-x)*c[1 if y-x>=0 else 4]
    path2=abs(y)*c[0 if y>=0 else 3]+abs(x-y)*c[5 if x-y>=0 else 2]
    path3=abs(y)*c[1 if y>=0 else 4]+abs(x)*c[5 if x>=0 else 2]
    
    print(min(path1,path2,path3))

国王的游戏（贪心）

N=int(input())
s=input().split()
S=int(s[0])
T=int(s[1])
a=[]#一个列表
for i in range(1,N+1):
    k=input().split()
    a.append((int(k[0]),int(k[1])))
a.sort(key=lambda x:x[0]*x[1])
ans=0
for i in range(0,N):
    if(S//(a[i])[1]>ans):
        ans=S//(a[i])[1]
    S*=(a[i])[0]
print(ans)

for _ in range(int(input())):
    a,b=map(int,input().split())
    print(a^b)

读取到end of file：

if __name__ == '__main__':
    while True:
        try:
            # do stuffs of the problem
        except EOFError:   #end of file退出
            break

进制转换：

十->2

n=int(input())
print(bin(n))

2->十

n=input()
print(int(n,2))

1.4 二分查找

int binary_search(int n,int k){
    int low=1,high=n;
    int mid;
    while(low<=high){
        mid=(high+low)>>1;
        if(a[mid]>k)high=mid-1;
        else if(a[mid]==k){
            if(mid!=1){
                while(a[mid]==k){
                    mid--;
                }
                return mid+1;
            }
            else return mid;
        }
        else low=mid+1; 
    }
    return -1;
}

1.5 尺取法

连续+暴力枚举

#include<iostream>
#include<stdio.h>
#include<set>
#include<cstdio>
#include<string.h>
#include<cstdlib>  
#include<stack>  
#include<queue>  
#include<algorithm>  
#include<cstring>  
#include<string>  
#include<cmath>  
#include<vector>  
#include<bitset>  
#include<list>  
#include<sstream>   
#include<map>
#include<functional> 
using namespace std;
const int N=1e5+5;
const int inf=1e9+7;
int a[N];
typedef unsigned long long ull;
int main(){
    ull s;
    int t;
    scanf("%d",&t);
    while(t--){
        int n;
        scanf("%d%llu",&n,&s);
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
        }
        deque<int>q;
        q.clear();
        ull sum=0;
        int i=1;
        int len=0,ans=inf;
        while(1){
            while(i<=n&&sum<s){
                sum+=a[i];
                q.push_back(a[i++]);
                len++;
            }
            if(sum<s) break;
            ans=min(ans,len);
            len--;
            sum-=q.front();
            q.pop_front();
        }
        if(ans==inf) printf("0
");
        else printf("%d
",ans);
    }
}

2. 动态规划

2.1 背包DP

#include<bits/stdc++.h>
using namespace std;
const int maxn=10000;
int dp[1003];//前：第几种物品 后：所装多少 
int t[maxn+2],c[maxn+2],p[maxn+2];
int m;//全局变量：总时间（背包容量） 
void completepack(int i,int cost,int weight){
    for(int j=0;j<=m;j++){
        if(j>=cost)dp[j]=max(dp[j],dp[j-cost]+weight);
    }
}
void zeroonepack(int i,int cost,int weight){
    for(int j=m;j>=0;j--){
        if(j>=cost)
        dp[j]=max(dp[j],dp[j-cost]+weight);
    }
}
void multiplepack(int i,int cost,int weight,int amount){
    if(cost*amount>=m){
        completepack(i,cost,weight);
        return;
    }
    int k=1;
    while(k<amount){
        zeroonepack(i,k*cost,k*weight);
        amount-=k;
        k*=2;
    }
    zeroonepack(i,amount*cost,amount*weight);
} 
int main(){
    int h1,m1,h2,m2,n;
    scanf("%d:%d %d:%d %d",&h1,&m1,&h2,&m2,&n);
    for(int i=1;i<=n;i++)scanf("%d%d%d",&t[i],&c[i],&p[i]);
    int mx=m2-m1;
    int hx=(h2-h1)*60;
    if(mx<0)hx=(h2-h1-1)*60;
    if(mx<0)mx=60-m1+m2;
    m=hx+mx;
    for(int i=1;i<=n;i++){
        if(p[i]==0)completepack(i,t[i],c[i]);
        else multiplepack(i,t[i],c[i],p[i]);
    }
    printf("%d
",dp[m]);
}

3. 数学

3.1 置换群

求置换的秩k（P^k=1）

#include<iostream>
#include<stdio.h>
#include<set>
#include<cstdio>
#include<string.h>
#include<cstdlib>  
#include<stack>  
#include<queue>  
#include<algorithm>  
#include<cstring>  
#include<string>  
#include<cmath>  
#include<vector>  
#include<bitset>  
#include<list>  
#include<sstream>   
#include<map>
#include<functional> 
using namespace std;
int a[1004],vis[1004];
int gcd(int a,int b){
    return b?gcd(b,a%b):a;
}
int lcm(int a,int b){
    return a/gcd(a,b)*b;
}
int main(){
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;++i){
        scanf("%d",&a[i]);
    }
    int ans=1,tmp;
    for(int i=1;i<=n;++i){
        if(!vis[i]){
            tmp=1;
            vis[i]=1;
            int j=a[i];
            while(!vis[j]){
                vis[j]=1;
                j=a[j];
                ++tmp;
            }
            ans=lcm(ans,tmp); 
        }
    }
    printf("%d
",ans);
}

打表求P^k

#include<iostream>
#include<stdio.h>
#include<set>
#include<cstdio>
#include<string.h>
#include<cstdlib>  
#include<stack>  
#include<queue>  
#include<algorithm>  
#include<cstring>  
#include<string>  
#include<cmath>  
#include<vector>  
#include<bitset>  
#include<list>  
#include<sstream>   
#include<map>
#include<functional> 
using namespace std;
int que[204][204],p[204],key[204];
char ans[204],s[204];
int main(){
    int n;
    while(~scanf("%d",&n)&&n){
        for(int i=1;i<=n;i++){
            scanf("%d",&key[i]);
        }
        memset(que,0,sizeof(que));
        memset(p,0,sizeof(p));
        memset(ans,0,sizeof(ans));
        for(int i=1;i<=n;++i){
            que[0][i]=i;
            p[i]=1;
        }
        for(int i=1;i<=n;++i){
            int k=1;
            while(1){
                que[k][i]=key[que[k-1][i]];
                if(que[k][i]==i) break;
                ++p[i];++k;
            }
        }
        int t;
        while(~scanf("%d",&t)&&t){
            getchar();
            cin.getline(s,sizeof(s));
            int len=strlen(s);
            for(int i=len;i<n;++i) s[i]=' ';
            for(int i=1;i<=n;++i){
                int tt=t%p[i];
                ans[que[tt][i]-1]=s[i-1];
            }
            printf("%s
",ans);
        }
        printf("
");
    }
}

已知P^2的k次幂，求P

#include<cstdio>
const int N=1010;
int a[N],a1[N],a0[N],n,s;
void Getnxt(){
    for(int i=1;i<=n;++i) a0[i]=a1[a1[i]];
    for(int i=1;i<=n;++i) a1[i]=a0[i];
}
bool check(){
    for(int i=1;i<=n;++i) if(a1[i]!=a[i]) return 0;
    return 1;
}
int main(){
    while(~scanf("%d%d",&n,&s)){
        for(int i=1;i<=n;++i) scanf("%d",&a[i]),a1[i]=a[i];
        int len=1;
        for(;;++len){
            Getnxt();
            if(check()) break;
        }
        int u=len-s%len;
        for(int i=1;i<=u;++i) Getnxt();
        for(int i=1;i<=n;++i) printf("%d
",a1[i]); 
    }
}

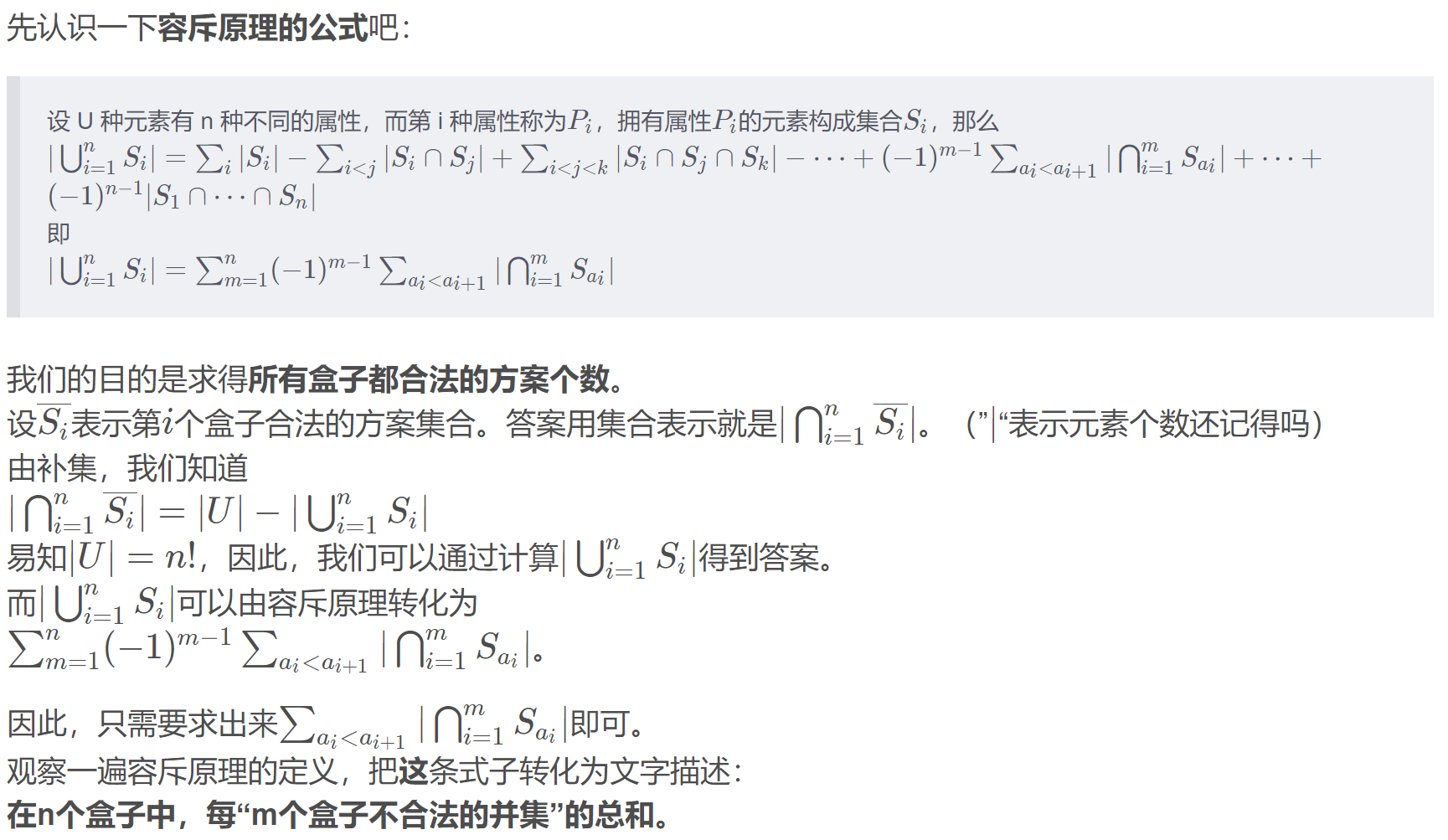
3.2 容斥原理

3.3 数论

3.3.1 欧拉函数

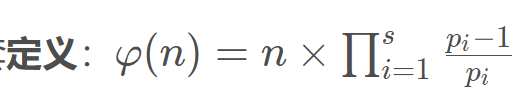
（1）单个求值：定义：对正整数n，欧拉函数是小于或等于n的正整数中与n互质的数的数目

（2）线性筛：

筛质数的线性筛

void init(){
    for(int i=2;i<maxn;i++){
        if(!vis[i]) pri[cnt++]=i;
        for(int j=0;j<cnt&&1ll*i*pri[j]<maxn;j++){
            vis[i*pri[j]]=1;
            //break是因为这个i被pri[j]与之前的某个i筛过了
            //如果i再与其他质数相乘
            //得到的值早就被这个pri[j]筛过
            if(i%pri[j]==0) break;
        }
    }
}

求欧拉函数的线性筛

void get_phi(int n) {
    phi[1]=1;
    for(int i=2;i<=n;i++)
        if(!phi[i])
            for(int j=i;j<=n;j+=i) {
                if(!phi[j]) phi[j]=j;
                phi[j]=phi[j]/i*(i-1);
              }
}

同时求质数和欧拉函数的线性筛：

void init(){
    for(int i=2;i<maxn;i++){
        if(!vis[i]){
            phi[i]=i-1;
            pri[cnt++]=i;
        }
        for(int j=0;j<cnt&&1ll*pri[j]*i<maxn;j++){
            vis[i*pri[j]]=1;
            if(i%pri[j])
                phi[i*pri[j]]=phi[i]*(pri[j]-1);//性质1 
            else {
                phi[i*pri[j]]=phi[i]*pri[j];//性质2 
                break;
            }
        }
    }
}

（3）求前缀和：

（i）线性筛出欧拉函数，老老实实O(n)求前缀和

（ii）杜教筛

（iii）通过莫比乌斯反演来求，要借助莫比乌斯函数，所以已经求出了莫比乌斯函数前缀和时这样做最快。时间复杂度O(n^{frac{2}{3}})

 右边可借由数论分块得出，左边前缀和可借由杜教筛得出。

3.3.2 莫比乌斯函数

 线性筛：

void getMu(){
    mu[1]=1;
    for(int i=2;i<=n;i++){
        if(!vis[i]) p[++tot]=i,mu[i]=-1;
        for(int j=1;j<=tot&&i*p[j]<=n;j++){
            vis[i*p[j]]=1;
            if(i%p[j]==0){
                mu[i*p[j]]=0;
                break;
            }
            mu[i*p[j]]=-mu[i];
        }
    }
}

前缀和筛法：

杜教筛和Min_25筛

杜教筛：

借助数论分块，O(n^{frac{2}{3}})

ll get_large_mu(ll x){
    if(x<n) return sum_mu[x];//预处理（线性筛）计算的
    if(mp_mu.find(x)!=mp_mu.end()) return mp_mu[x];//get_large的时候计算过的
    ll res=1ll;
    for(ll i=2,j;i<=x;i=j+1){//从2开始
        j=x/(x/i);
        res-=get_large_mu(x/i)*(j-(i-1));//数论分块，递归调用
    }
    return mp_mu[x]=res;
}

3.3.3 扩展欧几里得

#include<bits/stdc++.h>
using namespace std;
#define f(x,y,z) for(int x=int(y);x<=int(z);x++)
typedef long long ll;
ll gcd(ll a,ll b,ll &x,ll &y){
    if(b==0){
        x=1,y=0;
        return a;
    }
    ll g=gcd(b,a%b,y,x);//调换x,y
    y-=x*(a/b);//是原处理经过因为调换了xy之后进行的处理
    return g;    
}

int main(){
    ll a,b,c,k;
    scanf("%lld%lld%lld%lld",&a,&b,&c,&k);
    //枚举z的解 
    ll x0,y0;
    ll g=gcd(a,b,x0,y0);
    f(z,0,k/c){
        ll cc=k-c*z;
        //判断是否有整数解：cc是否是a和b的最小公倍数的倍数。
        if(!(cc%g)){
            ll mul=cc/g;
            ll x=mul*x0,y=mul*y0;
            x=(x%(b/g)+(b/g))%(b/g);
            //第一个mod：使得可能为负数的x大于-b/g
            //第二个mod：使得其变为正数
            //第三个mod：使得x为最小正整数（为了让y能大于0） 
            y=(cc-x*a)/b;
            if(x>=0&&y>=0){
                printf("%lld %lld %lld
",x,y,z);
                break;
            }
        } 
    }
}

3.3.4 逆元

求法：

（1）扩展欧几里得（原理：转化为二元一次方程，要求gcd(a,m)=1

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
void ex_gcd(ll a,ll b,ll &x,ll &y){
    if(b==0){
        x=1,y=0;
        return ;
    }
    ex_gcd(b,a%b,y,x);
    y-=a/b*x;
}
ll mod_inverse(ll a,ll m){
    ll x,y;
    ex_gcd(a,m,x,y);
    return (m+x%m)%m;//最小正整数解
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        ll n,b;
        scanf("%lld%lld",&n,&b);
        ll b_inv=mod_inverse(b,9973);
        printf("%d
",n*b_inv%9973);
    }
}

（2）费马小定理求（要求m为质数）

ll inv(ll a){
    return quickpow(a,mod-2);
}

（3）线性求

ll inv(ll a){
    return a==1?1:(long long)(mod-mod/a)*inv(mod%a)%mod;
}

（4）（批量求法）线性求

void Inverse(int m,int inv[],int n){//线性求<=n的数%m意义下的逆元 
    inv[1]=1;
    for(int i=2;i<=n;i++){
        inv[i]=1ll*(m-m/i)*inv[m%i]%m;
    }
}

3.3.5 数论分块

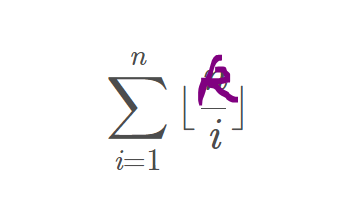
long long ans = 0;
for (long long l = 1, r; l <= n; l = r + 1) {  //此处l意同i,r意同j,下个计算区间的l应为上个区间的r+1
  if (k / l != 0)
    r = min(k / (k / l), n);
  else
    r = n;  // l大于k时
  ans += (k / l) * (r - l + 1);  
}

3.4 组合数学

3.4.1 求组合数

（1）杨辉三角递推公式

（2）乘法逆元

（3）Lucas 定理

void c1(){     // 杨辉三角
    c[0][0]=1;
    for(int i=1;i<maxn;i++){
        c[i][0]=1;c[i][i]=1;
    }
    for(int i=1;i<maxn;i++){
        for(int j=1;j<=i-1;j++){
            c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
        }
    }
}

4. 数据结构

4.1 单调栈

对于数组中每个值，求它右边第一个大于它的值的位置与当前位置之间的值的数目。

从右往左单调栈，维护值为降序的位置。

#include<iostream>
#include<stdio.h>
#include<cstdio>
#include<string.h>
#include<cstdlib>  
#include<stack>    
#include<algorithm>  
#include<cstring>  
#include<string>  
#include<cmath>  
#include<bitset>   
#include<sstream>   
#include<functional>
#define eqfor(i,a,b) for(int i=a;i<=b;++i) 
using namespace std;
typedef long long ll;
stack<ll>s;
ll a[80004];
int main(){
    int n;
    ll ans = 0,x;
    scanf("%d",&n);
    eqfor(i,1,n) scanf("%d",&a[i]);
    for(int i=n;i>=1;--i){
        while(!s.empty()&&a[i]>a[s.top()]) s.pop();
        if(s.empty()) ans += n-i;
        else ans += s.top()-1-i;
        s.push(i);
    }
    printf("%lld
",ans);
}

4.1.2 单调队列

性质：区间最值问题、队列性质

Deque(STL)

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+4;
const int inf=1e9;
int s[N];
int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        int tmp;
        scanf("%d",&tmp);
        s[i]=s[i-1]+tmp;
    }
    deque<int>q;
    q.push_back(0);
    int ans=-inf;
    for(int i=1;i<=n;i++){
        while(q.size()&&q.front()<i-m)
            q.pop_front();
        while(q.size()&&s[q.back()]>=s[i])
            q.pop_back();
        q.push_back(i);
        ans=max(ans,s[i]-s[q.front()]);
    }
    printf("%d
",ans);
}

5. 字符串

5.1 马拉车

求最长回文子串

string preProcess(int len,string s){
    if(len==0) return "^$";
    string ret="^";
    for(int i=0;i<len;++i)
        ret+="#",ret+=s[i];
    ret+="#$";
    return ret;
}

string manacher(int len,string s){
    string T=preProcess(len,s);
    int n=T.length();
    int C=0,R=0;
    for(int i=1;i<n-1;i++){
        int i_mirror=2*C-i;
        if(R>i) P[i]=min(R-i,P[i_mirror]);// 防止超出 R
        else P[i]=0;// 等于 R 的情况
        // 碰到之前讲的三种情况时候，需要利用中心扩展法
        while(T[i+1+P[i]]==T[i-1-P[i]]) P[i]++;
        // 判断是否需要更新 R
        if(i+P[i]>R) C=i,R=i+P[i];
    }
    // 找出 P 的最大值
    int maxLen=0,centerIndex=0;
    for(int i=1;i<n-1;i++)
        if(ed==len&&P[i]>maxLen) maxLen=P[i],centerIndex=i;
    //最开始讲的求原字符串下标
    int st=(centerIndex-maxLen)/2,ed=st+maxLen;
    return s.substr(start,start+maxLen);
}

5.3 AC自动机

#include<bits/stdc++.h>
using namespace std;
const int SZ=500003;
const int N=1000003;
namespace AC{
    int tr[SZ][26],tot;
    int e[SZ],fail[SZ];
    void init(){
        memset(tr,0,sizeof(tr));
        memset(e,0,sizeof(e));
        memset(fail,0,sizeof(fail));
        tot=0;
    }
    void insert(char *s){
        int u=0;
        for(int i=1;s[i];i++){
            if(!tr[u][s[i]-'a']) tr[u][s[i]-'a']=++tot;
            u=tr[u][s[i]-'a'];
        }
        e[u]++;
    }
    queue<int>q;
    void build(){
        for(int i=0;i<26;i++)
            if(tr[0][i]) q.push(tr[0][i]);
        while(q.size()){
            int u=q.front();
            q.pop();
            for(int i=0;i<26;i++){
                if(tr[u][i])
                    fail[tr[u][i]]=tr[fail[u]][i],q.push(tr[u][i]);
                else
                    tr[u][i]=tr[fail[u]][i];
            }
        }
    }
    int query(char *t){
        int u=0,res=0;
        for(int i=1;t[i];i++){
            u=tr[u][t[i]-'a'];
            for(int j=u;j&&e[j]!=-1;j=fail[j])
                res+=e[j],e[j]=-1;
        }
        return res;
    }
}

char s[N];int n,ca;
int main(){
    scanf("%d",&ca);
    while(ca--){
        scanf("%d",&n);
        AC::init();
        for(int i=1;i<=n;i++) scanf("%s",s+1),AC::insert(s);
        scanf("%s",s+1);
        AC::build();
        printf("%d
",AC::query(s));
    }
}

5.4 哈希

void init(){
    base[0]=1;
    for(int i=1;i<N;i++)
        base[i]=base[i-1]*seed; 
}
void makehash(int len){
    for(int i=1;i<=len;i++)
        _hash[i]=_hash[i-1]*seed+(s[i]-'a'+1);
}

取子串的hash：

ull gethash(int i,int l){
    return _hash[i+l-1]-_hash[i-1]*base[l];
}