解决二叉树遍历的画法
对于二叉树的基本概念,一般学生都知道,但对于二叉树的遍历,在实际运用中可以发现很多问题,这里提供一次性彻底解决这个问题的方法。
二叉树的遍历
二叉树的遍历是指不重复地访问二叉树中的所有结点。
由于二叉树是一种非线性结构,因此,对二叉树的遍历要比遍历线性表复杂得多。在遍历二叉树的过程中,当访问到某个结点时,再往下访问可能有两个分支,那么先访问哪一个分支呢?
对于二叉树来说,需要访问根结点、左子树上的所有结点、右子树上的所有结点,在这三者中,究竟先访问哪一个?也就是说,遍历二叉树的方法实际上是要确定访问各结点的顺序,以便不重不漏地访问到二叉树中的所有结点。
在遍历二叉树的过程中,一般先遍历左子树,然后再遍历右子树。在先左后右的原则下,根据访问根结点的次序,二叉树的遍历可以分为三种:前序遍历、中序遍历、后序遍历。这三种说法实际是指对根结点的访问顺序决定的,下面分别介绍这三种遍历的方法。
1.前序遍历(DLR)
所谓前序遍历是指在访问根结点、遍历左子树与遍历右子树这三者中,首先访问根结点,然后遍历左子树,最后遍历右子树;并且,在遍历左、右子树时,仍然先访问根结点,然后遍历左子树,最后遍历右子树。因此,前序遍历二叉树的过程是一个递归的过程。
下面是二叉树前序遍历的简单描述:
若二叉树为空,则结束返回。
否则:
(1)访问根结点;
(2)前序遍历左子树;
(3)前序遍历右子树。
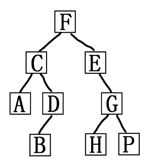
在此特别要注意的是,在遍历左右子树时仍然采用前序遍历的方法。如图所示:二叉树进行前序遍历,则遍历的结果为F,C,A,D,B,E,G,H,P(称为该二叉树的前序序列)。
2.中序遍历(LDR)
所谓中序遍历是指在访问根结点、遍历左子树与遍历右子树这三者中,首先遍历左子树,然后访问根结点,最后遍历右子树;并且,在遍历左、右子树时,仍然先遍历左子树,然后访问根结点,最后遍历右子树。因此,中序遍历二叉树的过程也是一个递归的过程。
下面是二叉树中序遍历的简单描述:
若二叉树为空,则结束返回。
否则:
(1)中序遍历左子树;
(2)访问根结点;
(3)中序遍历左子树。
二叉树进行中序遍历,则遍历结果为A,C,B,D,F,E,H,G,P(称为该二叉树的中序序列)。
在此也要特别注意的是,在遍历左右子树时仍然采用中序遍历的方法。如图所示:
3.后序遍历(LRD) .
所谓后序遍历是指在访问根结点、遍历左子树与遍历右子树这三者中,首先遍历左子树,然后遍历右子树,最后访问根结点,并且,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后访问根结点。因此,后序遍历二叉树的过程也是一个递归的过程。
下面是二叉树后序遍历的简单描述:
若二叉树为空,则结束返回。否则:
(1)后序遍历左子树;
(2)后序遍历右子树;
(3)访问根结点。
在此也要特别注意的是,在遍历左右子树时仍然采用后序遍历的方法。如图所示:
二叉树进行后序遍历,则遍历结果为A,B,D,C,H,P,G,E, F。
配套练习
练习一:
某图遍历顺序如下:
先序遍历:
ABDGCEF
中序遍历:
DGBAECF
请写出该图后续遍历
-------------------------------------------我是分割线 -------------------------------------------
答案:
后序遍历:
GDBEFCA
个人方法:先写出中序投影,再根据中序投影及前序画图,最后写后序,
投影如下图:(非本例题,仅供参考)

从左往右即为中序
还有一个很好的前序解释图: