这题 一开始想就用并查集来做的 但是有个情况处理不了 2个结点在不同的子树上 这样单纯靠深度就无法正确计算了
那么 就只能用Lca了..
话说 lca 写起来 好长啊 很久不写 -.-
其实 这种算法 每个人都有自己的想法 然后 就会形成自己的关于某个算法的模板 所以 去看别人的代码 会觉得大体上能看懂 一些细节就有点不清楚了
这题 反正 折腾了一晚上啊 我擦叻 -.-
主要在查询的时候 一开始的代码是这样的
1 addQedge( mp[x] , mp[y] );
就是for i 0 -> m 然后上面这一段代码
这样其实就是埋下了隐患 =-= 其实很容易举出反例
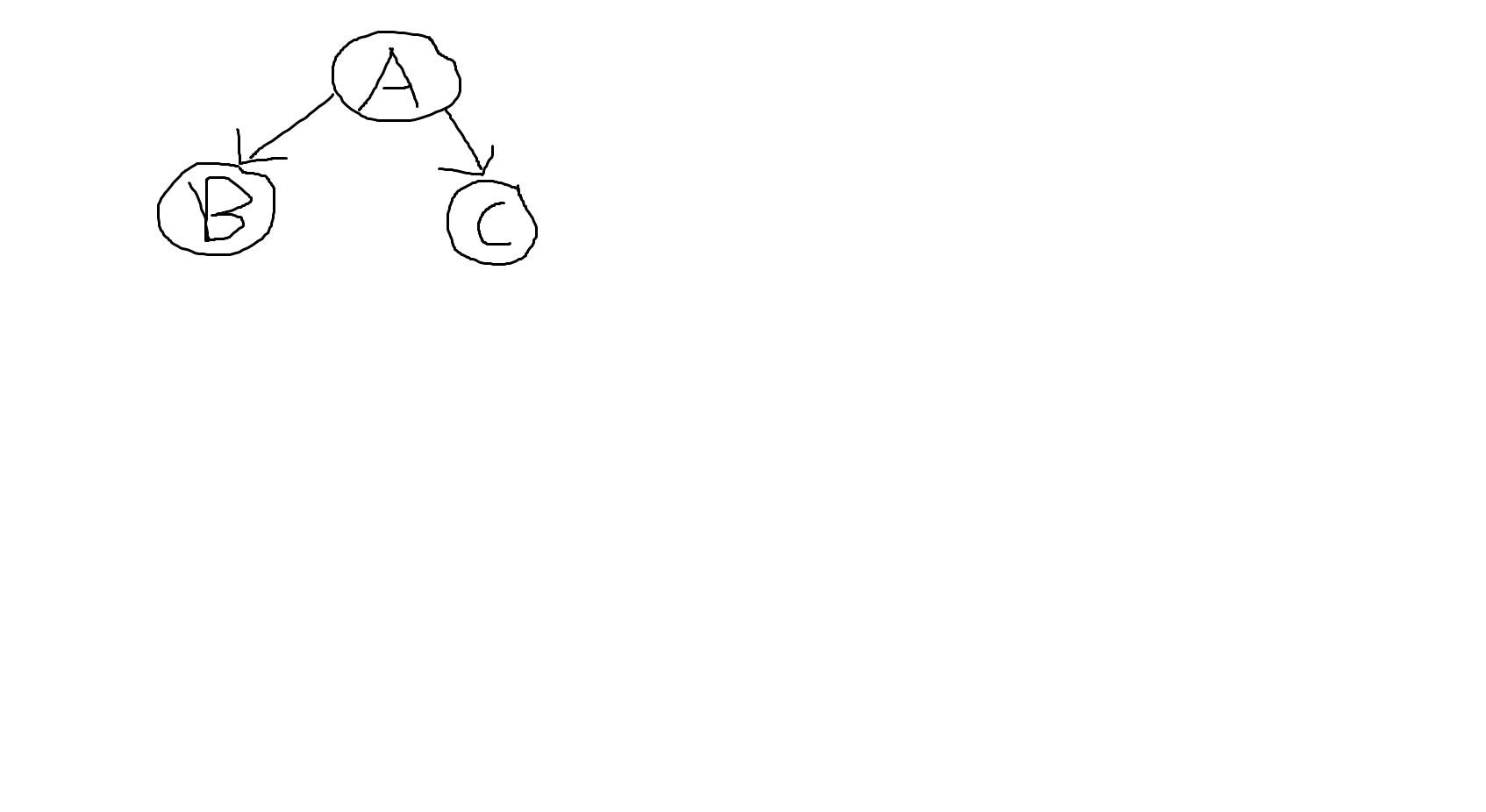
因为 题目明确告诉了我们 确定了根结点 所以其实 建有向图就足够了
然后 如果我的查询是B->C 又很巧的是 我先访问的是A->B这条边 那么当访问到B点的时候 B就会进行询问操作 可是此时C还没有VIS标记过 就无法处理..到了A->C这条边访问到C的时候 可是C并没有查询操作 然后就这样结束了...
所以 修改起来很简单 逆向查询 再添一段
1 addQedge( mp[x] , mp[y] ); 2 addQedge( mp[y] , mp[x] );
OK 现在放上完整代码 感觉蛮好理解的自己的 #17 。

1 #include <iostream> 2 #include <map> 3 #include <cstring> 4 #include <string> 5 using namespace std; 6 7 int num1 , num2; 8 const int size1 = 50; 9 const int size2 = 200010; 10 char x[size1] , y[size1]; 11 map<string,int>mp; 12 struct graph 13 { 14 int from; 15 int to; 16 int lca; 17 int next; 18 }; 19 graph node[size2]; 20 int head[size2]; 21 graph Qnode[size2]; 22 int Qhead[size2]; 23 int dist[size2];; 24 int father[size2]; 25 bool vis[size2]; 26 bool flag[size2]; 27 28 void init( ) 29 { 30 memset( head , -1 , sizeof(head) ); 31 memset( vis , false , sizeof(vis) ); 32 memset( flag , false , sizeof(flag) ); 33 memset( Qhead , -1 , sizeof(Qhead) ); 34 memset( dist , 0 , sizeof(dist) ); 35 } 36 37 void addEdge( int from , int to ) 38 { 39 node[num1].to = to; 40 node[num1].next = head[from]; 41 head[from] = num1 ++; 42 } 43 44 void addQedge( int from , int to ) 45 { 46 Qnode[num2].from = from; 47 Qnode[num2].to = to; 48 Qnode[num2].next = Qhead[from]; 49 Qhead[from] = num2 ++; 50 } 51 52 int find( int x ) 53 { 54 return x == father[x] ? x : father[x] = find( father[x] ); 55 } 56 57 void lca( int u , int var ) 58 { 59 int v; 60 vis[u] = true; 61 dist[u] = var; 62 father[u] = u; 63 for( int i = head[u] ; ~i ; i = node[i].next ) 64 { 65 v = node[i].to; 66 if( !vis[v] ) 67 { 68 lca( v , 1+var ); 69 father[v] = u; 70 } 71 } 72 for( int i = Qhead[u] ; ~i ; i = Qnode[i].next ) 73 { 74 v = Qnode[i].to; 75 if( vis[v] ) 76 { 77 Qnode[i].lca = Qnode[i^1].lca = find(v); 78 } 79 } 80 } 81 82 int main() 83 { 84 cin.sync_with_stdio(false); 85 int t , n , m , root , ans , cnt , id; 86 cin >> t; 87 while( t-- ) 88 { 89 cin >> n >> m; 90 init( ); 91 mp.clear(); 92 num1 = num2 = 0; 93 cnt = 1; 94 while( --n ) 95 { 96 cin >> x >> y; 97 if( mp.find(x)==mp.end() ) 98 mp[x] = cnt ++; 99 if( mp.find(y)==mp.end() ) 100 mp[y] = cnt ++; 101 flag[ mp[x] ] = true; 102 addEdge( mp[y] , mp[x] ); 103 } 104 for( int i = 1 ; i<cnt ; i++ ) 105 { 106 if( !flag[i] ) 107 { 108 root = i; 109 break; 110 } 111 } 112 for( int i = 0 ; i<m ; i++ ) 113 { 114 cin >> x >> y; 115 addQedge( mp[x] , mp[y] ); 116 addQedge( mp[y] , mp[x] ); 117 } 118 lca( root , 0 ); 119 for( int i = 0 ; i<m ; i++ ) 120 { 121 id = i*2; 122 if( Qnode[id].from == Qnode[id].to ) 123 cout << 0 << endl; 124 else if( Qnode[id].lca == Qnode[id].from ) 125 cout << 1 << endl; 126 else if( Qnode[id].lca == Qnode[id].to ) 127 cout << dist[ Qnode[id].from ] - dist[ Qnode[id].to ] << endl; 128 else 129 cout << dist[ Qnode[id].from ] - dist[ Qnode[id].lca ] + 1 << endl; 130 } 131 } 132 return 0; 133 }
today:
世人谓我恋何处
其实只恋何处某
