问题描述
因为前面选手们的帮忙,小蛤智商提升了!他现在在玩一个神奇的游戏:给出了一个n*m的棋盘,其中的格子有的黑,有的白。我们对一个格子进行操作,可以使这个格子与它所处的颜色相同的联通块中的所有格子颜色全部取反。问至少要多少次操作可以使所有格子变白?
输入格式
第一行两个整数n,m代表棋盘尺寸;
接下n行一个字符串描述每一行棋盘情况:W为白B为黑。
输出格式
输出一个整数表示最少的次数。
样例输入

样例输出
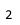
数据范围

题解
把每个格子看成点,考虑对于一个点和另一个点最少需要多少次操作,使得两点在同一同色连通块中。相邻格子之间连一条边,权值为使这两个格子在同一同色连通块中最少需要的操作次数,即,如果两个格子颜色相同,则边的权值为0,否则边的权值为1。那么使得任意两点在同一连通块中的最小操作次数就是这两点之间的最短路径。定义Sx,y表示所有点与格子(x,y)最短路的最大值,那么这就是所有点与格子(x,y)在同一个连通块中的最少操作次数,由于需要变为全白,所以如果最终形成一个黑色的连通块Sx,y需要+1。答案即为所有Sx,y中的最小值。
1 #pragma GCC optimize(2) 2 #pragma GCC optimize(3) 3 #include <cstring> 4 #include <cstdio> 5 const int dx[4]={-1,1,0,0}; 6 const int dy[4]={0,0,-1,1}; 7 const int maxn=5000; 8 struct node{ 9 int u,w,nex; 10 }g[40000]; 11 int n,m,a[75][75],fir[5000],num,ans=1e9; 12 int q[5000],h,t,dis[5000]; 13 bool vis[5000]; 14 char ch[75]; 15 int min(int x,int y) 16 { 17 return x<y?x:y; 18 } 19 void add(int x,int y,int z) 20 { 21 g[++num].u=y; g[num].w=z; g[num].nex=fir[x]; fir[x]=num; 22 return; 23 } 24 void build() 25 { 26 int i,j,k,xx,yy; 27 for (i=1;i<=n;i++) 28 for (j=1;j<=m;j++) 29 for (k=0;k<4;k++) 30 { 31 xx=i+dx[k]; yy=j+dy[k]; 32 if (xx<1 || yy<1 || xx>n || yy>m) continue; 33 add((i-1)*m+j,(xx-1)*m+yy,a[i][j]^a[xx][yy]); 34 add((xx-1)*m+yy,(i-1)*m+j,a[i][j]^a[xx][yy]); 35 } 36 return; 37 } 38 int spfa(int s) 39 { 40 int i,j,k,u,v,step,res=0; 41 memset(dis,127,sizeof(dis)); 42 h=0; t=1; dis[s]=0; q[1]=s; vis[s]=1; 43 while (h!=t) 44 { 45 (++h)%=maxn; u=q[h]; vis[u]=0; 46 for (k=fir[u];k;k=g[k].nex) 47 { 48 v=g[k].u; 49 if (dis[v]>dis[u]+g[k].w) 50 { 51 dis[v]=dis[u]+g[k].w; 52 if (!vis[v]) 53 { 54 vis[v]=1; 55 (++t)%=maxn,q[t]=v; 56 } 57 } 58 } 59 } 60 for (i=1;i<=n;i++) 61 for (j=1;j<=m;j++) 62 { 63 if (dis[(i-1)*m+j]+a[i][j]>res) 64 res=dis[(i-1)*m+j]+a[i][j]; 65 } 66 return res; 67 } 68 int main() 69 { 70 int i,j,k; 71 scanf("%d%d",&n,&m); 72 for (i=1;i<=n;i++) 73 { 74 scanf("%s",ch+1); 75 for (j=1;j<=m;j++) 76 a[i][j]=(ch[j]=='B'); 77 } 78 if (n==1 && m==1) 79 { 80 printf("%d",a[1][1]); 81 return 0; 82 } 83 build(); 84 for (i=1;i<=n*m;i++) 85 ans=min(ans,spfa(i)); 86 printf("%d",ans); 87 return 0; 88 }