降维
机器学习领域中所谓的降维就是指采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数 f : x->y,其中x是原始数据点的表达,目前最多使用向量表达形式。 y是数据点映射后的低维向量表达,通常y的维度小于x的维度(当然提高维度也是可以的)。
降维有什么作用呢?
- 数据在低维下更容易处理、更容易使用;
- 相关特征,特别是重要特征更能在数据中明确的显示出来;如果只有两维或者三维的话,更便于可视化展示;
- 去除数据噪声
- 降低算法开销
PCA
PCA是不考虑样本类别输出的无监督降维技术。
总结一下PCA的算法步骤:
设有m条n维数据。
1)将原始数据按列组成n行m列矩阵X
2)将X的每一行(代表一个属性字段)进行零均值化,即减去这一行的均值
3)求出协方差矩阵
4)求出协方差矩阵的特征值及对应的特征向量
5)将特征向量按对应特征值大小从上到下按行排列成矩阵,取前k行组成矩阵P
6)即为降维到k维后的数据
实例分析(以二维特征举例):
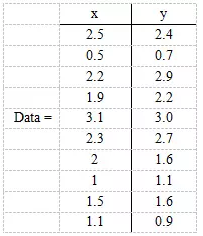
现在假设有一组数据如下:
行代表了样例,列代表特征,这里有10个样例,每个样例两个特征。
第一步,分别求x和y的平均值,然后对于所有的样例,都减去对应的均值。这里x的均值是1.81,y的均值是1.91,得到
第二步,求特征协方差矩阵,如果数据是3维,那么协方差矩阵是
因为这里只有x和y,所以协方差矩阵为
对角线上分别是x和y的方差,非对角线上是协方差。协方差是衡量两个变量同时变化的变化程度。协方差大于0表示x和y若一个增,另一个也增;小于0表示一个增,一个减。如果x和y是统计独立的,那么二者之间的协方差就是0;但是协方差是0,并不能说明x和y是独立的。协方差绝对值越大,两者对彼此的影响越大,反之越小。协方差是没有单位的量,因此,如果同样的两个变量所采用的量纲发生变化,它们的协方差也会产生树枝上的变化。
第三步,求协方差的特征值和特征向量,得到
上面是两个特征值,下面是对应的特征向量,这里的特征向量都归一化为单位向量。
第四步,将特征值按照从大到小的顺序排序,选择其中最大的k个,然后将其对应的k个特征向量分别作为列向量组成特征向量矩阵。
这里特征值只有两个,我们选择其中最大的那个,这里是1.28402771,对应的特征向量是(-0.677873399, -0.735178656)T。
第五步,将样本点投影到选取的特征向量上。
得到的结果是
 * (-0.677873399, -0.735178656)T=
* (-0.677873399, -0.735178656)T= 
这样,就将原始样例的n维特征变成了k维,这k维就是原始特征在k维上的投影。
代码实现:
from sklearn.decomposition import PCA import numpy as np from sklearn.preprocessing import StandardScaler x=np.array([[10001,2,55], [16020,4,11], [12008,6,33], [13131,8,22]]) x_scaler = StandardScaler() x = X
x_scaler.fit_transform(x) pca = PCA(n_components=2) pca.fit(x) Z=pca.transform(x)
LDA
LDA是一种监督学习的降维技术,也就是说它的数据集的每个样本是有类别输出的。这点和PCA不同。LDA的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。什么意思呢? 我们要将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
LDA算法步骤:
1) 计算类内散度矩阵
2) 计算类间散度矩阵
3) 计算矩阵
4)计算的最大的d个特征值和对应的d个特征向量,得到投影矩阵[Math Processing Error]W
5) 对样本集中的每一个样本特征,转化为新的样本
6) 得到输出样本集
部分代码实现:
# -*- coding: utf-8 -*- """ Created on Fri Dec 1 10:49:37 2017 LDA_learning @author: BruceWong """ import pandas as pd import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn import datasets from sklearn.discriminant_analysis import LinearDiscriminantAnalysis import numpy as np def main(): iris = datasets.load_iris() #典型分类数据模型 #这里我们数据统一用pandas处理 data = pd.DataFrame(iris.data, columns=iris.feature_names) data['class'] = iris.target #这里只取两类 # data = data[data['class']!=2] #为了可视化方便,这里取两个属性为例 X = data[data.columns.drop('class')] Y = data['class'] #划分数据集 x_train, x_test, y_train, y_test =train_test_split(X, Y) lda = LinearDiscriminantAnalysis(n_components=2) lda.fit(x_train, y_train) #显示训练结果 print(lda.means_) #中心点 print(lda.score(x_test, y_test)) #score是指分类的正确率 print(lda.scalings_)#score是指分类的正确率 x_2d = lda.transform(X) #现在已经降到二维X_2d=np.dot(X-lda.xbar_,lda.scalings_) #对于二维数据,我们做个可视化 #区域划分 lda.fit(x_2d,Y) h = 0.02 x_min, x_max = x_2d[:, 0].min() - 1, x_2d[:, 0].max() + 1 y_min, y_max = x_2d[:, 1].min() - 1, x_2d[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) Z = lda.predict(np.c_[xx.ravel(), yy.ravel()]) Z = Z.reshape(xx.shape) plt.contourf(xx, yy, Z, cmap=plt.cm.Paired) #做出原来的散点图 class1_x = x_2d[Y==0,0] class1_y = x_2d[Y==0,1] l1 = plt.scatter(class1_x,class1_y,color='b',label=iris.target_names[0]) class1_x = x_2d[Y==1,0] class1_y = x_2d[Y==1,1] l2 = plt.scatter(class1_x,class1_y,color='y',label=iris.target_names[1]) class1_x = x_2d[Y==2,0] class1_y = x_2d[Y==2,1] l3 = plt.scatter(class1_x,class1_y,color='r',label=iris.target_names[2]) plt.legend(handles = [l1, l2, l3], loc = 'best') plt.grid(True) plt.show() if __name__ == '__main__': main()
两者对比
1、相同点
(1)两者的作用是用来降维的
(2)两者都假设符合高斯分布
2、不同点
(1)LDA是有监督的降维方法,PCA是无监督的。
(2)LDA降维最多降到类别数K-1的维数,PCA没有这个限制。
(3)LDA更依赖均值,如果样本信息更依赖方差的话,效果将没有PCA好。
(4)LDA可能会过拟合数据。
参考博客:https://blog.csdn.net/Chenzhi_2016/article/details/79451201




