Tarjan 算法详解

刚学的一个 新算法，终于有时间来整理一下了。

　　想必都对著名的 ‘太监’ 算法早有耳闻了吧。

Tarjan

　　Tarjan 算法是一种求解有向图强连通分量的算法，它能做到线性时间的复杂度。

　　实现是基于DFS爆搜，深度优先搜索一张有向图。！注意！是有向图。然后根据树，堆栈，打标记等种种神奇 扯淡方法来完成拆解一个图的工作。

　　如果要理解Tarjan，我们首先要了解一下，什么叫做强连通。

---

强连通

　　首先，我们将可以相互通达的两个点，称这两个点是强连通的。

　　自然，对于一张图，它的每两个点都强连通，那么这张图就是一张强连通图。

　　而一张有向图中的极大强连通子图就被命名为强连通分量。

  那么，举个栗子吃吧。

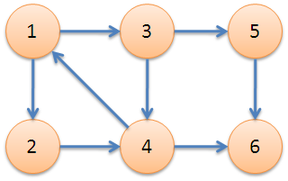            （盗图小丸子光荣上线，come from 百度）

　　对于上面的那张有向图来说，{1,2,3,4}，{5}，{6}分别相互连通，是这张图的三个强连通分量。

---

算法思想简解

　　  Tarjan是在dfs的基础上将每一个强连通分量当做搜索树种的一个子树的遍历方法。

　　那么我们就可以在搜索的时候，将当前的树中没有访问过的节点加入堆栈，然后在回溯的时候判断栈顶到其中的节点是否是一个强连通分量。

　　故而我们在遍历的时候，定义如下变量来记录我们的遍历过程。

　　　　1.dfn[i]=时间戳（节点i被搜索的次序）

　　　　2.low[i]=i或i的子树所能寻找到的栈中的节点序号。

　　所以，当dfn[i]==low[i]时，i或i的子树可以构成一个强连通分量。

---

算法图解（盗图愉悦）

　　　　

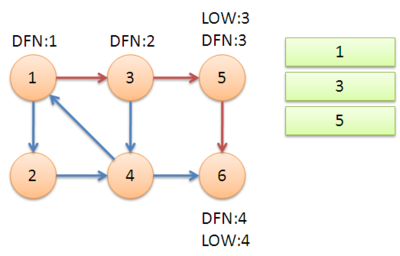
　　在这张图中我们从节点1开始遍历，依次将1， 3，5加入堆栈。当搜索到节点6时，发现没有可以向前走的路，开始回溯。

　　回溯的时候会发现low[5]=dfn[5],low[6]=dfn[6]，那么{5}，{6}分别是两个强连通分量。

　　直到回溯至节点3，拓展出节点4.

　　　　　　

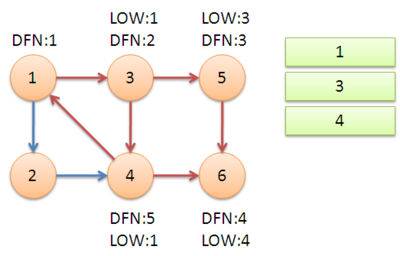
　　结果自然就是拓展到了节点1，发现1在栈中，于是就用1来更新low[4]=low[3]=1;

　　然后回溯节点1，将点2加入堆栈中。

　　　　　　

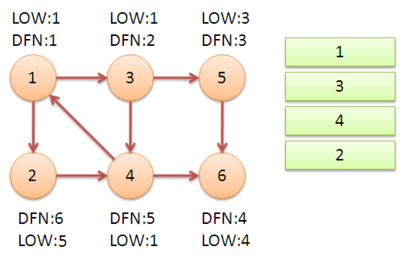
　　然后，Tarjan算法就这么简单的就结束了。

　　很显然，Tarjan算法的复杂度只有O(E+V)啦。线性愉快。

---

算法模板

　　双手奉上我丑陋的代码。

void Tar(int now) {
    dfn[now]=low[now]=++ti;
    sk[++p]=now;
    vis[now]=1;
    for(int i=head[now];i;i=d[i].nxt) {
        int nx=d[i].to;
        if(!dfn[nx]) {
            Tar(nx);
            low[now]=min(low[now],low[nx]);
        }
        else if(vis[nx]) low[now]=min(low[now],dfn[nx]);
    }
    if(low[now]==dfn[now]) {
        while(sk[p+1]!=now) {
            val[now]+=val[sk[p]];
            vis[sk[p]]=0;
            --p;
        }
        val[now]>>=1;
    }
}

希望可以很简洁易懂！！

谢谢。