先来看一下朴素的暴力
dp[i]表示前i个装完的最小花费,再加个前缀和
#include<bits/stdc++.h>
using namespace std;
long long c[50010],sum[50010],dp[50010];
int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
return x*f;
}
int main()
{
int n=read(),l=read();
for(int i=1;i<=n;i++)
{
c[i]=read();
sum[i]=sum[i-1]+c[i];
}
memset(dp,0x3f,sizeof(dp));
dp[0]=0;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=i;j++)
{
long long x=i-j+sum[i]-sum[j-1]-l;
dp[i]=min(dp[i],dp[j-1]+x*x);
}
}
cout<<dp[n];
return 0;
}
n^2^过百万我觉得可以莽一下复杂度是不对的
考虑优化
把转移方程写开
dp[i]=dp[j-1]+(i-j+sum[i]-sum[j-1]-l)2
用k代替j-1再简单移项
dp[i]=dp[k]+(i+sum[i]-k-1-sum[k]-l)2
再设a[i]=i+sum[i],b[k]=k+1+sum[k]+l换掉i和k
得到
dp[i]=dp[k]+(a[i]-b[k])2
dp[i]=dp[k]+a[i]2+b[k]2-2a[i]*b[k]
整理成y=kx+b的形式(y,x只与从哪个转移k的决策有关,k、b只与当前i有关
dp[k]+b[k]2 (y) =2a[i] (k) b[k] (x) -a[i]2+dp[i](b)
因为a[i]2是定值所以求min(dp[i])也就是求min(b)
也就是求直线y=kx+b在知道斜率和直线上一点(x,y)时的最小截距(与y轴)
如果将所有的决策也就是所有的(x,y)在平面直角坐标系上描出来
并从下往上平移一条斜率为k的直线直至一点(x,y)在直线上

可以发现当直线第一次碰到一个点时截距是最小的
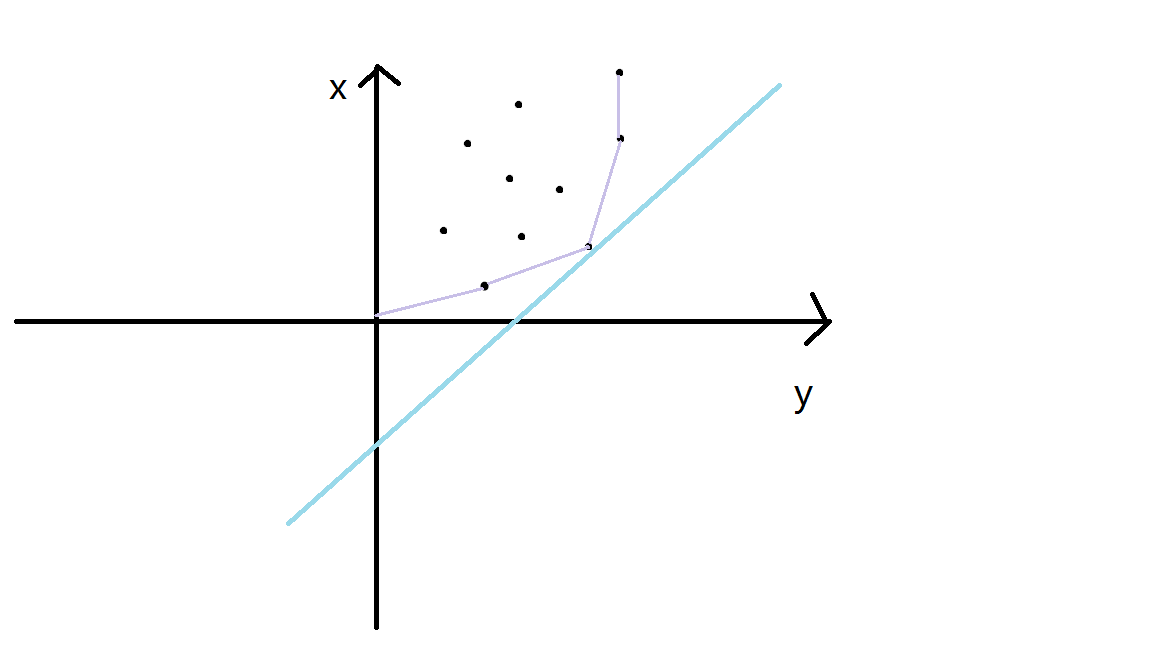
这个第一个碰到的点一定是在凸包上的而且满足这个点与左边的点连线斜率比当前直线斜率小,与右边的点连线斜率比当前斜率大
这是很有用的性质
又因为当前直线的斜率2a[i]=2(sum[i]+i)是递增的
“满足这个点与左边的点连线斜率比当前直线斜率小,与右边的点连线斜率比当前斜率大”的点是可以用单调队列维护的
于是把所有点(决策)用单调队列维护,不在凸包上的点弹出去,又老又弱的弹出去
如何知道一个点不在凸壳上?

加入粉点以后蓝点就不在凸壳上了
也就是当蓝边(队首元素与队内前一个元素的连边)的斜率小于紫边(队首元素与新入队的点的连边)的斜率的时候就要删掉蓝点(队首元素)
#include<bits/stdc++.h>
using namespace std;
long long c[50010],a[50010],line[50010],b[50010],sum[50010],dp[50010];
//qwq像这种每个数都接近int范围,n还很大还要加和的,要开longlong的呀
int read()
{
int x=0,f=1;
char ch=getchar();
while(ch<'0'||ch>'9')
{
if(ch=='-') f=-1;
ch=getchar();
}
while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
return x*f;
}
double slope(int r,int l)//传进来两个点(右边的和左边的)求斜率
//qwq是double不是int别忘了
{
double xl=b[l],yl=dp[l]+b[l]*b[l],xr=b[r],yr=dp[r]+b[r]*b[r];
return (yr-yl)/(xr-xl);
}
int main()
{
int n=read(),l=read();
for(int i=1;i<=n;i++)
{
c[i]=read();
sum[i]=sum[i-1]+c[i];
a[i]=i+sum[i];
b[i]=i+1+sum[i]+l;
}
//因为没有min操作dp初始化为0即可,dp[0]也就等于0
int head=1,tail=1;//初始时队列中有一个横坐标为0的点 ,从该点转移表示当前点单独装
b[0]=l+1; //同上i=0时b的值
for(int i=1;i<=n;i++)//从1开始考虑
{
while(tail>=head+1&&slope(line[head],line[head+1])<=2*a[i]) head++;//比当前直线斜率小肯定比后面的都小
dp[i]=dp[line[head]]+(a[i]-b[line[head]])*(a[i]-b[line[head]]);//状态转移
while(tail>=head+1&&slope(i,line[tail])<slope(line[tail],line[tail-1])) tail--;
line[++tail]=i;//把当前结点加入队列
}
cout<<dp[n];
return 0;
}