题目描述
给定n个各不相同的无序字母对(区分大小写,无序即字母对中的两个字母可以位置颠倒)。请构造一个有n+1个字母的字符串使得每个字母对都在这个字符串中出现。
输入输出格式
输入格式:第一行输入一个正整数n。
以下n行每行两个字母,表示这两个字母需要相邻。
输出格式:输出满足要求的字符串。
如果没有满足要求的字符串,请输出“No Solution”。
如果有多种方案,请输出前面的字母的ASCII编码尽可能小的(字典序最小)的方案
输入输出样例
说明
【数据规模与约定】
不同的无序字母对个数有限,n的规模可以通过计算得到。
题解
首先翻译一下题面吧。
给定n条无向边,试构造一条路径恰好经过每条边1次。
如果可以构造,输出途径的点的编号。
否则输出No Solution。
其实想明白所谓的字母对只是无向边的话,这道题就是很清晰的欧拉路径了。
——以下来自欧拉回路路径求解 - STILLxjy - CSDN博客——
Hierholzer 算法:
另一种计算欧拉路的算法是 Hierholzer 算法。这种算法是基于这样的观察:
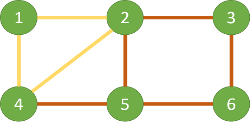
在手动寻找欧拉路的时候,我们从点 4 开始,一笔划到达了点 5,形成路径 4-5-2-3-6-5。此时我们把这条路径去掉,则剩下三条边,2-4-1-2 可以一笔画出。这两条路径在点 2 有交接处(其实点 4 也是一样的)。那么我们可以在一笔画出红色轨迹到达点 2 的时候,一笔画出黄色轨迹,再回到点 2,把剩下的红色轨迹画完。
由于明显的出栈入栈过程,这个算法可以用 DFS 来描述。
如果想看得更仔细一点,下面是从点 4 开始到点 5 结束的 DFS 过程,其中 + 代表入栈,- 代表出栈。
4+ 5+ 2+ 3+ 6+ 5+ 5- 6- 3- 1+ 4+ 2+ 2- 4- 1- 2- 5- 4-
我们把所有出栈的记录连接起来,得到
5-6-3-2-4-1-2-5-4诸位看官可以自己再选一条路径尝试一下。不过需要注意的是,起始点的选择和 Fleury 要求的一样。
这个算法明显要比 Fleury 高效,它不用判断每条边是否是一个桥。
Hierholzer的复杂度是$O(E)$的,所以就套欧拉路径的板子就好啦。
(实在没懂怎么“计算得到”n的规模,好在不用这个条件QAQ
1 /* 2 qwerta 3 P1341 无序字母对 4 Accepted 5 100 6 代码 C++,1.46KB 7 提交时间 2018-09-30 11:11:47 8 耗时/内存 9 28ms, 1052KB 10 */ 11 #include<algorithm> 12 #include<iostream> 13 #include<cstdio> 14 #include<stack> 15 using namespace std; 16 int g[253][253]; 17 int d[253];//度数 18 stack<int>st;//这个是记录栈,不是搜索栈! 19 void dfs(int x)//dfs找点 20 { 21 for(int j='A';j<='z';++j)//这样循环就可以保持字典序最小啦 22 if(g[x][j]) 23 { 24 g[x][j]--; 25 g[j][x]--;//反向边也要删 26 dfs(j);//继续递归 27 } 28 st.push(x);//出栈的时候记录下来 29 return; 30 } 31 int fa[257];//用并查集维护是否有多个联通块 32 int fifa(int x) 33 { 34 if(fa[x]==x)return x; 35 return fa[x]=fifa(fa[x]); 36 } 37 int main() 38 { 39 //freopen("a.in","r",stdin); 40 ios::sync_with_stdio(false); 41 cin.tie(false),cout.tie(false);//关闭同步流(cin伴侣 42 int n; 43 cin>>n; 44 for(int i='A';i<='z';++i)//初始化并查集 45 fa[i]=i; 46 for(int i=1;i<=n;++i) 47 { 48 char x,y; 49 cin>>x>>y; 50 g[x][y]++; 51 g[y][x]++;//临接矩阵存边 52 d[x]++; 53 d[y]++;//度数++ 54 int u=fifa(x),v=fifa(y); 55 if(u!=v)fa[u]=v;//维护并查集 56 } 57 //判定是否有解 58 int num=0; 59 for(int i='A';i<='z';++i) 60 if(d[i]%2==1)num++; 61 if(num!=0&&num!=2){cout<<"No Solution";return 0;} 62 int tag=0; 63 for(int i='A';i<='z';++i) 64 if(d[i]) 65 { 66 if(!tag)tag=i; 67 else if(fifa(tag)!=fifa(i)){cout<<"No Solution";return 0;} 68 } 69 //找是否有奇点 70 int s=-1; 71 for(int i='A';i<='z';++i) 72 if(d[i]%2==1){s=i;break;} 73 if(s==-1)//如果没有奇点就找AscII最小的点 74 for(int i='A';i<='z';++i) 75 if(d[i]){s=i;break;} 76 dfs(s);//递归找点 77 while(!st.empty()) 78 { 79 cout<<(char)st.top(); 80 st.pop(); 81 }//输出 82 return 0; 83 }
皮一下:
