网址:http://codevs.cn/problem/3031/
这是蒟蒻写的第一道字典树……听说出市选题的神犇要出字符串,于是就赶紧滚去学了学(然而高精度算字符串算法?)
简单来说,字典树就是把一坨字符串按照字典序储存起来。然而,直接把字符串排序太浪费空间,而且时间效率也不佳。于是,我们就需要字典树了。
字典树的大致存储方式就是:
假设有5个字符串:a,abc,ab,acb,abd,字典树的存储方式就是把两个字符串相同的前缀合并起来(比如abc和abd有公共的前缀ab,那么就把两个ab合并起来,把剩下的b和c作为ab的两个分支)。
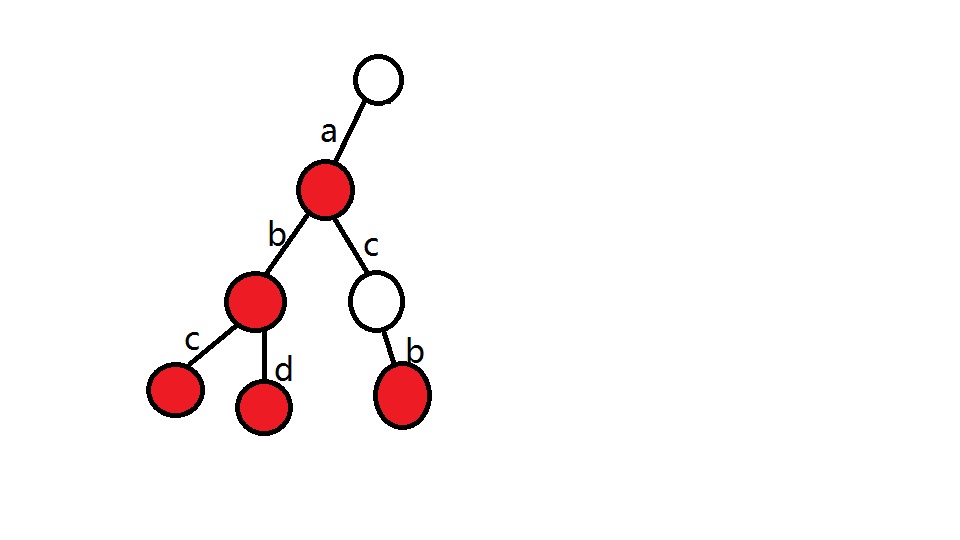
具体可以看图:(其中每条边旁边的字母表示这条边代表的字符,红色的节点代表有字符串在这里结束,从根到红色节点的路径上的字符串起来就是它代表的字符串)
然而,我们知道了字典树,这道题应该怎么做呢?如果只是单纯的排序,用快排就能完成,为什么还要用字典树呢?
我们分析一下题目。题目要求集合中任意数对中最大的xor值,xor的运算规则是相同则0,不同则1,并且不同位之间的运算结果不会相互影响。所以,我们可以发现,如果在高位的值相同的情况下,选择让两个数的这一位取不同的数一定比取相同的数更优(1+2+4+……+2^(n-1)=2^n-1<2^n)。所以我们可以利用字典数的树结构,在树上用两个指针爆搜,如果有不同的路可以走就走不同的路,否则再走相同的路。
于是这道题就完了。。。
代码:

uses math; type tree=record c:array[0..1]of longint; flag:boolean; end; var n,m,i,j,k,p:longint; num:array[0..100]of longint; a:array[0..4000100]of tree; procedure add(dep,now:longint); begin if dep=32 then begin a[now].flag:=true; exit; end; if a[now].c[num[dep]]=0 then begin inc(m); a[now].c[num[dep]]:=m; end; add(dep+1,a[now].c[num[dep]]); end; function dfs(dep,x,y:longint):longint; var ans,i,j:longint; begin if dep=32 then exit(0); ans:=-1; if(a[x].c[0]>0)and(a[y].c[1]>0)then ans:=max(ans,dfs(dep+1,a[x].c[0],a[y].c[1])); if(a[x].c[1]>0)and(a[y].c[0]>0)then ans:=max(ans,dfs(dep+1,a[x].c[1],a[y].c[0])); if(ans>=0)then exit(ans+1<<(31-dep)); if(a[x].c[0]>0)and(a[y].c[0]>0)then ans:=max(ans,dfs(dep+1,a[x].c[0],a[y].c[0])); if(a[x].c[1]>0)and(a[y].c[1]>0)then ans:=max(ans,dfs(dep+1,a[x].c[1],a[y].c[1])); exit(ans); end; begin read(n); m:=1; for i:=1 to n do begin read(k); for j:=1 to 31 do begin num[32-j]:=k and 1; k:=k>>1; end; add(1,1); end; writeln(dfs(1,1,1)); end.
