1.1 定义
设 X1,X2,......Xn相互独立, 都服从标准正态分布N(0,1), 则称随机变量χ2=X12+X22+......+Xn2所服从的分布为自由度为 n 的χ2分布.[1]
卡方分布的 期望E(χ2)=n,方差D(χ2)=2n。
卡方分布:若n个相互独立的随机变量ξ₁、ξ₂、……、ξn ,均服从标准正态分布N(0,1)(也称独立同分布于标准正态分布),则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量,其分布规律称为 分布(chi-squaredistribution)。其中参数n称为自由度(通俗讲,样本中独立或能自由变化的自变量的个数,称为自由度),正如正态分布中均值或方差不同就是另一个正态分布一样,自由度不同就是另一个分布。记为 分布的均值为自由度 n,记为 E() = n;分布的方差为2倍的自由度(2n),记为 D() = 2n。
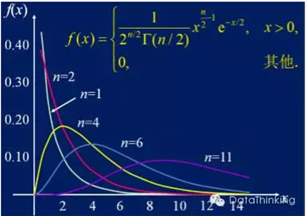
从分布图可以看出:分布在第一象限内,卡方值都是正值,呈正偏态(右偏态),随着参数 n 的增大,分布趋近于正态分布;随着自由度n的增大,分布向正无穷方向延伸(因为均值n越来越大),分布曲线也越来越低阔(因为方差2n越来越大)。