Problem Description
The series, 11 + 22 + 33 + ... + 1010 = 10405071317.
Find the last ten digits of the series, 11 + 22 + 33 + ... + 10001000.
Python
This problem is so easy to python, because python supports big integer~!
def Power(num, exp): result = 1; for i in xrange(exp): result = result * num return result def Problem_48(): result = 0 for n in xrange(1000): result = result + Power(n+1, n+1) print result Problem_48()
C++
It is much more complex to C++, especially you don’t have a big integer class or something alike.
You have to do everything on your own.
Since the problem require us to give the last ten digits of the sum, we just put our focus on the last ten digits.
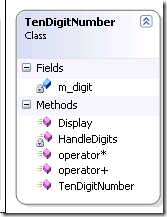
TenDigitNumber
First, I implement a class which only stores and handles last ten digits of a integer.
this class is very simple, the class diagram:
- Use “long m_digit[10]” to store the digits;
- Override “*” and “+” operator
- Method “Display” is used to print digits
To make it easier to explain the multiplication between two TenDigitnumber objects, I reduce digit count from 10 to 3, namely, how does a 3-digit number multiply another 3-digit number?
foe example, 123* 456 = ???, the diagram below interprets the approach of multiplication.
| 1 | 2 | 3 | ||
| 4 | 5 | 6 | ||
| 6 | 12 | 18 | ||
| 5 | 10 | 15 | ||
| 4 | 8 | 12 | ||
| 4 | 13 | 28 | 27 | 18 |
| 5 | 6 | 0 | 8 | 8 |
It is hard for me that using words to explain the steps, so present the codes:
TenDigitNumber operator *(const TenDigitNumber& other)
{
TenDigitNumber result(0);
for(int i=0; i<10; i++)
{
if(other.m_digit[i] == 0)
continue;
for(int j=0; j<10; j++)
{
if(i + j > 9)
break;
if(m_digit[j] == 0)
continue;
result.m_digit[i + j] += m_digit[j] * other.m_digit[i];
}
}
result.HandleDigits();
return result;
}
Addition is similar.
TenDigitNumber operator +(const TenDigitNumber& other)
{
TenDigitNumber result(0);
for(int i=0; i<10; i++)
{
result.m_digit[i] = m_digit[i] + other.m_digit[i];
}
result.HandleDigits();
return result;
}
HandleDigit method
void HandleDigits()
{
for(int i=0; i<10; i++)
{
if(m_digit[i] < 10 )
continue;
long temp = m_digit[i];
m_digit[i]=temp % 10;
temp = temp / 10;
if(i < 9)
m_digit[i+1] += temp;
}
}
Power Method
With TenDigitNumber, we can easily implement power method.
TenDigitNumber Power(int num, int exp)
{
TenDigitNumber tn(num);
TenDigitNumber result(1);
for(int i=0; i<exp; i++)
{
// result.Display();
result = result * tn;
}
return result;
}
Main method
void Problem_48()
{
TenDigitNumber result(0);
for(int i=1; i<=1000; i++)
{
TenDigitNumber temp = Power(i, i);
result = result + temp;
}
result.Display();
}