题目链接:https://www.luogu.com.cn/problem/P5682
题目描述
Alice 有 (n) 个正整数,数字从 (1 sim n) 编号,分别为 (a_1,a_2, cdots , a_n)。
Bob 刚学习取模运算,于是便拿这 (n) 个数进行练习,他写下了所有
(a_i) mod (a_j (1 le i,j le n wedge i eq j))
的值,其中 mod 表示取模运算。
Alice 想知道所有的结果中,严格次大值是多少。将取模后得到的所有值进行去重,即相同的结果数值只保留一个,剩余数中第二大的值就称为严格次大值。
解题思路
首先我们要排除无关因素带来的影响。
这里很明显的一个无关因素就是重复的元素。
我们假设存在 (a_i = a_j) 且 (i eq j),则对于任何一个 (k eq i wedge k eq j):
- (a[i]) mod (a[k] = a[j]) mod (a[k])
- (a[k]) mod (a[i] = a[k]) mod (a[j])
所以数值相同的两个元素是等价的。
我们可以给 (a1) 到 (a_n) 从小到大排序并去重。
我们假设去重后还剩下 (m) 个元素,且这些元素满足 (a_1 lt a_2 cdots lt a_m)。
则我们可以分 (m=1)、(m=2)、(m gt 2) 三种情况分开讨论:
m = 1
当 (m=1) 时,数组中只有一个元素:
- 如果 (n = 1),则不存在答案,输出 (-1);
- 如果 (n gt 1),则说明数组中所有的元素都是相同的,则任意 (a_i) mod (a_j) 的结果都是 (0),所以只存在一个最大值 (0),不存在次大值,同样也输出 (-1)。
m = 2
当 (m=2) 时,只有两个候选答案 (a_1) mod (a_2) 和 (a_2) mod (a_1),又因为 (a_1) mod (a_2 = a_1),(a_2) mod (a_1 lt a_1)(余数必然小于除数),所以次大值肯定是 (a_2) mod (a_1)。
m > 2
当 (m gt 2) 时,可以确定的是最大值是 (a_{m-1}) mod (a_m)。
次大值应该是以下两者的较大值:
- (a_{m-2}) mod (a_m);
- (a_{m}) mod (a_{m-1})。
详细证明
为了方便讲述起见,我接下来用 (a \% b) 来表示 (a) mod (b),并且我们这里只证明 (m gt 2) 的情况。
这里有一个非常重要的基础性质:
性质1:余数永远小于除数!
我们接下来会反复运用到这个性质1进行分析。
首先我们证明 (a_{m-1} \% a_m) 是最大值。
因为 (a_{m-1} \% a_m = a_{m-1})。
证:
我们把 (a_i \% a_j) 的组合分为 (2) 部分:
第一部分:(j=m)
此时 (i in [1, m-1]),
(a_1 \% a_m lt a_2 \%a_m lt cdots lt a_{m-1} \% a_m)
所以第一部分的最大值是 (a_{m-1} \% a_m = a_{m-1})
第二部分:(j
eq m),
此时,除数最大是 (a_{m-1}),根据性质1,可得:这一部分的所有答案都小于 (a_{m-1})。
据此可得:最大值即为 (a_{m-1} \% a_m = a_{m-1})。
其次我们要求次大值
次大值其实就是除了 (a_{m-1}) 以外的最大值。
第一部分里面除了 (a_{m-1} \% a_m) 以外的最大值就是 (a_{m-2} % a_m = a_{m-2}) 了。
第二部分我们可以将它拆分成两小部分:
第2.1部分:(j = m-1) 的部分,这一部分的是 (a_{m-2}) 和 (a_m \% a_{m-1}) 的较大值;
第2.2部分:(j le m-2) 的部分,根据性质1,这一部分的所有答案都 (lt a_{m-2})。
综上所述,我们可以发现,次大值的竞争者只有 (2) 个值:(a_{m-2}) 或者 (a_m \% a_{m-1})。
所以此时次大值即为 (max(a_{m-2}, a_m \% a_{m-1}))。
另附上一张图片方便理解:
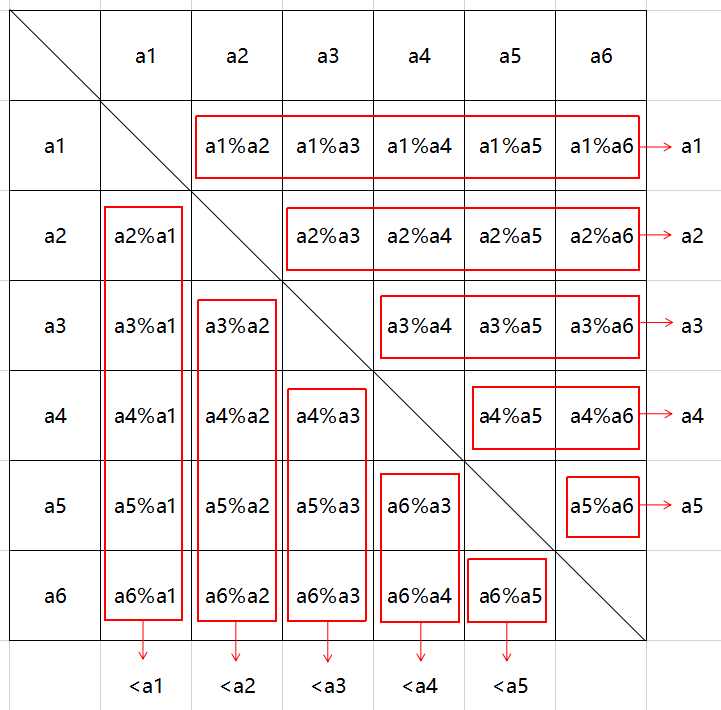
实现代码如下:
#include <bits/stdc++.h>
using namespace std;
const int maxn = 200020;
int n, m, a[maxn], ans;
int main() {
cin >> n;
for (int i = 1; i <= n; i ++) cin >> a[i];
sort(a+1, a+1+n);
m = unique(a+1, a+1+n) - a - 1;
if (m == 1) ans = -1;
else if (m == 2) ans = a[2] % a[1];
else ans = max(a[m-2] % a[m], a[m] % a[m-1]);
cout << ans << endl;
return 0;
}