题目描述
给出一个无向图,求出最小生成树
输入输出格式
输入格式:
第一行包含两个整数N、M,表示该图共有N个结点和M条无向边。(N<=5000,M<=200000)
接下来M行每行包含三个整数Xi、Yi、Zi,表示有一条长度为Zi的无向边连接结点Xi、Yi
输出格式:
输出包含一个数,即最小生成树的各边的长度之和
输入输出样例
说明
时空限制:1000ms,128M
数据规模:
对于20%的数据:N<=5,M<=20
对于40%的数据:N<=50,M<=2500
对于70%的数据:N<=500,M<=10000
对于100%的数据:N<=5000,M<=200000
样例解释:
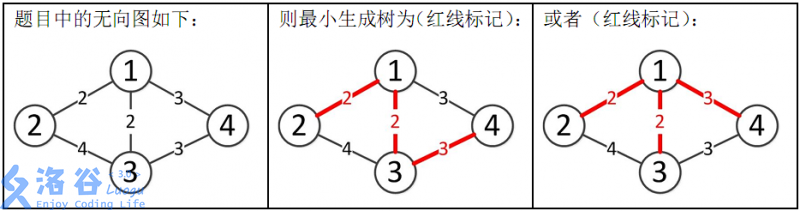
所以最小生成树的总边权为2+2+3=7
算法 1 :Kruskal
这个算法与求最短路的 dij 算法非常像,不同处只有一行
送一个额外的样例:
5 18
2 4 276
3 3 435
3 4 608
2 4 860
1 2 318
1 3 547
5 4 419
2 5 98
1 5 460
5 3 399
3 5 240
3 2 733
3 3 903
4 2 909
5 2 206
3 4 810
2 1 115
2 3 419
ans=729
调了 n 便的代码(有些独流题两点之间会有多条道路,一定要取 min !!!)
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int MX=5010;
int n,m,f[MX][MX],dis[MX];
bool vis[MX];
void prim()
{
memset(dis,0x3f,sizeof(dis));
dis[1]=0;
for(int i=1;i<=n;++i)
{
int pos=0;
for(int j=1;j<=n;++j)
if((!vis[j]) && dis[j]<dis[pos])
pos=j;
if(pos==0)break;
vis[pos]=1;
for(int j=1;j<=n;++j)
if( !vis[j] && f[pos][j]<dis[j]) dis[j]=f[pos][j];
}
}
int main()
{
scanf("%d%d",&n,&m);
memset(f,0x3f,sizeof(f));
for(int i=1;i<=m;++i)
{
int from,to,val;
scanf("%d%d%d",&from,&to,&val);
f[from][to]=f[to][from]=min(f[from][to],val);
}
prim();
int t=0;
for(int i=1;i<=n;++i)
t+=dis[i];
printf("%d",t);
return 0;
}
算法 2:Prim
这个是一个非常简单暴力的算法,既然要求最小生成树,那所取的边必然是所有边排完序(升序),不断地从小取到大,直到取到 n-1 条(树的性质)
如果每两点只有一条边,上述操作已经可以了
但就是有些独流题目(比如这道),不止一条,我们就需要用并查集来记录是否已连接,还可以防止成环哦~(感觉并不需要)
其实用 vis 的一个二维数组也可以,但占用空间过大(数据点小还是挺方便的)
代码^-^
#include<stdio.h> #include<algorithm> using namespace std; const int MX=5010; struct Edge { int x,y,val; }edge[200001]; int n,m,ans,cnt,fa[MX]; bool operator<(Edge a,Edge b) { return a.val<b.val; } int Get(int x){ if(x==fa[x]) return x; return fa[x]=Get(fa[x]); } int main() { scanf("%d%d",&n,&m); for(int i=1;i<=m;++i){ scanf("%d%d%d",&edge[i].x,&edge[i].y,&edge[i].val); } sort(edge+1,edge+1+m); for(int i=1;i<=n;++i) fa[i]=i; for(int i=1;i<=m;++i) { int x=Get(edge[i].x); int y=Get(edge[i].y); if(x==y) continue; fa[x]=y; ans+=edge[i].val; if(++cnt==n-1) break; } printf("%d",ans); return 0; }