E. Alyona and Triangles
题目连接:
http://codeforces.com/contest/682/problem/E
Description
You are given n points with integer coordinates on the plane. Points are given in a way such that there is no triangle, formed by any three of these n points, which area exceeds S.
Alyona tried to construct a triangle with integer coordinates, which contains all n points and which area doesn't exceed 4S, but, by obvious reason, had no success in that. Please help Alyona construct such triangle. Please note that vertices of resulting triangle are not necessarily chosen from n given points.
Input
In the first line of the input two integers n and S (3 ≤ n ≤ 5000, 1 ≤ S ≤ 1018) are given — the number of points given and the upper bound value of any triangle's area, formed by any three of given n points.
The next n lines describes given points: ith of them consists of two integers xi and yi ( - 108 ≤ xi, yi ≤ 108) — coordinates of ith point.
It is guaranteed that there is at least one triple of points not lying on the same line.
Output
Print the coordinates of three points — vertices of a triangle which contains all n points and which area doesn't exceed 4S.
Coordinates of every triangle's vertex should be printed on a separate line, every coordinate pair should be separated by a single space. Coordinates should be an integers not exceeding 109 by absolute value.
It is guaranteed that there is at least one desired triangle. If there is more than one answer, print any of them.
Sample Input
4 1
0 0
1 0
0 1
1 1
Sample Output
-1 0
2 0
0 2
Hint
题意
给你n个点,保证覆盖的面积不超过S。
你需要找到一个面积小于4S的三角形,使得这个三角形包含了所有的点。
题解:
有一个结论,需要猜一下。
就是我其实就是找到这个n个点,中选择三个点组成的最大三角形。
找到这个三角形之后,通过旋转和放大之后,就可以得到我要的答案了。
如图:(来自Quailty的图)
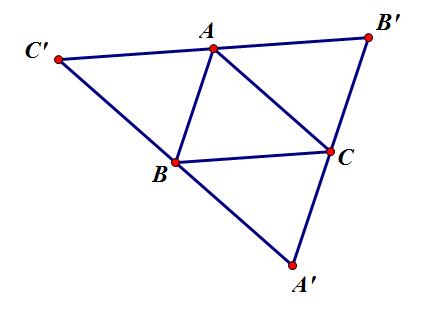
证明也比较简单,这里略掉。
这个怎么做呢?经典题:http://www.spoj.com/problems/MTRIAREA/
其实随机化也可以,但是我不知道随机化是否能被卡掉,因为这道题要求并不是最优的……
代码
#include<bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<long long,long long> node;
long long cross(node a,node b,node c)
{
return abs((b.x-a.x)*(c.y-a.y)-(b.y-a.y)*(c.x-a.x));
}
vector<node>P;
int n;
long long s;
int main()
{
cin>>n>>s;
for(int i=1;i<=n;i++)
{
node p;
scanf("%lld%lld",&p.x,&p.y);
P.push_back(p);
}
sort(P.begin(),P.end());
P.erase(unique(P.begin(),P.end()),P.end());
node a,b,c;
a=P[0],b=P[1],c=P[2];
long long ans = cross(a,b,c);
int flag = 1;
while(flag)
{
flag = 0;
random_shuffle(P.begin(),P.end());
for(int i=0;i<P.size();i++)
{
long long tmp = cross(P[i],b,c);
if(tmp>ans)
{
ans=tmp;
a=P[i];
flag=1;
}
}
for(int i=0;i<P.size();i++)
{
long long tmp = cross(a,P[i],c);
if(tmp>ans)
{
ans=tmp;
b=P[i];
flag=1;
}
}
for(int i=0;i<P.size();i++)
{
long long tmp = cross(a,b,P[i]);
if(tmp>ans)
{
ans=tmp;
c=P[i];
flag=1;
}
}
}
cout<<a.x+b.x-c.x<<" "<<a.y+b.y-c.y<<endl;
cout<<a.x+c.x-b.x<<" "<<a.y+c.y-b.y<<endl;
cout<<b.x+c.x-a.x<<" "<<b.y+c.y-a.y<<endl;
}