马拉车算法详解

简述

　　Manacher算法，又称马拉车算法，它是用于求一个字符串的最长回文子串长度的算法，时间和空间复杂度为O(n)。

算法思想

　　求一个字符串的最长回文子串长度，我们如果用暴力来做，我们就要取出这个串的所有子串，然后判断这个子串是不是回文串，复杂度是n方的。

　　那么马拉车为何如此神奇能做到O(n)呢？

　　首先我们来看这两个串：abba和abcba。第一个串的回文中心在两个b之间，第二个串的回文中心为字符c，这样两种情况我们分类讨论太麻烦了，所以我们考虑对原字符串进行一个字符填充，abba->@#a#b#b#a# ，abcba->@#a#b#c#b#a#，这样他们都变成了奇数，讨论的情况就一致了。

　　设原字符串长度为len1，重构后长度为len2，则len2=len1*2+2且对于s[i]，它在重构后字符串的对应下标为i*2+2。

　　由此我们可以写出重定义字符串的代码：

int getstr()
{//重定义字符串，s为原字符串，str为新串,len为s串长度,返回新串长度 
    int k=0,len=strlen(s);
    str[k++]='@';
    for(int i=0;i<len;i++){
        str[k++]='#';
        str[k++]=s[i];
    } 
    str[k++]='#';
    return k;
}

　　首先我们规定几个变量的含义：len[i]为以i为中心点的最长回文序列的回文半径，po为当前中心点，p为当前回文子串的右边界。　　

　　我们可以得出，ans=len[i]-1，因为加入填充字符后的str的最长回文串为2*len[i]-1，又因为#号的个数比原字符多一个，所以#字符的总数为len[i]个，故原字符的最长回文子串为len[i]-1个。

　　当i<=p时，找到i相对于po的对称点j，如果len[j]<p-i,如下图：

　　

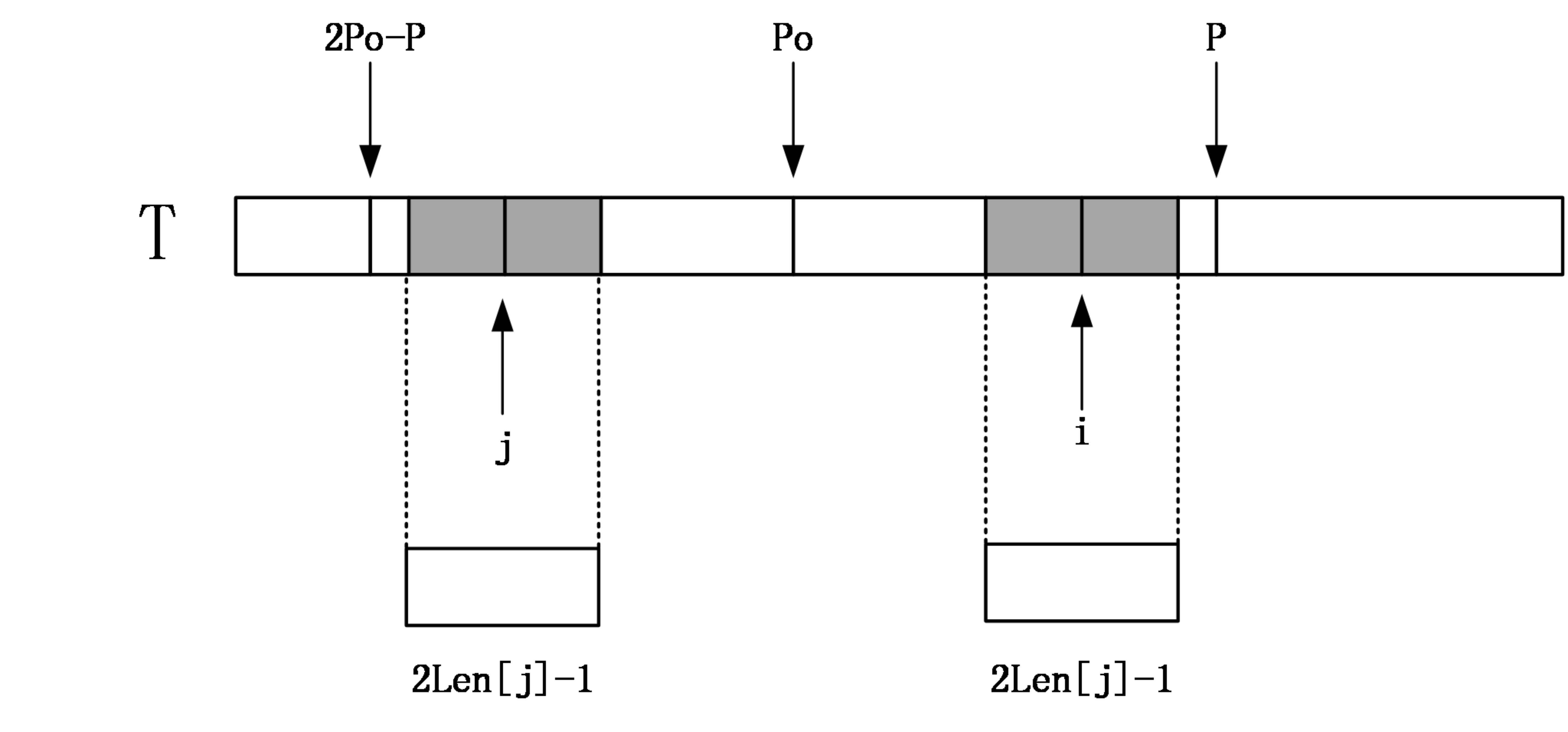
　　由对称性得知，i和j左右的字符是一样的，所以len[i]=len[j]。

　　如果len[j]>=p-i，由对称性，说明以i为中心的回文串会扩散至p以外，而大于p部分的串我们还没用匹配，所以我们一个一个匹配，更新po和len[i]。

　　

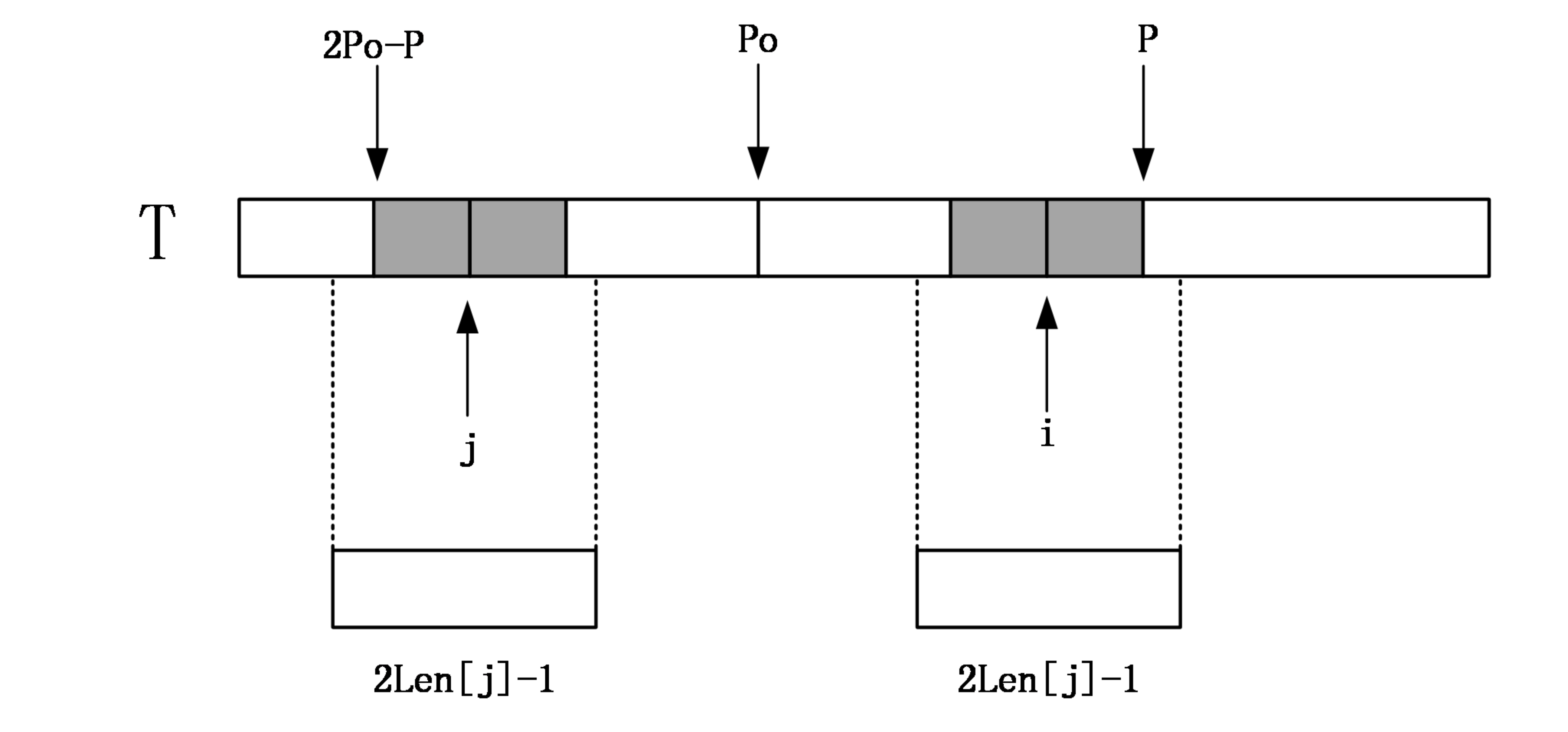
　　当i>p时，说明以i为中心的回文串一点都没匹配，就只能老老实实一个一个匹配了。

　　

　　所以我们可以写出如下匹配部分代码：

int manacher(int len){//len为str串长度 
    int mx=0,id;
    int maxx=0;
    for(int i=0;i<len;i++){
        if(i<mx) num[i]=min(mx-i,num[2*id-i]);//i在mx左边，取在边界以内且较小的那段 
        else num[i]=1;//i在mx右边，所以直接等于1 
        while(str[i+num[i]]==str[i-num[i]]) num[i]++;//向右一个个匹配 
        if(i+num[i]>mx){
            mx=i+num[i];
            id=i;
            maxx=max(maxx,num[i]-1);
        }
    }
    return maxx;
}

模板

#include<iostream>
#include<string.h> 
using namespace std;
const int maxn=11000002;
char s[maxn<<1],str[maxn<<1];
int num[maxn*2];
int getstr()
{
    int k=0,len=strlen(s);
    str[k++]='@';
    for(int i=0;i<len;i++){
        str[k++]='#';
        str[k++]=s[i];
    } 
    str[k++]='#';
    return k;
}
int manacher(int len){
    int mx=0,id;
    int maxx=0;
    for(int i=0;i<len;i++){
        if(i<mx) num[i]=min(mx-i,num[2*id-i]);
        else num[i]=1;
        while(str[i+num[i]]==str[i-num[i]]) num[i]++;
        if(i+num[i]>mx){
            mx=i+num[i];
            id=i;
            maxx=max(maxx,num[i]-1);
        }
    }
    return maxx;
} 
int main()
{
    int cas=1;
    while(cin>>s){
        if(s[0]=='E') break;
        int len1=strlen(s);
        int len2=getstr();
        cout<<"Case "<<cas++<<": "<<manacher(len2)<<'
';
    } 
    return 0;
}