树状数组相比线段树来说比较简单,可以快速的进行区间求和和单点修改,当然,如果利用辅助数组,还可以进行区间修改
浅谈“树状”
这是一颗满二叉树:

只要让所有的节点向右靠近,就得到树状数组的样子
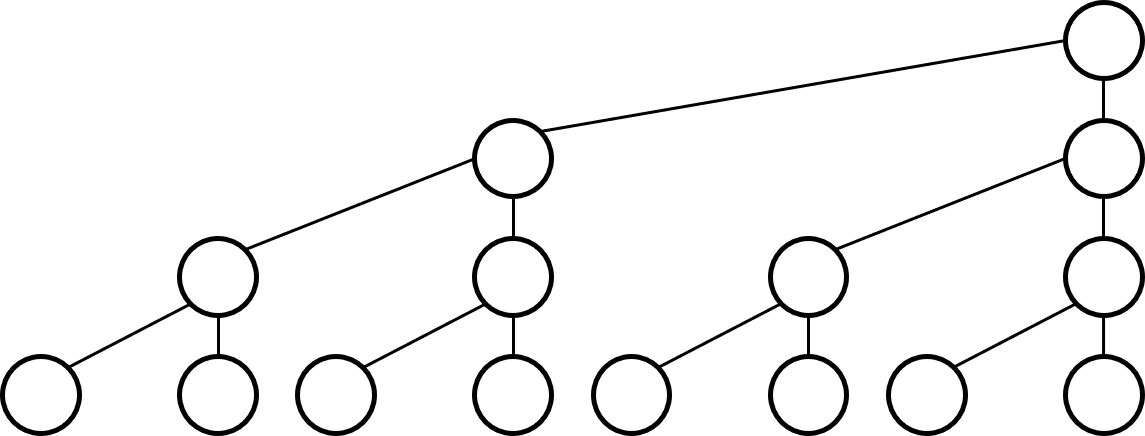
树状数组存值的方式如下,其中nu数组是一段初始序列,t数组是树状数组
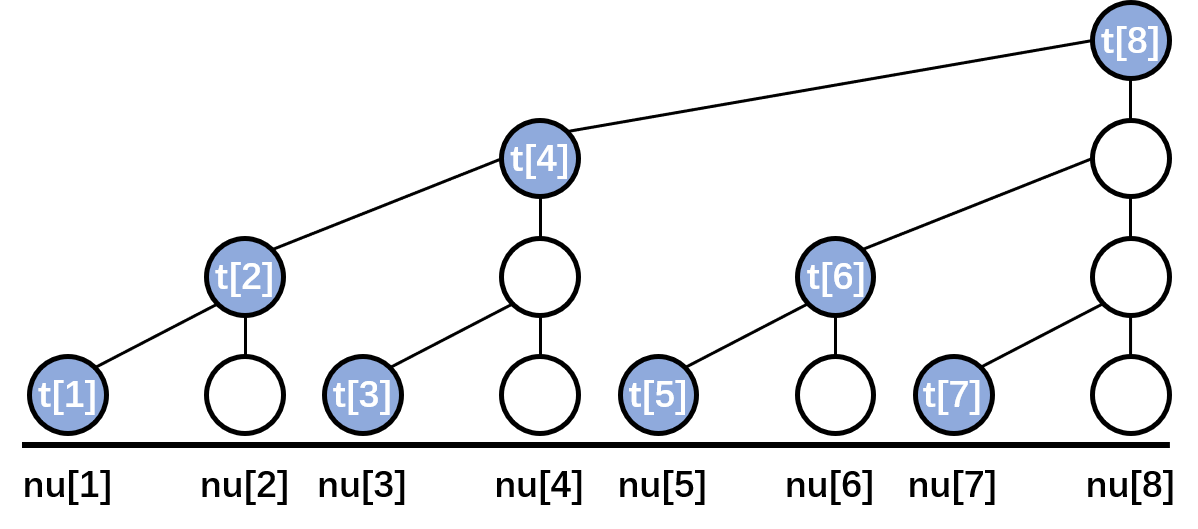
根据二叉树每两个节点都有一个父亲节点的性质可知,nu数组与t树状数组有以下对应关系:
t[1]=nu[1]
t[2]=nu[1]+nu[2]
t[3]=nu[3]
t[4]=nu[1]+nu[2]+nu[3]+nu[4]
t[5]=nu[5]
t[6]=nu[5]+nu[6]
t[7]=nu[7]
t[8]=nu[1]+nu[2]+nu[3]+nu[4]+nu[5]+nu[6]+nu[7]+nu[8]
......(nu序列越长,树的高度就变高)
看到这里,想必已经发现了,树状数组t可以很好的用来查询nu数组的区间和,紧接着就来介绍对应关系的规律
树状数组的存值规律与lowerbit函数
规律一:
对于任意一个树状数组t[n],一定包括了初始序列中的nu[n]元素的值
这个规律可以通过观察二叉树的模式以及上述例子中的规律可以看出。
规律二:
规律二需要细讲。
对于任意一个n,我们可以观察n的二进制数的表达形式,比如:
当n=5时,n的二进制数为101,可以观察到,5的二进制数最靠近末尾的1(高亮)代表的值为10进制中的1
再比如:
当n=6时,n的二进制数为110,可以观察到,6的二进制数最靠近末尾的1(高亮)代表的值为10进制中的2
当n=8时,n的二进制数为1000,可以观察到,8的二进制数最靠近末尾的1(高亮)代表的值为10进制中的8
即:
假设n的二进制数最靠近末尾的1代表10进制中的数m,则树状数组t[n]存有初始序列nu中连续的m个数,且以nu[n]为连续m个数中的最后一个数。
为了得到n的二进制数最靠近末尾的1代表10进制中的数m,可以利用对应n的负数二进制来表示
假设n=6,对应-6原码为10000000 00000000 00000000 00000110,反码为11111111 11111111 11111111 11111001
反码的补码(-6的二进制)为11111111 11111111 11111111 11111010,而6的二进制为00000000 00000000 00000000 00000110,则m=6&-6=2
于是诞生了lowerbit函数:
1 int lowerbit(int n){
2 return n&-n;
3 }
假设m=lowerbit(n),那么树状数组t[n]=nu[n]+nu[n-1]+....+nu[n-m+1](共m个数),记住初始序列nu和树状数组tr都是从下标为1开始的。
建树
听说树状数组还要建树?这又不是线段树,知道的人都直到树状数组根本不用建树,因为树状数组的本质就是数组。
我们可以将一个树状数组初始化全为0,每次将树状数组进行单点修改就行了。
maybe你将单点修改和区间求和看完之后,就很好理解树状数组是不需要建树的。
单-区形树状数组(单点修改--区间查询)(最基本的树状数组)
前言
单点修改--区间查询形树状数组是最基本的树状数组,可以通过创建树状数组t,来对初始序列nu进行单点修改和区间查询。
单点修改
单点修改如下图所示,假设将nu[5]加上一个$\Delta$t之后,对应的t[5],t[6],t[8]都要加上一个$\Delta$t
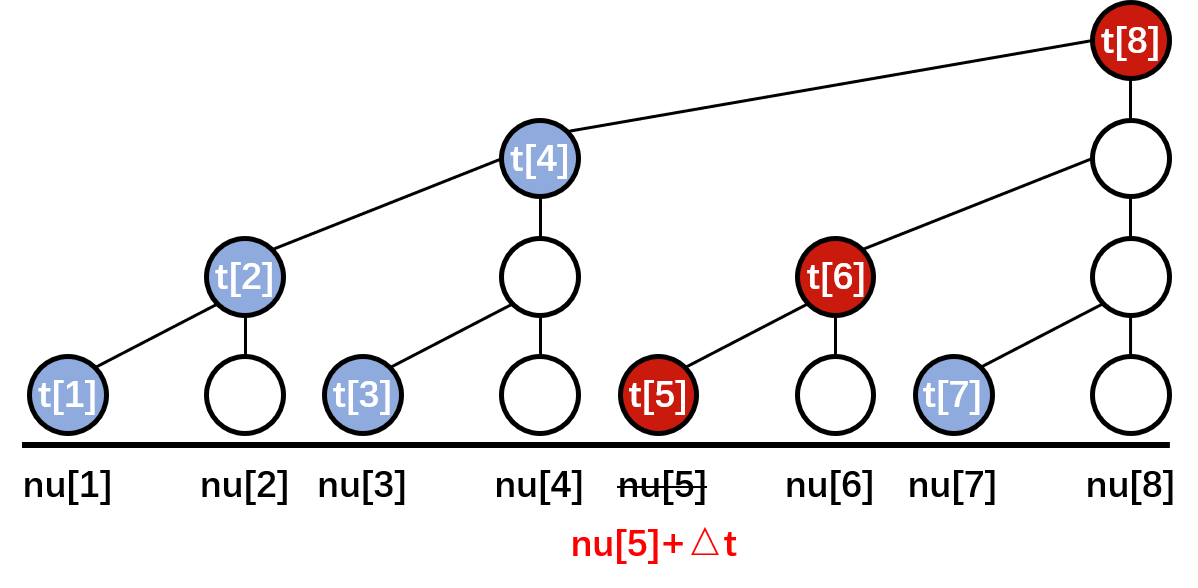
那么,当修改了nu[n]时,不仅要修改树状数组t[n]节点,还需要修改t[n]所有向上的节点(图中红色节点),如何找到t[n]向上节点的下标值?
回答:我们发现一个规律,树状数组t[n]向上的第一个节点(父亲节点)即为t[n+lowerbit(n)]节点,像这样不断向上修改,直到n>MAXn
当我们修改了nu[1]时,紧接着修改t[1]节点:
此时n=1,lowerbit(1)=1,1+lowerbit(1)=2,于是还要修改t[2]节点;
此时n=2,lowerbit(2)=2,2+lowerbit(2)=4,于是还要修改t[4]节点;
此时n=4,lowerbit(4)=4,4+lowerbit(4)=8,于是还要修改t[8]节点;
修改完毕。
下面是单点修改代码,其中tr[]是树状数组,n是要修改的nu[n]的下标,mv是$\Delta$t
1 void add(long long tr[],long long n,long long mv){
2 for(long long i=n;i<=maxn;i+=lowerbit(i))
3 tr[i]=(tr[i]+mv);
4 return;
5 }
从单点修改也可以看出为什么树状数组的初始序列的下标要从1开始,如果从0开始的话,lowerbit(0)=0,0+0=0,这样单点修改的程序将一直循环下去。
区间查询
说明:树状最普通的区间求和方法只能求nu[1]到nu[n]的和,假如你要求t[m]到t[n]的和,可以先求出nu1]到nu[n]之和以及nu[1]到nu[m-1]之和,两个区间和相减即是t[m]到t[n]之和。
如图,下图即是求nu[1]至nu[6]之和:
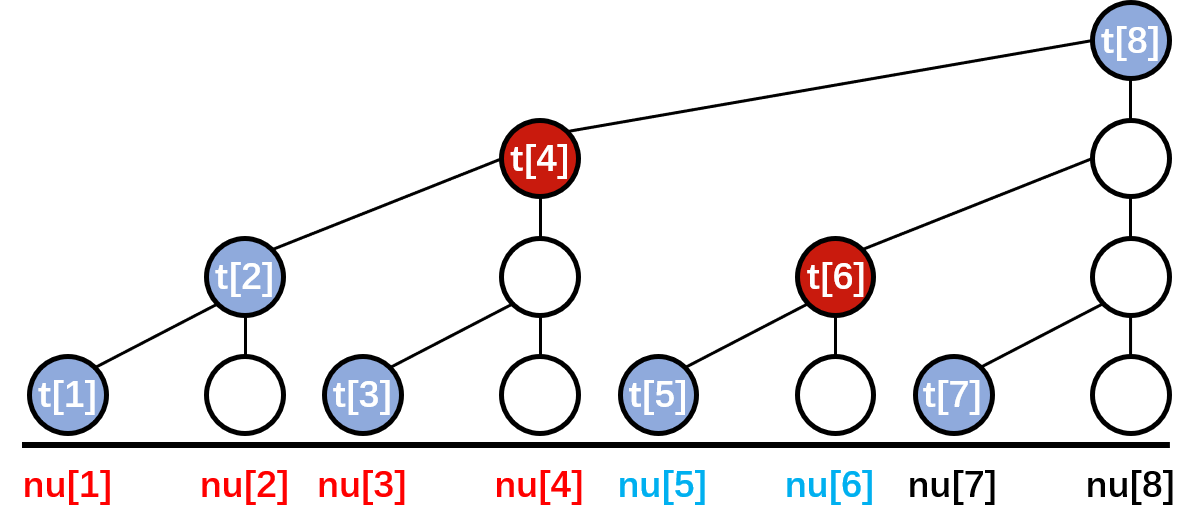
t[4]=nu[1]+nu[2]+nu[3]+nu[4]
t[6]=nu[5]+nu[6]
故t[4]+t[6]就是nu[1]到nu[6]之和,在这里也有规律。
假如要求nu[1]到nu[n]之和,和一定包括且大于等于t[n],可以发现,除了t[n],t[n-lowerbit(n)]也包括在和之中,以此类推,假如和包括t[n],那么也包括t[n-lowerbit[n]],这样循环下去,直到n=0
要求nu[1]到nu[5]之和,先将sum初始化为0:
sum+=t[5],此时n=5,lowerbit(5)=1,5-lowerbit(5)=4;
sum+=t[4],此时n=4,lowerbit(4)=4,4-lowerbit(4)=0;
结束求和。
下面是区间查询代码,tr[]是树状数组,n代表需要从nu[1]求和到nu[n]
1 long long sum(ll tr[],int n){
2 long long sum=0;
3 for(int i=n;i>0;i-=lowerbit(i))
4 sum+=tr[i];
5 return sum;
6 }
区-单形树状数组(区间修改--单点查询)
前言
区间修改--单点查询形树状数组并不是维护初始序列,而是维护初始序列的差分序列,此时区间修改和单点查询的复杂度就大大降低。区-单形树状数组是单-区形的变形体。
差分序列
假设一个初始序列(初始数组)nu为nu[1],nu[2],nu[3]....nun],如果存在一个序列x,使得
x[1]=nu1]-nu0]=nu[1](nu[0]=0)
x[2]=nu[2]-nu[1]
x[3]=nu[3]-nu[2]
....
x[n-1]=nu[n-1]-nu[n-2]
x[n]=nu[n]-nu[n-1]
那么称序列x为初始序列nu的差分序列,用单-区形树状数组维护初始序列的差分序列可以得到区-单形树状数组。
单点查询
用树状数组t维护初始数组nu的的差分序列x,那么单点查询初始序列nu的值有两种方法:
1.直接对初始序列nu进行查询
比如要查询nu[n]的值,直接查询就行了。(最弱智的方法)
ps:用这个方法的前提是你压根就没有使用树状数组进行维护!!
2.利用树状数组t(我本人觉得多此一举)
利用差分数组的性质(x[n]=nu[n]-nu[n-1]),可以得到
x[n]+x[n-1]+x[n-2]+...+x[1]=nu[n]-nu[n-1]+nu[n-1]-nu[n-2]+nu[n-2]-nu[n-3]+...+nu[1]=nu[n]
所以树状数组t进行区间查询差分序列x相当于单点查询初始序列nu(可这有什么意义吗?)
好吧,其实意义大得很:当然,如果一开始肯定觉得这个单点查询的方法多此一举,但是如果我们想要进行区间修改,我们并不是直接修改初始序列nu,我们每一次修改都是在维护树状数组t,所以,对于每一次修改,修改的只是树状数组,所以一旦进行了修改操作,初始序列的值并没有发生改变,于是我们每一次查询就只能针对树状数组t来实现了。
区间修改
不多说,上图,如图,这是一个初始序列nu(柱状图代表值)

其中nu为初始序列,x为差分序列,即x[n]=nu[n]-nu[n-1],假设nu序列里元素刚开始全部相同(所以说柱状图长度相同),则x序列元素全为0.
当我们将初始序列nu的某一个区间内全部元素加上t,如图所示:
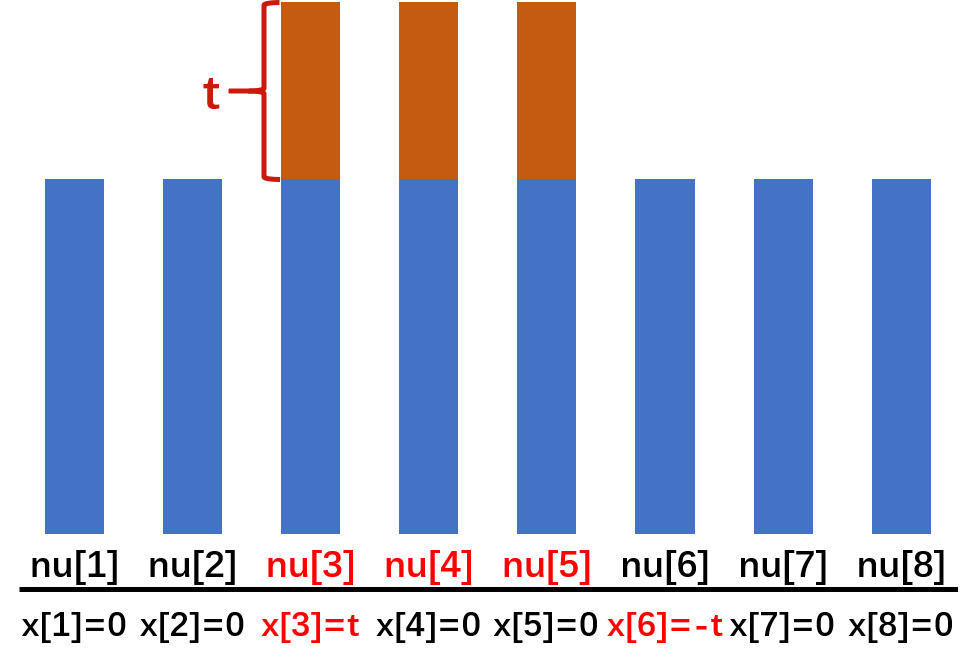
从图中可以发现,虽然初始序列nu一个区间内的值全部被改变了,但是对于差分序列x,只有两个值被改变了(高亮显示)
由此,可以推广出:
如果初始序列nu的某一个区间nu[n]到nu[m]的所有值全部加上t,则相当于单点修改差分序列x(x[n]=x[n]+t,x[m+1]=x[m+1]-t),用树状数组维护差分序列x就行了。
后言
的确,维护差分序列有一点麻烦,因为我们一开始只有初始序列,所以为了维护差分序列,我们还要对树状数组进行预处理,即一开始就要对树状数组进行单点修改,使得树状数组存有初始序列的差分差分序列
ps:如果你发现题目中的区间修改,只是在原有数值的基础上加上或者减去一个t,你可以尝试用树状数组,但是如果题目中的修改指的是直接用新的值赋给区间的旧值,那么最好别尝试使用树状数组!!
区-区形树状数组(区间修改--区间查询)
前言
区间修改--区间查询形树状数组则又是区-单形的变形体,它与区-单形具有同一种区间修改的方法,唯一多的就是区-区形特有的区间查询。
区间修改
和区-单形同样使用维护初始序列的差分序列进行区间修改,详细内容请移步区-单形树状数组的区间查询(右上角目录)。
区间查询
这里我们需要思考一下,假设我们想求初始序列nu[1]+nu[2]+...nu[n]的值,前面提到过的差分序列x,即nu[n]=x[1]+x[2]+x[3]+...+x[n].
故:
$nu[1]+nu[2]+...nu[n]$
$=x[1]+(x[1]+x[2])+(x[1]+x[2]+x[3])+...+(x[1]+x[2]+x[3]+...+x[n])$
$=n*(x[1]+x[2]+x[3]+...+x[n])-[(n-1)*x[n]+...+2*x[3]+1*x[2]]$
$=n*\sum^{n}_{i=1}x[i]-\sum^{n}_{i=1}(i-1)*x[i]$
于是,只用维护两个树状数组,一个维护差分序列x[n]树状数组,一个维护(n-1)*x[n]树状数组,x[n]的前n项和sumx乘上n减去(n-1)*x[n]的前n项和就是初始序列的前n项和。
二维树状数组
单-区形二维树状数组(单点修改--区间查询)
与一维树状数组不同的是,二维树状数组需要考虑x,y两个变量,但是储存规律和一维的相同,只需在单点修改和区间查询的的操作中再套上一个循环即可。
假设初始二维序列是nu[n][m],二维树状树状数组是tree[n][m],那么tree[x][y]存的是二维初始序列中右下角为nu[x][y],宽lowerbit(y),高为lowerbit(x)的子区间的区间和。
单点修改代码:
void add(int x,int y,int z){ int i,j; for(i=x;i<=n;i+=lowerbit(i)) for(j=y;j<=n;j+=lowerbit(j)) tree[i][j]+=z; return; }
区间查询(从nu[1][1]到nu[x][y])代码:
int sum(int x,int y){ int i,j; int sum=0; for(i=x;i>0;i-=lowerbit(i)) for(j=y;j>0;j-=lowerbit(j)) sum+=tree[i][j]; return sum; }
那么,初始序列从nu[x1][y1]到nu[x2][y2]的子区间和为
sum(x2,y2)-sum(x2,y1-1)-sum(x1-1,y2)+sum(x1-1,y1-1)
区-单形二维树状数组(区间修改--单点查询)
如同区-单形一维数组一样,区-单形二维数组维护的也是初始序列的差分序列,二维初始序列的差分序列如图所示
若二维初始序列是nu[m][n],则对应初始序列的差分序列$x[a][b]=nu[a][b]+nu[a-1][b-1]-nu[a-1][b]-nu[a][b-1]$
如下图所示:
\begin{bmatrix}2 & 1 & 3\\6 & 5 & 4\\7 & 9 & 8\end{bmatrix} 对应差分序列x为 \begin{bmatrix}2 & -1 & 2\\4 & 0 & -3\\1 & 3 & 0\end{bmatrix}
因此,对于单点查询来说,$nu[x][y]=\sum^{x}_{i=1}\sum^{y}_{j=1}x[i][j]=sum[x][y]$
对于区间修改,我们先看下面的例子

将nu[2][2]到nu[3][3]区间全部加1之后得到
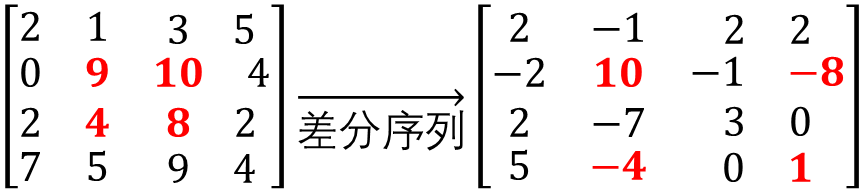
于是得到一个规律,如果把初始序列从nu[x1][y1]到nu[x2][y2]全部加上x,则对于差分序列x的x[x1][y1]和x[x2+1][y2+1]要加上x,x[x2+1][y1]和x[x1][y2+1]要减去

后言
树状数组虽好,但是要注意:
1.如果题目中的描述只存在单点修改和区间查询的话,可以放心大胆的用树状数组。
2.如果题目中的描述存在单点查询和区间修改,且区间修改只是在原有值的基础上加上或者减去一个值,那么也可以用树状数组;如果区间修改指的是区间重新赋值,那么不能用树状数组,可以用线段树。
3.如果题目描述中存在区间修改和区间查询,同上。
4.如果题目中啥都有,建议用线段树,这样的复杂度可能小一些。
在一般的比赛中,通常不会只存在线树状数组解题的题目,一般来说,树状数组是是配合离散化或者dp,离线等解题的工具,有时候仅仅是寻找需要如何使用树状数组的也有一些难度。
总结代码
ps:板子的变量名想换就换,像树状数组tr[]和maxn都是全局变量。
lowerbit代码:

int lowerbit(int n){ return n&-n; }
单点修改代码:

void add(long long tr[],long long n,long long mv){
for(long long i=n;i<=maxn;i+=lowerbit(i))
tr[i]=(tr[i]+mv);
return;
}
使用说明:tr[]是树状数组,n是要修改的nu[n]的下标,mv是$\Delta$t
区间求和代码:

long long sum(ll tr[],int n){
long long sum=0;
for(int i=n;i>0;i-=lowerbit(i))
sum+=tr[i];
return sum;
}
使用说明:tr[]是树状数组,n代表需要从nu[1]求和到nu[n]
最后,可以看看某神犇的树状数组模板(传送门)
例题
1.牛客练习赛46----E-华华和奕奕学物理:https://blog.csdn.net/weixin_43702895/article/details/90758988
2.牛客练习赛48----C-小w的糖果:https://blog.csdn.net/weixin_43702895/article/details/94733481
