一、名称定义: 顾名思义,决策树是基于树的结构进行的一种决策
二、决策树的组成部分:
1. 根节点 (比如下图的“纹理”就是根节点)
2. 内部节点(比如下图的“根蒂”,“触感”等属性就是内部节点)
3. 叶节点(比如下图的“好瓜”、“坏瓜”等分类就是叶节点)
三、一般的决策过程:
决策过程就是对数据“属性”的“测试”过程,每个测试的考虑范围是在上一个决策的结果范围之内去考虑。 比如接下来的这个图:如果已经判断纹理清晰,则判断根蒂的时候是在纹理清晰的范围内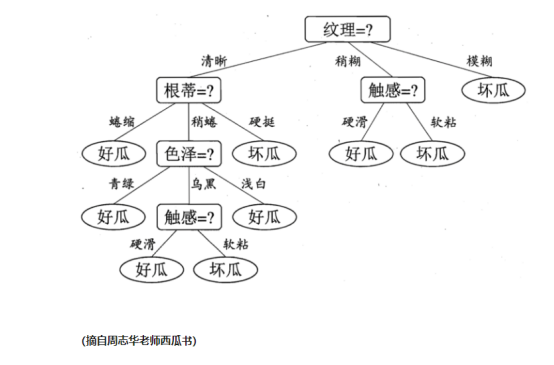
四、决策树的目的
决策树的目的是产生一颗泛化能力强的决策树(个人理解就是产生一个通用的决策模型)
五、决策树如何选择最优划分属性
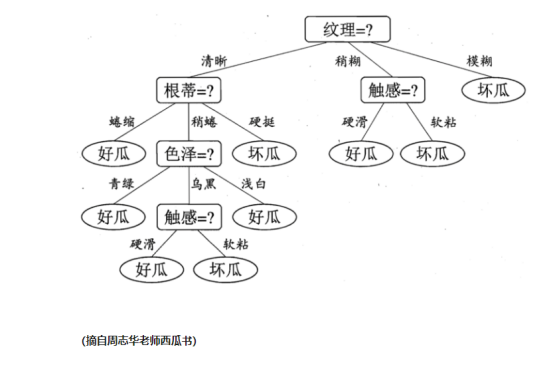
如上图所示(还是同一个图),可能大家会疑问,为什么我们的根节点是纹理,不是别的属性(根蒂,触感等属性表示不服),这就牵扯到最优划分属性这个概念。
最优划分属性:
顾名思义,用这个属性划分是最好的(到底什么最好呢),当然是节点纯度。在决策的时候还是希望节点包含的样本属于同一类(为了省时省力) 度量节点纯度的一个概念叫做“信息增益”
信息增益:
要想了解信息增益这个概念之前要先了解信息熵这个定义: 信息熵是用来表示样本集合纯度最常用的一种指标。(样本纯度就是字面意思,样本都是同一类就纯度高,信息熵的值就低)
信息熵的计算公式如下:
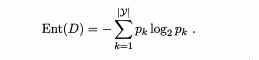
Pk 表示第K类样本在当前样本中所占的比例。y表示样本分类个数。
信息增益公式如下:
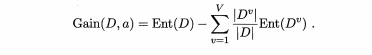
V表示属性a的几个可能值,比如触感有硬滑和软粘两种。Dv 则表的是在属性a的时候取得样本数。D表示所有样本个数。
信息增益例子:

图片数据来自西瓜书
从表可以看出好瓜占的比例是p1=8/17,坏瓜的比例 p2=9/17,可以计算出根节点的信息熵
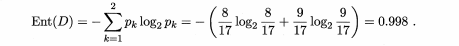
然后计算各个属性的信息增益:本例先计算色泽:由表可知色泽有三个取值:青绿、乌黑、浅白,然后样本根据这三个值进行划分。

(同样是截自西瓜书,主要是公式不好打)
然后计算出“色泽”的信息增益
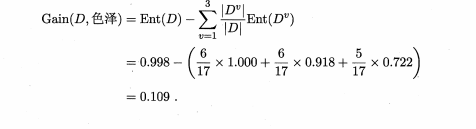
同理计算出其他属性的信息增益,最后比较得出纹理的最高。所以纹理首先对根节点进行划分。然后在划分之后,每个属性在根据新的样本进行划分。
决策树
一、名称定义: 顾名思义,决策树是基于树的结构进行的一种决策
二、决策树的组成部分:
1. 根节点 (比如下图的“纹理”就是根节点)
2. 内部节点(比如下图的“根蒂”,“触感”等属性就是内部节点)
3. 叶节点(比如下图的“好瓜”、“坏瓜”等分类就是叶节点)
三、一般的决策过程:
决策过程就是对数据“属性”的“测试”过程,每个测试的考虑范围是在上一个决策的结果范围之内去考虑。 比如接下来的这个图:如果已经判断纹理清晰,则判断根蒂的时候是在纹理清晰的范围内去判断。

四、决策树的目的
决策树的目的是产生一颗泛化能力强的决策树(个人理解就是产生一个通用的决策模型)
五、决策树如何选择最优划分属性

如上图所示(还是同一个图),可能大家会疑问,为什么我们的根节点是纹理,不是别的属性(根蒂,触感等属性表示不服),这就牵扯到最优划分属性这个概念。
最优划分属性:
顾名思义,用这个属性划分是最好的(到底什么最好呢),当然是节点纯度。在决策的时候还是希望节点包含的样本属于同一类(为了省时省力) 度量节点纯度的一个概念叫做“信息增益”
信息增益:
要想了解信息增益这个概念之前要先了解信息熵这个定义: 信息熵是用来表示样本集合纯度最常用的一种指标。(样本纯度就是字面意思,样本都是同一类就纯度高,信息熵的值就低)
信息熵的计算公式如下:

Pk 表示第K类样本在当前样本中所占的比例。y表示样本分类个数。
信息增益公式如下:

V表示属性a的几个可能值,比如触感有硬滑和软粘两种。Dv 则表的是在属性a的时候取得样本数。D表示所有样本个数。
信息增益例子:

图片数据来自西瓜书
从表可以看出好瓜占的比例是p1=8/17,坏瓜的比例 p2=9/17,可以计算出根节点的信息熵
![]()
然后计算各个属性的信息增益:本例先计算色泽:由表可知色泽有三个取值:青绿、乌黑、浅白,然后样本根据这三个值进行划分。

(同样是截自西瓜书,主要是公式不好打)
然后计算出“色泽”的信息增益

同理计算出其他属性的信息增益,最后比较得出纹理的最高。所以纹理首先对根节点进行划分。然后在划分之后,每个属性在根据新的样本进行划分。