数据挖掘实践（7）：基础理论（七）数学基础（七）概率（三）参数估计（一）

1、正态分布（⾼斯分布）

1.1 什么是正态分布

　　若随机变量X服从⼀个数学期望为μ、⽅差为σ^2的正态分布，记为N(μ，σ^2)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ = 0,σ = 1时的正态分布是标准正态分布。

　　期望：反映随机变量平均取值的⼤⼩。

　　　　设P(x) 是⼀个离散概率分布，⾃变量的取值范围为。其期望被定义为：
                                   

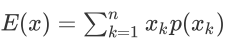
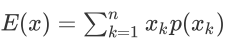
　　　　设P(x) 是⼀个连续概率密度函数，其期望为：

                              

　　　　⼤数定律规定，随着重复次数接近⽆穷⼤，数值的算术平均值⼏乎肯定地收敛于期望值。

　　⽅差：随机变量及其均值之间的偏离程度。

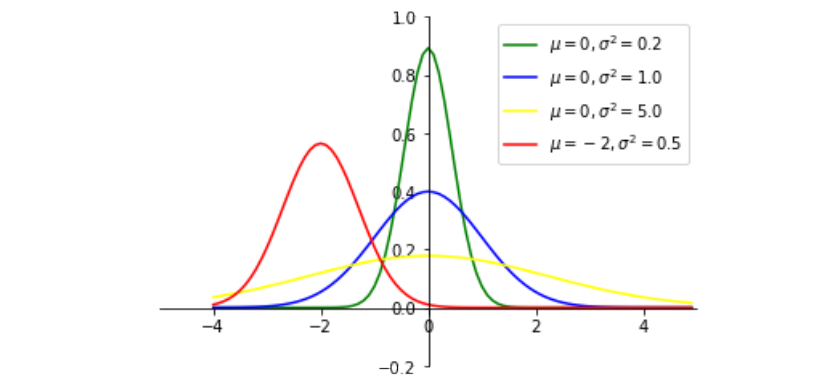
1.2 正态曲线

　　正态曲线呈钟型，两头低，中间⾼，左右对称因其曲线呈钟形，因此⼈们⼜经常称之为钟形曲线。

1.3 概率密度函数

                                         

import numpy as np
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
def demo1():
 mu ,sigma = 0, 1
 sampleNo = 1000000
 np.random.seed(0)
 s = np.random.normal(mu, sigma, sampleNo)
 plt.hist(s, bins=100, density=True)
 plt.show()
demo1()

import numpy as np
import matplotlib.mlab as mlab
import matplotlib.pyplot as plt
from scipy.stats import norm
def demo2():
 mu, sigma , num_bins = 0, 1, 50
 x = mu + sigma * np.random.randn(1000000)
 # 正态分布的数据
 n, bins, patches = plt.hist(x, num_bins, density=True, facecolor = 'blue',
alpha = 0.5)
 # 拟合曲线
 plt.plot(bins,(norm.pdf(bins, mu, sigma)))
 plt.xlabel('Expectation')
 plt.ylabel('Probability')
 plt.title('histogram of normal distribution: $mu = 0$, $sigma=1$')
 plt.subplots_adjust(left = 0.15)
 plt.show()
demo2()

#-*-coding:utf-8-*-
"""
python绘制标准正态分布曲线
"""
# ==============================================================
import numpy as np
import math
import matplotlib.pyplot as plt
def gd(x, mu=0, sigma=1):
 """根据公式，由⾃变量x计算因变量的值
 Argument:
 x: array
 输⼊数据（⾃变量）
 mu: float
 均值
 sigma: float
 ⽅差
 """
 left = 1 / (np.sqrt(2 * math.pi) * np.sqrt(sigma))
 right = np.exp(-(x - mu)**2 / (2 * sigma))
 return left * right
if __name__ == '__main__':
 # ⾃变量
 x = np.arange(-4, 5, 0.1)
 # 因变量（不同均值或⽅差）
 y_1 = gd(x, 0, 0.2)
 y_2 = gd(x, 0, 1.0)
 y_3 = gd(x, 0, 5.0)
 y_4 = gd(x, -2, 0.5)
 # 绘图
 plt.plot(x, y_1, color='green')
 plt.plot(x, y_2, color='blue')
 plt.plot(x, y_3, color='yellow')
 plt.plot(x, y_4, color='red')
 # 设置坐标系
 plt.xlim(-5.0, 5.0)
 plt.ylim(-0.2, 1)
 ax = plt.gca()
 ax.spines['right'].set_color('none')
 ax.spines['top'].set_color('none')
 ax.xaxis.set_ticks_position('bottom')
 ax.spines['bottom'].set_position(('data', 0))
 ax.yaxis.set_ticks_position('left')
 ax.spines['left'].set_position(('data', 0))
 plt.legend(labels=['$mu = 0, sigma^2=0.2$', '$mu = 0, sigma^2=1.0$',
'$mu = 0, sigma^2=5.0$', '$mu = -2, sigma^2=0.5$'])
 plt.show()

 

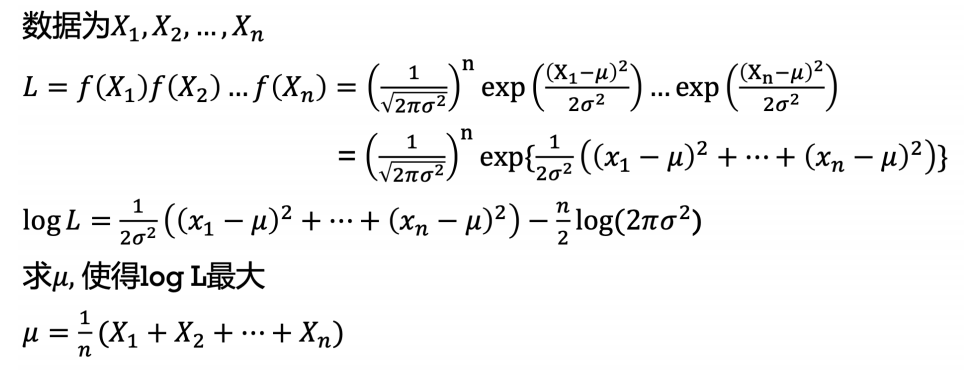
3、最⼤似然

3.1 似然函数

　　给定输出x时，关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ后变量X的概率：

　　　　　　　　L(θ|x)=P(X=x|θ)。

　　似然，就是可能性的意思。例如体重为20kg的哈⼠奇的可能性是多少，就称为体重为20kg的哈⼠奇的似然是多少。

3.2 极⼤似然估计

　　简单的说：极⼤似然估计就是利⽤已知的样本结果，反推最有可能（最⼤概率）导致这样结果的参 数值。 

根据科学，我们得到两个条件：

　　1.动物的体重是符合正态分布的。

　　2.我们“请”来了所有的⽹红哈⼠奇，得到了500只哈⼠奇的体重信息。

问：如何⽤这500只哈⼠奇去推测哈⼠奇的体重分布？

3.3 为什么要⽤极⼤似然估计

　　当我们使⽤机器学习解决具体现实问题时，我们是⽆法确切知道具体的数据分布情况的。例如我们现在想知道橘猫的体重分布，显然，我们是⽆法⼀只只去测的。这种情况在机器学习中⾮常普遍，那我们可不可以⽤部分已知数据去预测整体的分布呢？极⼤似然估计就是⼀个解决这类问题的⽅法。但是，这并不是绝对准确的，只能说实际情况最有可能接近这种猜测的分布。

3.4 使⽤极⼤似然估计⽅法的两个条件

　　1.我们假定数据服从某种已知的特定数据分布型。

　　2.我们已经得到了⼀定的数据集。

4、伯努利分布（两点分布）