随机森林在乳腺癌数据上的调参
在这节课中,我们了解了随机森林,并且学习了机器学习中调参的基本思想,了解了方差和偏差如何受到随机森林的参数们的影响。这一节,我们就来使用我们刚才学的,基于方差和偏差的调参方法,在乳腺癌数据上进行一次随机森林的调参。乳腺癌数据是sklearn自带的分类数据之一。
案例中,往往使用真实数据,为什么我们要使用sklearn自带的数据呢?因为真实数据在随机森林下的调参过程,往往非常缓慢。真实数据量大,维度高,在使用随机森林之前需要一系列的处理,因此不太适合用来做直播中的案例演示。在本章,我为大家准备了kaggle上下载的辨别手写数字的数据,有4W多条记录700多个左右的特征,随机森林在这个辨别手写数字的数据上有非常好的表现,其调参案例也是非常经典,但是由于数据的维度太高,太过复杂,运行一次完整的网格搜索需要四五个小时,因此不太可能拿来给大家进行演示。案例中用的泰坦尼克号数据,用来调参的话也是需要很长时间,因此我才选择sklearn当中自带的,结构相对清晰简单的数据来为大家做这个案例。
大家感兴趣的话,可以进群去下载数据,也可以直接到kaggle上进行下载,数据集名称是DigitRecognizer(https://www.kaggle.com/c/digit-recognizer)。
1. 导入需要的库
from sklearn.datasets import load_breast_cancer from sklearn.ensemble import RandomForestClassifier from sklearn.model_selection import GridSearchCV from sklearn.model_selection import cross_val_score import matplotlib.pyplot as plt import pandas as pd import numpy as np
2. 导入数据集,探索数据
data = load_breast_cancer() data data.data.shape data.target #可以看到,乳腺癌数据集有569条记录,30个特征,单看维度虽然不算太高,但是样本量非常少。过拟合的情况可能存 在。
3. 进行一次简单的建模,看看模型本身在数据集上的效果
rfc = RandomForestClassifier(n_estimators=100,random_state=90) score_pre = cross_val_score(rfc,data.data,data.target,cv=10).mean() score_pre #这里可以看到,随机森林在乳腺癌数据上的表现本就还不错,在现实数据集上,基本上不可能什么都不调就看到95%以 上的准确率
4. 随机森林调整的第一步:无论如何先来调n_estimators
""" 在这里我们选择学习曲线,可以使用网格搜索吗?可以,但是只有学习曲线,才能看见趋势 我个人的倾向是,要看见n_estimators在什么取值开始变得平稳,是否一直推动模型整体准确率的上升等信息 第一次的学习曲线,可以先用来帮助我们划定范围,我们取每十个数作为一个阶段,来观察n_estimators的变化如何 引起模型整体准确率的变化 """ #####【TIME WARNING: 30 seconds】##### scorel = [] for i in range(0,200,10): rfc = RandomForestClassifier(n_estimators=i+1, n_jobs=-1, random_state=90) score = cross_val_score(rfc,data.data,data.target,cv=10).mean() scorel.append(score) print(max(scorel),(scorel.index(max(scorel))*10)+1) plt.figure(figsize=[20,5]) plt.plot(range(1,201,10),scorel) plt.show() #list.index([object]) #返回这个object在列表list中的索引
5. 在确定好的范围内,进一步细化学习曲线
scorel = [] for i in range(35,45): rfc = RandomForestClassifier(n_estimators=i, n_jobs=-1, random_state=90) score = cross_val_score(rfc,data.data,data.target,cv=10).mean() scorel.append(score) print(max(scorel),([*range(35,45)][scorel.index(max(scorel))])) plt.figure(figsize=[20,5]) plt.plot(range(35,45),scorel) plt.show()
调整n_estimators的效果显著,模型的准确率立刻上升了0.005。接下来就进入网格搜索,我们将使用网格搜索对参数一个个进行调整。
为什么我们不同时调整多个参数呢?原因有两个:
1)同时调整多个参数会运行非常缓慢,在课堂上我们没有这么多的时间。
2)同时调整多个参数,会让我们无法理解参数的组合是怎么得来的,所以即便网格搜索调出来的结果不好,我们也不知道从哪里去改。在这里,为了使用复杂度-泛化误差方法(方差-偏差方法),我们对参数进行一个个地调整。
6. 为网格搜索做准备,书写网格搜索的参数
""" 有一些参数是没有参照的,很难说清一个范围,这种情况下我们使用学习曲线,看趋势 从曲线跑出的结果中选取一个更小的区间,再跑曲线 max_depth param_grid = {'n_estimators':np.arange(0, 200, 10)} param_grid = {'max_depth':np.arange(1, 20, 1)} param_grid = {'max_leaf_nodes':np.arange(25,50,1)} 对于大型数据集,可以尝试从1000来构建,先输入1000,每100个叶子一个区间,再逐渐缩小范围 有一些参数是可以找到一个范围的,或者说我们知道他们的取值和随着他们的取值,模型的整体准确率会如何变化,这 样的参数我们就可以直接跑网格搜索 param_grid = {'criterion':['gini', 'entropy']} param_grid = {'min_samples_split':np.arange(2, 2+20, 1)} param_grid = {'min_samples_leaf':np.arange(1, 1+10, 1)} param_grid = {'max_features':np.arange(5,30,1)}
7. 开始按照参数对模型整体准确率的影响程度进行调参,首先调整max_depth
#调整max_depth param_grid = {'max_depth':np.arange(1, 20, 1)} # 一般根据数据的大小来进行一个试探,乳腺癌数据很小,所以可以采用1~10,或者1~20这样的试探 # 但对于像digit recognition那样的大型数据来说,我们应该尝试30~50层深度(或许还不足够 # 更应该画出学习曲线,来观察深度对模型的影响 rfc = RandomForestClassifier(n_estimators=39 ,random_state=90 ) GS = GridSearchCV(rfc,param_grid,cv=10) GS.fit(data.data,data.target) GS.best_params_ GS.best_score_
在这里,我们注意到,将max_depth设置为有限之后,模型的准确率下降了。限制max_depth,是让模型变得简单,把模型向左推,而模型整体的准确率下降了,即整体的泛化误差上升了,这说明模型现在位于图像左边,即泛化误差最低点的左边(偏差为主导的一边)。
通常来说,随机森林应该在泛化误差最低点的右边,树模型应该倾向于过拟合,而不是拟合不足。
这和数据集本身有关,但也有可能是我们调整的n_estimators对于数据集来说太大,因此将模型拉到泛化误差最低点去了。然而,既然我们追求最低泛化误差,那我们就保留这个n_estimators,除非有其他的因素,可以帮助我们达到更高的准确率。
当模型位于图像左边时,我们需要的是增加模型复杂度(增加方差,减少偏差)的选项,因此max_depth应该尽量大,min_samples_leaf和min_samples_split都应该尽量小。
这几乎是在说明,除了max_features,我们没有任何参数可以调整了,因为max_depth,min_samples_leaf和min_samples_split是剪枝参数,是减小复杂度的参数。
在这里,我们可以预言,我们已经非常接近模型的上限,模型很可能没有办法再进步了。
那我们这就来调整一下max_features,看看模型如何变化。
8. 调整max_features
#调整max_features param_grid = {'max_features':np.arange(5,30,1)} """ max_features是唯一一个即能够将模型往左(低方差高偏差)推,也能够将模型往右(高方差低偏差)推的参数。我 们需要根据调参前,模型所在的位置(在泛化误差最低点的左边还是右边)来决定我们要将max_features往哪边调。 现在模型位于图像左侧,我们需要的是更高的复杂度,因此我们应该把max_features往更大的方向调整,可用的特征 越多,模型才会越复杂。max_features的默认最小值是sqrt(n_features),因此我们使用这个值作为调参范围的 最小值。 """ rfc = RandomForestClassifier(n_estimators=39 ,random_state=90 ) GS = GridSearchCV(rfc,param_grid,cv=10) GS.fit(data.data,data.target) GS.best_params_ GS.best_score_
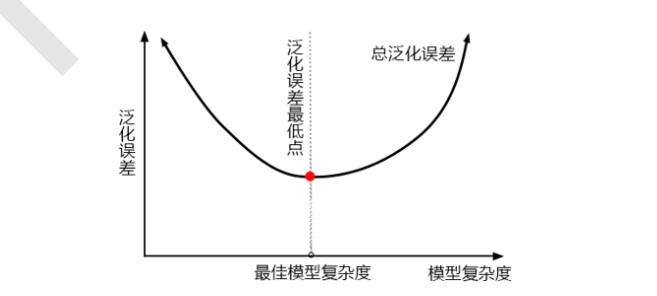
网格搜索返回了max_features的最小值,可见max_features升高之后,模型的准确率降低了。这说明,我们把模型往右推,模型的泛化误差增加了。前面用max_depth往左推,现在用max_features往右推,泛化误差都增加,这说明模型本身已经处于泛化误差最低点,已经达到了模型的预测上限,没有参数可以左右的部分了。
剩下的那些误差,是噪声决定的,已经没有方差和偏差的舞台了。
如果是现实案例,我们到这一步其实就可以停下了,因为复杂度和泛化误差的关系已经告诉我们,模型不能再进步了。调参和训练模型都需要很长的时间,明知道模型不能进步了还继续调整,不是一个有效率的做法。如果我们希望模型更进一步,我们会选择更换算法,或者更换做数据预处理的方式。
但是在课上,出于练习和探索的目的,我们继续调整我们的参数,让大家观察一下模型的变化,看看我们预测得是否正确。
依然按照参数对模型整体准确率的影响程度进行调参。
9. 调整min_samples_leaf
#调整min_samples_leaf param_grid={'min_samples_leaf':np.arange(1, 1+10, 1)} #对于min_samples_split和min_samples_leaf,一般是从他们的最小值开始向上增加10或20 #面对高维度高样本量数据,如果不放心,也可以直接+50,对于大型数据,可能需要200~300的范围 #如果调整的时候发现准确率无论如何都上不来,那可以放心大胆调一个很大的数据,大力限制模型的复杂度 rfc = RandomForestClassifier(n_estimators=39 ,random_state=90 ) GS = GridSearchCV(rfc,param_grid,cv=10) GS.fit(data.data,data.target) GS.best_params_ GS.best_score_
可以看见,网格搜索返回了min_samples_leaf的最小值,并且模型整体的准确率还降低了,这和max_depth的情况一致,参数把模型向左推,但是模型的泛化误差上升了。
在这种情况下,我们显然是不要把这个参数设置起来的,就让它默认就好了。
10. 不懈努力,继续尝试min_samples_split
#调整min_samples_split param_grid={'min_samples_split':np.arange(2, 2+20, 1)} rfc = RandomForestClassifier(n_estimators=39 ,random_state=90 ) GS = GridSearchCV(rfc,param_grid,cv=10) GS.fit(data.data,data.target) GS.best_params_ GS.best_score_
和min_samples_leaf一样的结果,返回最小值并且模型整体的准确率降低了。
11. 最后尝试一下criterion
#调整Criterion param_grid = {'criterion':['gini', 'entropy']} rfc = RandomForestClassifier(n_estimators=39 ,random_state=90 ) GS = GridSearchCV(rfc,param_grid,cv=10) GS.fit(data.data,data.target) GS.best_params_ GS.best_score_
12. 调整完毕,总结出模型的最佳参数
rfc = RandomForestClassifier(n_estimators=39,random_state=90) score = cross_val_score(rfc,data.data,data.target,cv=10).mean() score score - score_pre
在整个调参过程之中,我们首先调整了n_estimators(无论如何都请先走这一步),然后调整max_depth,通过max_depth产生的结果,来判断模型位于复杂度-泛化误差图像的哪一边,从而选择我们应该调整的参数和调参的方向。
如果感到困惑,也可以画很多学习曲线来观察参数会如何影响我们的准确率,选取学习曲线中单调的部分来放大研究(如同我们对n_estimators做的)。学习曲线的拐点也许就是我们一直在追求的,最佳复杂度对应的泛化误差最低点(也是方差和偏差的平衡点)。
网格搜索也可以一起调整多个参数,大家只要有时间,可以自己跑一下,看看网格搜索会给我们怎样的结果,有时候,它的结果比我们的好,有时候,我们手动调整的结果会比较好。
当然了,我们的乳腺癌数据集非常完美,所以只需要调n_estimators一个参数就达到了随机森林在这个数据集上表现得极限。在我们上周使用的泰坦尼克号案例的数据中,我们使用同样的方法调出了如下的参数组合。
rfc = RandomForestClassifier(n_estimators=68 ,random_state=90 ,criterion="gini" ,min_samples_split=8 ,min_samples_leaf=1 ,max_depth=12 ,max_features=2 ,max_leaf_nodes=36 )
基于泰坦尼克号数据调整出来的参数,数据的处理过程请参考上一期的完整视频。这个组合的准确率达到了83.915%,比单棵决策树提升了大约7%,比调参前的随机森林提升了2.02%,这对于调参来说其实是一个非常巨大的进步。
不过,泰坦尼克号数据的运行缓慢,大家量力量时间而行,可以试试看用复杂度-泛化误差方法(方差-偏差方法)来解读一下这个调参结果和过程。
