机器学习实战基础（三）：创建线性回归器

简介

回归是估计输入数据与连续值输出数据之间关系的过程。数据通常是实数形式的，我们的目标是估计满足输入到输出映射关系的基本函数。

准备工作

线性回归用输入变量的线性组合来估计基本函数。

线性回归的目标是提取输入变量与输出变量的关联线性模型，这就要求实际输出与线性方程预测的输出的残差平方和（sum of squares of differences）最小化。
这种方法被称为普通最小二乘法（Ordinary Least Squares，OLS）。

详细步骤

       假设你已经创建了数据文件data_singlevar.txt，文件里用逗号分隔符分割字段，第一个字段是输入值，第二个字段是与逗号前面的输入值相对应的输出值。你可以用这个文件作为输入参数。
（1）.创建一个Python文件regressor.py，然后在里面增加下面几行代码：

import sys 
import numpy as np  
filename = sys.argv[1] 
X = [] 
y = [] 
with open(filename, 'r') as f: 
    for line in f.readlines(): 
        xt, yt = [float(i) for i in line.split(',')]  
        X.append(xt) 
        y.append(yt) 

把输入数据加载到变量X和y，其中X是数据，y是标记。在代码的for循环体中，我们解析每行数据，用逗号分割字段。然后，把字段转化为浮点数，并分别保存到变量X和y中。

(2) 建立机器学习模型时，需要用一种方法来验证模型，检查模型是否达到一定的满意度（satisfactory level）。
为了实现这个方法，把数据分成两组：训练数据集（training dataset）与测试数据集（testing dataset）。
训练数据集用来建立模型，测试数据集用来验证模型对未知数据的学习效果。因此，先把数据分成训练数据集与测试数据集：

num_training = int(0.8 * len(X))  
num_test = len(X) - num_training 
 
# 训练数据 
X_train = np.array(X[:num_training]).reshape((num_training,1))  
y_train = np.array(y[:num_training]) 
 
# 测试数据 
X_test = np.array(X[num_training:]).reshape((num_test,1))  
y_test = np.array(y[num_training:]) 

这里用80%的数据作为训练数据集，其余20%的数据作为测试数据集。

(3) 现在已经准备好训练模型。接下来创建一个回归器对象，代码如下所示：

from sklearn import linear_model 
 
# 创建线性回归对象 
linear_regressor = linear_model.LinearRegression() 
 
# 用训练数据集训练模型 
linear_regressor.fit(X_train, y_train) 

(4) 我们利用训练数据集训练了线性回归器。向fit方法提供输入数据即可训练模型。用下面的代码看看它如何拟合：

import matplotlib.pyplot as plt 
 
y_train_pred = linear_regressor.predict(X_train)  
plt.figure() 
plt.scatter(X_train, y_train, color='green') 
plt.plot(X_train, y_train_pred, color='black', linewidth=4)  
plt.title('Training data') 
plt.show() 

(5) 在命令行工具中执行如下命令： 

$ python regressor.py data_singlevar.txt 

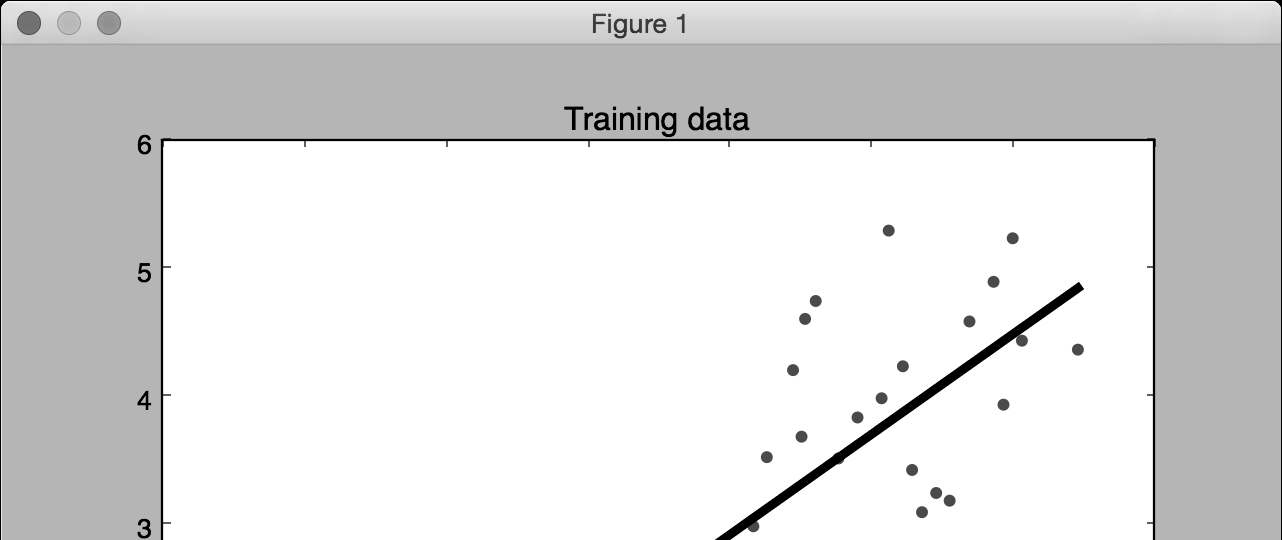
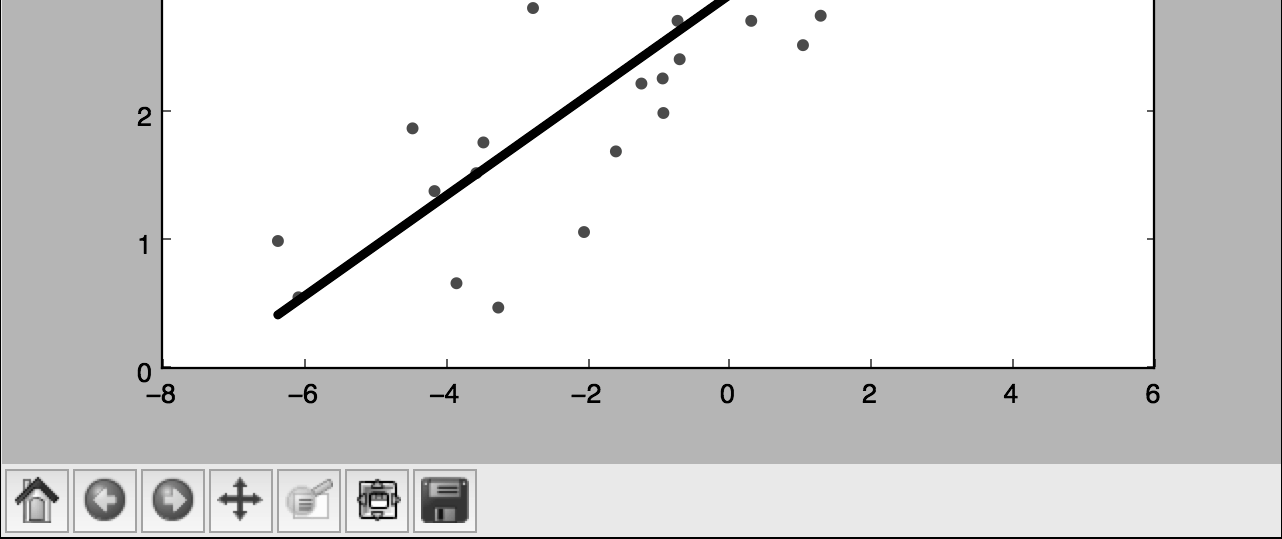
(6) 在前面的代码中，我们用训练的模型预测了训练数据的输出结果，但这并不能说明模型对未知的数据也适用，因为我们只是在训练数据上运行模型。
这只能体现模型对训练数据的拟合效果。从图1-2中可以看到，模型训练的效果很好。
(7) 接下来用模型对测试数据集进行预测，然后画出来看看，代码如下所示： 

y_test_pred = linear_regressor.predict(X_test) 
 
plt.scatter(X_test, y_test, color='green')  
plt.plot(X_test, y_test_pred, color='black', linewidth=4)  
plt.title('Test data') 
plt.show()