1 动态范围压缩介绍
自然界中真实场景能够表现比较广泛的颜色亮度区间,比如从很暗(10^-5 cd/m2)的黑夜到明亮(10^5 cd/m2)的太阳光,有将近10个数量级的动态方位。而传统显示设备所能显示的场景、视频和图像通常受限于硬件设备,通常只能表达出很小一部分的亮度范围,比如如常见的8比特图像显示0到255的整数范围,因此为了能够显示高动态范围的影响,需要实现从高动态范围图像(HDR)到低动态范围图像(LDR)的映射,并且不同显示设备的出现,需要实现HDR和之间的相互转换 ,即动态范围压缩(DRC,Dynamic Range Compression)。
动态范围压缩算法常见的分为全局映射和局部映射。全局映射:像素的一对一映射,降低一致的分辨率,这样得到的LDR图像的对比度大大地减少,容易丢失细节部分的信息
。局部映射:考虑像素和像素之间的关系,能够适当增强局部范围的亮度对比度,它保留了一定的细节,但是某些区域会出现失真的现象,并且它的复杂度较高
。鉴于这个原因,我们希望有一个理想算法:既要能保持像素的整体变化,又要能保存一部分细节特征,使得亮度效果能够达到人眼可以接受的接近现实的场景。
2 动态范围压缩算法
实现动态范围压缩有许多种算法,比如线性移位算法、对数映射算法、分段函数映射算法、自适应性对数映射算法、高动态范围图像可视化算法。
2.1 线性移位算法
原理:是最简单的DRC算法,它将以n比特整数表示的HDR图像直接右移(n—m)个比特得m(m<n)比特整数的LDR图像。
缺点:考虑像素颜色的分布,会使数值集中的颜色分辨率降低,对于大部分图像来说,像素颜色不均,并且多分布于中低数值区间,高数值区间的颜色较少,这样映射后的LDR图像,颜色暗的地方更暗了,丢失很多细节,颜色高亮的地方会变得很尖锐,有失真的表现。
2.2 对数映射算法
原理:为简便起见以2为底,将数值区间[0,2^n]对数化到区间[0,n],然后再线性变换到区间[0,2^m] 。
缺点:与线性移位算法一样,都是全局算法,不能对图像的局部进行有效的修正,图像效果一般,但是效率较高
。
2.3 分段函数映射
原理:考虑到低数值区间、高数值区间以及它们之间区域的不同特点,使用三段式的分段函数对HDR图像进行压缩,对不同的亮度区域进行分辨率调整。
优点:两端的线段斜率较小,中间的斜率较大,即算法有意地提高中间值像素的分辨率。映射曲线的两个拐点值视不同的图像而定,即它考虑到了图像的局部特征变化,
所以不完全是全局算法。
缺点:仍然是粗粒度的,因为它没有考虑像素之间的关系。
2.4 自适应性对数映射
原理:引入实际场景最高亮度值和现实场景最高亮度值的对数比,并且选取一个较优对比度调节算子,实现HDR到LDR的映射。
优点:样扩大中间亮度值的映射范围,压缩高亮度值的映射斜率。后两种算法的复杂度一般,图像效果比之前两种算法好。
2.5 高动态范围图像可视化算法
原理:用快速双向滤波器对输入图像进行对数域分解,分解为基本层和细节层,分别进行全局和局部映射算法,基本层进行直方图映射调整,细节层进行自适应细节增强。
优点:既保留了全局对比信息,又增强了局部细节,视觉效果更好一些,但是双向滤波器的引入,使得算法的复杂度较高。
本文为了考虑性能和实现复杂度,提出了一种新算法:以对数映射为基础,结合对数映射和分段映射的特点,划分出不同的亮度范围,然后分段映射。这样既不需要太高复杂度的算法将图像的全局信息和局部信息分开来,又能实现对局部区域的调节。
3 对数分段映射算法实现
对数分段映射算法的实现步骤如下:
(1) 将原始输入进行指定区间的改进对数映射
(2) 将对数区间进行分段调整
3.1 改进的对数映射
传统对数映射公式如下,其中:对数底数base和前面的系数a视具体的映射范围而定,这里取以2为底。
f(x) = a * logbase(x + 1)
改进全局映射步骤中的对数映射算法,以10比特的HDR图像为例,公式如下:
f(x) = [[lb(x+1) * 1..6]^2 - 0.5]; 0=<x<=1023
Matlab各自拟合的曲线对比如下(输入:[0,1023],输出:[0,255]):
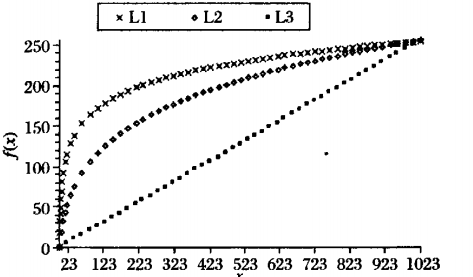
其中L1为传统对数算法,L2曲线为改进后的算法,L3为线性移位算法。可以看出改进后的L2曲线优势是扩 大了中间数值区域的映射范围,提高了该区域的分辨率。
3.2 对数区间进行分段调整
我们对局部区域进行适当处理,使得数据分布较多的区域能够扩大映射范围,数据分布较少的区域能够缩映
射范围,即将改进后的算法加以适应性调整后作用到不同的区间段上以产生更好的效果。
假如把需要映射的亮度区间分为两段:[0,511]和(511,1023],在这两段区间上使用不同的含参数的映射曲线:
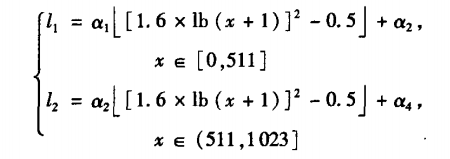
令A(x) = [(1.6 * lb(x + 1))^2 - 0.5],则满足如下条件:
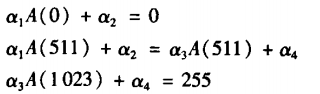
另外,引入一个渐变参数a: a = a3/a1 = N2/N1,其中Ni为亮度值分布在第i个区间内的像素个数,渐变系数值反映了每个区间像素分布的递增趋势。
4 算法仿真对比
以10bit的HDR图像为例,该图亮度值范围为0~1023,分为两个映射区间后的曲线表达式为:
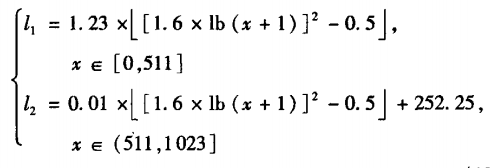
仿真对比如下:
线性移位算法 典型对数映射法 本文算法



结论:本文提出的算法更好地增强了高低亮度区域的对比度,并且高低亮度区域交界处变化平滑。