CF427 D. Palindromic characteristics 动态规划

835D - Palindromic characteristics

Observation I.

If the string is k-palindrome, then it is (k - 1)-palindrome.

Observation II.

The string is k-palindrome if and only if the both following conditions are true:

1. It is a palindrome.
2. It's left half is non-empty (k - 1)-palindrome.

Solution.

Let's calculate the following dp.

• dp[l][r] is the maximum k such that the substring built from characters from l to r is k-palindrome.
• The dynamics is calculated in the order of non-decreasing of substring lengths.
• The values for l = r and l = r - 1 are computed trivially.
• Let r - l > 1. Then, if s[l] ≠ s[r] or dp[l + 1][r - 1] = 0, dp[l][r] = 0. Otherwise dp[l][r] = dp[l][m] + 1, where .

When we have dp values, we can calculate cnt[k] — the number of substrings, which dp value is k. Then the number of substrings that are k-palindromes is .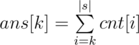

The solution works in O(|s|2) time and uses O(|s|2) memory.

Also, you could notice that the string can be no more than 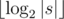-palindrome, and solve the problem in  time, reducing the memory usage to O(|s|).

C++ code: 29077222

Java code: 29077251

Python code: 29077276

#include <iostream> 
#include <string>
using namespace std;
const int N = 5005;
string s;
int n;
short dp[N][N];//dp[l][r] is the maximum k 
int ans[N];
int main()
{
    ios::sync_with_stdio(false);
    cin >> s;
    int n = (int)s.size();
    for (int len = 1; len <= n; ++len) {
        int l_r = n - len + 1;
        for (int l = 0; l < l_r; ++l) {
            int r = l + len;//dp[l][r], s[l,r)
            if (len == 1) { dp[l][r] = 1; continue; }
            if (len == 2) { dp[l][r] = (s[l] == s[r - 1] ? 2 : 0); continue; }
            if (s[l] != s[r - 1] || dp[l + 1][r - 1] == 0) continue;
            dp[l][r] = 1;
            int m = l + r >> 1;
            if (dp[l][m] && dp[m + (len&1)][r]) dp[l][r] = dp[l][m] + 1;
        }
    }
    for (int len = 1; len <= n; ++len) {
        int l_r = n - len + 1;
        for (int l = 0; l < l_r; ++l) {
            int r = l + len;
            ans[dp[l][r]]++;
        }
    }
    for (int i = n - 1; i >= 1; --i)
        ans[i] += ans[i + 1];
    cout << ans[1];
    for (int i = 2; i <= n; ++i)
        cout << " " << ans[i];
    cout << endl;

    return 0;
}

by wjsay 2017/8/1