前段时间刚看完c++语法部分的内容,现在开始着手研究下,用c++实现下一些基本的排序算法。![]() 因为是初学者的缘故,可能理解之处还是存在不到位之处,但权且当作学习过程中的一种心得体会,也算记录下自己学习的路程吧。(理解的浅陋之处望及时指出)
因为是初学者的缘故,可能理解之处还是存在不到位之处,但权且当作学习过程中的一种心得体会,也算记录下自己学习的路程吧。(理解的浅陋之处望及时指出)
所谓递归,就是方法自己调用自己,从而实现代码上的简化,同时也简化阅读人员的可读性。
递归的优势在于:当要求解一个问题时,在求解过程中,会碰到同样的处理过程。这个求解的过程就是递归的方法,不断递归的就是这个处理过程,而递归让这个问题逐渐变小,最终回到递归基上。
递归基:就是当问题足够简单时,或者已经不能再分解时,所能给出的返回结果,即为递归基。
这样说可能太抽象了,上例子了:![]()
比如:我们求解n!(n的阶乘),即1*2*3...n;
数学上: f(n) = n*f(n-1);(n>=2,n是自然数),这个式子有个好名叫递推公式
可以看出:f(n)和f(n-1)它们是同样的问题,所以处理过程一定是一样的,只是规模上的问题。
该问题的详细过程:![]()
当要求得f(n)时,我们要知道f(n-1),
求f(n-1)时,需求f(n-2)的值
...
最终要求f(1)的值,---------递归基的位置上
#include<iostream> int fun(int num); int main() { using namespace std; int num=5; cout << fun(num); return 0; } int fun(int num) { if(num==1) { return 1; } return num*fun(num-1); }
从上述代码可以看出,f(n)调用了f(n-1)的结果,同理f(n-1)会继续调用本身的方法,最终都会回归到递归基。
方法代码简化:![]()
int fun(int num) { return num==1?1:num*fun(num-1); }
从上面的例子,我们初步了解了递归的形式。下面会展示一道典型的递归用法。
常谈的斐波那契数列,又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、……
在数学上,斐波纳契数列以如下被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n>=2,n∈N*)
从递推公式中可以看出,它调用了自身,只是处理的规模变成了n-1和n-2;典型的递归式。
数列定义中可以看出递归基为:F(0)=0,F(1)=1;问题最终都会分解到递归基上。
上代码:
#include<iostream> int Fibonacci(int num); int main() { using namespace std; int num=5; cout << Fibonacci(num); return 0; } int Fibonacci(int num) { return num<=1?num:Fibonacci(num-1)+Fibonacci(num-2); }
程序还真是简单。
递归有个概略印象了,但程序并不是简洁就行了,还得运行起来快速。所以时间复杂度是必须考虑的,目前对空间复杂度方面暂时不考虑.
其运行图解如下图:
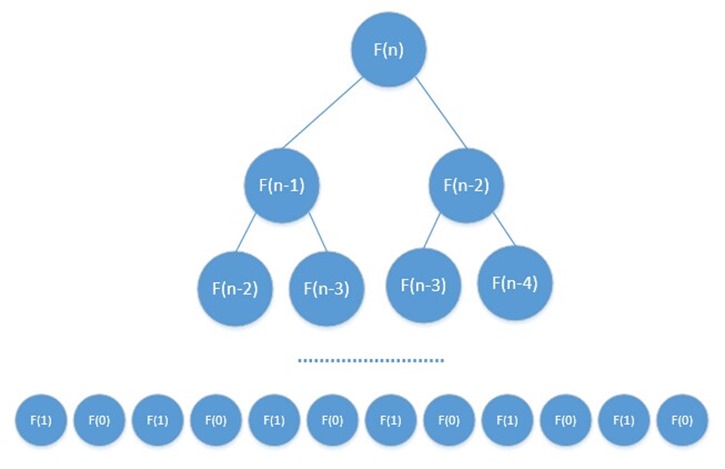
我们根据递推公式:T(n) = T(n-1)+T(n-2)
这是一个常系数的二阶线性齐次递推关系式,其求解方法就简单了:
得出其特征方程:
(黄金分割数的相反数哦。。。。。。)
从而得出复杂度如下:
呵呵,我们平时只记个O(2^n),其实它的时间复杂度是这样的,很奇怪吧。但确实如此,可见此算法不是个高效的算法,当n达到一定的值时,出结果的速度会长达很久很久,举个例子吧,若n取100吧,2GHz的处理器,1s钟能处理2g次,即2^31次,而1年相当于2^25次方,所以n取100时,需要 2^(100-25-31) 年,这得等多久啊。。。。。。。。。。
年,这得等多久啊。。。。。。。。。。
所以这不是一个合理的算法。。。。。。
分析上述高时间复杂度产生原因:有些已经计算过值,如F(5),在计算F(6)时,它会调用F(5),此时需重复计算F(5)的值,这样的多次的重复的计算,造就了如此高的时间复杂度。
若我们采取将这些计算过的值放在一个备忘表中,这样在下次调用中,直接从备忘表中取,我们可以瞬间降低时间开销。哈哈,是如此。
上述迭代是一种自上而下的算法,下面我们来看看自下而上的算法。
采用循环迭代的方法:
直接上代码:
#include<iostream> int Fibonacci(int num); int main() { using namespace std; int num=5; cout << Fibonacci(num); return 0; } int Fibonacci(int num) { int result=0; int sum=1; if(num<2) return num; int i=1; while(i<num) { sum += result; result = sum-result; i++; } return sum; }
图解:
从上可以看出,有时递归并不是一定是解决问题最好的办法,有时也许循环迭代倒是处理问题的好方法