此文摘自和整理大神博客,大神博客地址:https://www.cnblogs.com/f-ck-need-u/p/6089523.html
和https://www.cnblogs.com/clsn/p/8315833.html#auto-id-11。
1.互联网数据安全的介绍
1.互联网数据安全出现的背景
网络就是实现不同主机之间的通讯,网络出现之初利用TCP/IP协议簇的相关协议概念,已经满足了互连两台主机之间可以进行通汛的目的,虽然看似简简单单几句话,就描述了网络概念与网络出现的目的,但是为了真正实现两台主机之间的稳定可靠通讯,其实是一件非常困难的事情了,如果还要再通讯的基础上保证数据传输的安全性,可想而知,绝对是难上加难,因此,网络发明之初,并没有太关注TCP/IP互联协议中的安全问题。
对于默认的两台主机而言,早期传输数据信息并没有通过加密方式传输数据,设备两端传输的数据本身实际是明文的,只要能截取到传输的数据包,就可以直接看到传输的数据信息,所以根本没有安全性可言。
2.互联网数据安全涉及的问题
早期网络设备间进行通讯时,是采用明文逬行数据传输的,并没有网络安全技术可言。我们可以提出一种假设,如果在网络上的两台主机之间传输数据,就是采用明文的方式;并且对于网络传输而言,并没有相关的网络安全技术保驾护航,这样在互联网上进行数据传输,都有哪些网络风险需要进行面对。
Ø 网络安全问题--数据机密性
在网络传输数据信息时,对数据的加密是至关重要的,否则所有传输的数据都是可以随时被第三方看到,完全没有机密性可言。
Ø 网络安全问题--数据完整性
网络传输数据的完整性,也是安全领域中斋要考虑的里要环节,如果不能保证传输数据的完整性,那传输过程中的数据就有可能被任何人所篡改,而传输数琚双方又不能及早的进行发现,将会造成互连通汛双方所表达信息的意义完全不一致。因此,对于不芫整的数据信息,接收方应该进行相应判断,如果完整性验证错误,就拒绝接收相应的数据。
Ø 网络安全问题--身份验证问题
网络中传输数据时,很有可能传输的双方是第一次建立连接,进行相互通讯,既然是第一次见面沟通,如何确认对方的身份信悤,的确是我要进行通讯的对象呢?如果不是正确的通讯对象,在经过通讯后,岂不是将所有数据信息发送给了一个陌生人。
2.互联网数据安全的解决
1.加密算法的简介
为了解决互联网数据的安全问题,出现了以下安全加密算法
对称加密 :加密解密使用同一密钥,加解密速度快。随着人数增多,密钥数量急增n(n-1)/2。
非对称加密 :使用公私钥配对加解密,速度慢。公钥是从私钥中提取出来的,一般拿对方公钥加密来保证数据安全性,拿自己的私钥加密来证明数据来源的身份。
单向加密 :不算是加密,也常称为散列运算,用于生成独一无二的校验码(或称为指纹、特征码)来保证数据的完整性和一致性,如MD5、SHA。具有雪崩效应,任何一点数据的改变,生成的校验码值变化非常大。
2.数据机密性解决思路--利用对称加密算法和数据加密算法解决机密性
为了保证数据的机密性,首先可以采用的方法就是将数据通过相应数据加密算法,转换为其它的数据信息,然后再通过相应算法反推出真正的数据是什么。普通算法虽然已经解决了明文数据的机密性,可以在网络传输过程中不被直接看到明文数据。但是新的问题又产生了,既然明文数据是通过算法改变成了新的数据信息,如果第三方获得了算法,利用算法也是可以将密文数据信息,再次转换为明文数据信息,因此出现了对称加密算法,形象比喻来说:数据加密算法就好比是一本密码规则手册,而对称加密算法就是将手册放在了一个保险柜中进行了上锁传输,只有传递数据信息的双方知道打开保险柜的密码。
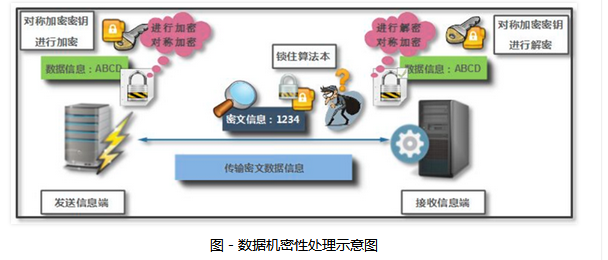
使用上述方法加密保证了数据的安全性,但是还未保证数据的完整性、一致性以及数据来源的可靠性。最主要的问题密钥有效管理的问题。
3.对称加密依赖算法diffie-hellman协议算法的介绍
上述为了解决数据机密性引入了对称加密算法的概率。对称加密算法依赖通讯双方需要进行数据密钥信息约定(密钥协商过程),在密钥相互可以获悉的过程中,需要借助密钥交换机制(Internet key exchange IKE),进而实现密钥的交互。为了满足网络中,两台主机间密钥交换统一的过程,需要引入一种新的协议diffie-hellman协议。
diffie-hellman协议算法实现的过程:
1) 首先发送方选取一个大素数P(只能被1和自己整除的数),再选取一个生产数g ,并且发送方将P与g经过互联网传输到接收方。
2) 数据传输的两端,发送方选取一个随机数x,接收方选取一个随机数y;发送方只知道随机数x ,接收方只知道随机数y , x和y不在互联网上进行传输。
3) 接收数据双方开始进行计算,对于发送方进行计算g的x次方对P取模的结果,传输给接收者;而接收方进行计算g的y次方对P取模的结果,传输给发送者。
4) 此时对于接收方获取到了发送方的g的x次方对P取模的结果,在取模结果的基础上进行y次方的运算,y就是接收方自身产生的随机数y;而对于发送方获取到了接收方的g的y次方对P取模的结果,在取模结果的基础上进行x次方的运算。x就是发送方自身产生的随机数x#此次,双方的加密运算密钥就实现了交换,并且是统一一致的,最终的密钥为g的xy次方对P取模的结果。
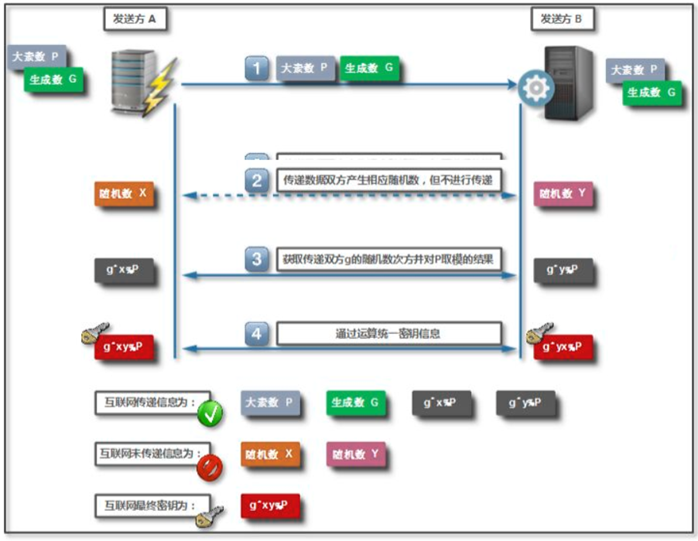
通过diffie-hellman协议算法最终可以实现了网络传输双方的密钥交换,并且通讯的双方也从此不用再对密钥进行管理记忆,只需要在进行传输数据前,逬行一次密钥的交换过程;即完成了对称密钥的生成过程。
并且如果网络中有攻击者在尝试破解出交换密钥时,就算通过比较复杂的数学运算,获悉了密钥,但也只是了解了上一次的数据交换密钥信息;下一次数据传输双方通讯时,还会交换新的密钥用于新的数据传输。
4.数据机密性和身份验证问题解决思路---数字签名
在保证了数据的安全性后,还需要保证数据的完整性、一致性以及数据来源的可靠性。
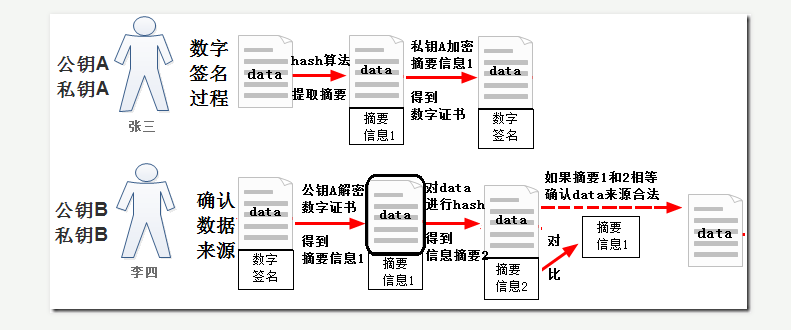
对于数据的完整性和一致性,使用单向加密算法,通过hash函数计算出数据独一无二的校验码,这个校验码称为“信息摘要(Message Digest)”。
对于数据来源可靠性,使用自己的私钥加密即可验证身份,因为获得数据后使用公钥不能解密的就证明数据不是配对私钥加密的。但是私钥加密速度慢,所以只用私钥加密摘要信息,加密后的摘要信息称为“数字签名(Signature)”。
用户获得数字签名后的数据,首先使用数据来源方的公钥解密,这样获得了数据和信息摘要部分,并确认了数据来源的可靠性。由于这时候数据部分是没有被加密的,所以用户也可以使用同种单向加密算法计算出摘要信息,然后对比来源方的摘要信息和自己计算出的摘要信息,如果相等则证明数据完全未被修改过,是完整一致的。
因此只要使用数字签名就能保证数据来源的可靠性、数据的完整性和一致性。
如图所示分别是数字签名和确认数据的全过程。