The 2020 ICPC Asia Taipei-Hsinchu Site Programming Contest-C题 Pyramid (思维,递推,规律)
题意:
一个n*n的矩阵,取其上三角矩阵,每个点的初值为L,左上角为起点,每次在起点放入一个球,如果当前点为L,则向下走,若为R,则向右走,则之后L会变成R,或R变成L。
问第k个球最后落入哪里。
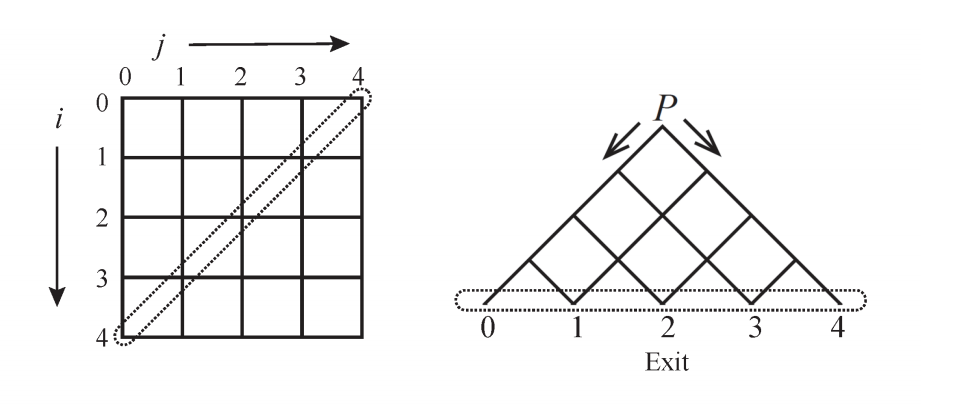
思路:
解题关键:
对于一个开关,若有x个小球经过此处,显然它会把 (lceilfrac{x}{2} ceil)个小球向左传送,会把(lfloorfrac{x}{2} floor)个小球向右传送。
由此我们可以自顶向下推出每一层的每个开关处有多少小球经过。
每一个开关会由其上方的1~2个开关转移过来,所以我们只需要开(dp[2][n])进行奇偶滚动数组dp求解。
如果我们知道了在一个小球到达某开关之前此处有多少小球经过,之前有奇数次经过该开关那么本次就向右走,之前有偶数次经过该开关那么本次就向左走,由此就能得到小球在这个开关的走向。
我们先求出前k-1个小球走过后每一个开关被走的次数,之后就能方便的求出第k个小球在每一层的走向,进而得到最后的结果。
代码:
#include <bits/stdc++.h>
using namespace std;
inline int readint() {int tmp = 0, fh = 1; char c = getchar(); while (c < '0' || c > '9') {if (c == '-') { fh = -1; } c = getchar();} while (c >= '0' && c <= '9') { tmp = tmp * 10 + c - 48, c = getchar(); } return tmp * fh;}
int n;
int val[2][10010];
int main()
{
int t;
t = readint();
while (t--) {
n = readint();
int k = readint();
if(n==1)
{
printf("0
");
continue;
}
val[0][0]=k-1;
int ans=0;
if(val[0][0]&1)
ans++;
for(int i=1;i<n-1;++i)
{
int last=0;
for(int j=0;j<i;++j)
{
val[i%2][j]=last+(val[(i-1)%2][j]+1)/2;
last=val[(i-1)%2][j]/2;
}
val[i%2][i]=last;
if(val[i%2][ans]&1)
{
ans++;
}
}
printf("%d
",ans);
}
return 0;
}