牛客练习赛26 E-树上路径 （树链剖分+线段树）

链接：https://ac.nowcoder.com/acm/contest/180/E
来源：牛客网

树上路径
时间限制：C/C++ 2秒，其他语言4秒
空间限制：C/C++ 262144K，其他语言524288K
64bit IO Format: %lld
题目描述
给出一个n个点的树，1号节点为根节点，每个点有一个权值
你需要支持以下操作
1.将以u为根的子树内节点(包括u)的权值加val
2.将(u, v)路径上的节点权值加val
3.询问(u, v)路径上节点的权值两两相乘的和

输入描述:
第一行两个整数n, m，表示树的节点个数以及操作个数

接下来一行n个数，表示每个节点的权值

接下来n - 1行，每行两个整数(u, v)，表示(u, v)之间有边

接下来m行
开始有一个数opt，表示操作类型
若opt = 1，接下来两个整数表示u, val
若opt = 2，接下来三个整数表示(u, v), val
若opt = 3，接下来两个整数表示(u, v)
含义均如题所示
输出描述:
对于每个第三种操作，输出一个数表示答案，对10^9+710
9
+7取模
示例1
输入
复制
3 8
5 3 1
1 2
1 3
3 1 2
3 1 3
3 2 3
1 1 2
2 1 3 2
3 1 2
3 1 3
3 2 3
输出
复制
15
5
23
45
45
115
说明
第一组询问结果：3 * 5 = 15
第二组询问结果：1 * 5 = 5
第三组询问结果：3 * 5 + 1 * 5 + 3 * 1 = 23
备注:
对于30 %30%的数据，n, m leqslant 100n,m⩽100
对于100 %100%的数据，n, m leqslant 10^5n,m⩽10
5

设a_ia
i
​
表示读入的第i个节点的权值以及每次修改的权值，保证a_i leqslant 10^4a
i
​
⩽10
4

保证不会有负数

思路：
很显然的树链剖分题，

前两个操作都是树链剖分的常规操作，

我们来看下第三个操作，我们假设询问的路径上有3个节点，权值分别是 a，b，c，，我们所求的结果就是ab+ac+b*c 来看下如何得到这个结果呢？

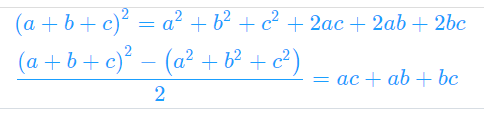
即我们可以维护区间的两个值（节点权值的sum和，和节点权值平方的sum）来得出区间的两两相乘再相加的结果（即操作3的输出）。

我们知道线段树维护区间sum和是很容易的，这里我就不讲了，那么如何维护权值平方的sum呢（即当区间中每一个值都加上t，如何方便得到新的平方sum和）？

我们假设一次更改的区间有三个节点，权值分别是a,b,c

这样我们可以看出，我们可以从线段树维护的两个值 ：sum和平方sum 来更新平方sum

例如区间加上t

新的平方sum= 更新前的平方sum+ 区间长度 乘 t 乘 t + 2t 乘 权值sum和。

这样就可以写本题了，记得pushdown的时候线段树的laze标记一定是+= 而不是 =

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {ll ans = 1; while (b) {if (b % 2)ans = ans * a % MOD; a = a * a % MOD; b /= 2;} return ans;}
inline void getInt(int* p);
const int maxn = 100010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
const ll mod=1e9+7ll;
std::vector<int> son[maxn];
ll w[maxn];
ll wt[maxn];
int id[maxn];
int SZ[maxn];
int wson[maxn];
int top[maxn];
int fa[maxn];
int n,m;
int dep[maxn];
int cnt;
void init()
{
    cnt=0;
}
void dfs1(int x,int pre,int step)
{
    fa[x]=pre;
    dep[x]=step;
    SZ[x]=1;
    int maxson=-1;
    for(auto & t:son[x])
    {
        if(t!=pre)
        {
            dfs1(t,x,step+1);
            SZ[x]+=SZ[t];
            if(SZ[t]>maxson)
            {
                maxson=SZ[t];
                wson[x]=t;
            }
        }
    }
}

void dfs2(int x,int topf)
{
    top[x]=topf;
    id[x]=++cnt;
    wt[cnt]=w[x];

    if(wson[x])
        dfs2(wson[x],topf);
    else
        return ;
    for(auto &t :son[x])
    {
        if(t==wson[x]||t==fa[x])
        {
            continue;
        }
        dfs2(t,t);
    }
}
struct node
{
    ll l,r;
    ll sum;
    ll csum;
    ll laze;
}segment_tree[maxn<<2];
void pushup(int rt)
{
    segment_tree[rt].sum=(segment_tree[rt<<1].sum+segment_tree[rt<<1|1].sum)%mod;
    segment_tree[rt].csum=(segment_tree[rt<<1].csum+segment_tree[rt<<1|1].csum)%mod;
}
void build(int rt,int l,int r)
{
    segment_tree[rt].l=l;
    segment_tree[rt].r=r;
    segment_tree[rt].laze=0ll;
    if(l==r)
    {
        segment_tree[rt].sum=wt[l];
        segment_tree[rt].csum=wt[l]*wt[l]%mod;
        return ;
    }
    int mid=(l+r)>>1;
    build(rt<<1,l,mid);
    build(rt<<1|1,mid+1,r);
    pushup(rt);
}
void pushdown(int rt)
{
    if(segment_tree[rt].laze)
    {
        ll val=segment_tree[rt].laze%mod;
        segment_tree[rt].laze=0ll;
        segment_tree[rt<<1].csum+=((segment_tree[rt<<1].r-segment_tree[rt<<1].l+1)*val%mod*val%mod+2ll*val%mod*(segment_tree[rt<<1].sum)%mod)%mod;
        segment_tree[rt<<1].csum%=mod;
        segment_tree[rt<<1].sum+=(segment_tree[rt<<1].r-segment_tree[rt<<1].l+1)*val%mod;
        segment_tree[rt<<1].sum%=mod;
        segment_tree[rt<<1].laze+=val;
        segment_tree[rt<<1].laze%=mod;
        segment_tree[rt<<1|1].csum+=((segment_tree[rt<<1|1].r-segment_tree[rt<<1|1].l+1)*val%mod*val%mod+2ll*val%mod*(segment_tree[rt<<1|1].sum)%mod)%mod;
        segment_tree[rt<<1|1].csum%=mod;
        segment_tree[rt<<1|1].sum+=(segment_tree[rt<<1|1].r-segment_tree[rt<<1|1].l+1)*val%mod;
        segment_tree[rt<<1|1].sum%=mod;
        segment_tree[rt<<1|1].laze+=val;
        segment_tree[rt<<1|1].laze%=mod;
    }
}

void update(int rt,int l,int r,ll val)
{
    val%=mod;
    if(segment_tree[rt].l>=l&&segment_tree[rt].r<=r)
    {
        segment_tree[rt].csum+=((segment_tree[rt].r-segment_tree[rt].l+1)*val%mod*val%mod+2ll*val%mod*segment_tree[rt].sum%mod)%mod;
        segment_tree[rt].csum%=mod;
        segment_tree[rt].laze+=val;
        segment_tree[rt].laze%=mod;
        segment_tree[rt].sum+=(segment_tree[rt].r-segment_tree[rt].l+1)*val%mod;
        segment_tree[rt].sum%=mod;
        return ;
    }
    pushdown(rt);
    int mid=segment_tree[rt].r+segment_tree[rt].l;
    mid>>=1;
    if(mid>=l)
    {
        update(rt<<1,l,r,val);
    }
    if(mid<r)
    {
        update(rt<<1|1,l,r,val);
    }
    pushup(rt);
}

void upson(int x,ll val)
{
    val%=mod;
    update(1,id[x],id[x]+SZ[x]-1,val);
}
void uprange(int x,int y,ll val)
{
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])
        {
            swap(x,y);
        }
        update(1,id[top[x]],id[x],val);
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])
    {
        swap(x,y);
    }
    update(1,id[x],id[y],val);
}
ll ask1(int rt,int l,int r)
{
    if(segment_tree[rt].l>=l&&segment_tree[rt].r<=r)
    {
        return segment_tree[rt].sum%mod;
    }
    pushdown(rt);
    int mid=(segment_tree[rt].l+segment_tree[rt].r)>>1;
    ll res=0ll;
    if(mid>=l)
    {
        res+=ask1(rt<<1,l,r);
        res%=mod;
    }
    if(mid<r)
    {
        res+=ask1(rt<<1|1,l,r);
        res%=mod;
    }
    return res;
}
ll ask2(int rt,int l,int r)
{
    if(segment_tree[rt].l>=l&&segment_tree[rt].r<=r)
    {
        return segment_tree[rt].csum%mod;
    }
    pushdown(rt);
    int mid=(segment_tree[rt].l+segment_tree[rt].r)>>1;
    ll res=0ll;
    if(mid>=l)
    {
        res+=ask2(rt<<1,l,r);
        res%=mod;
    }
    if(mid<r)
    {
        res+=ask2(rt<<1|1,l,r);
        res%=mod;
    }
    return res;
}

ll qrange(int x,int y)
{
    ll sum1=0ll;
    ll sum2=0ll;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]<dep[top[y]])
            swap(x,y);
        sum1=(sum1+ask1(1,id[top[x]],id[x]))%mod;
        sum2=(sum2+ask2(1,id[top[x]],id[x]))%mod;
        x=fa[top[x]];
    }
    if(dep[x]>dep[y])
    {
        swap(x,y);
    }
    sum1=(sum1+ask1(1,id[x],id[y]))%mod;
    sum2=(sum2+ask2(1,id[x],id[y]))%mod;
    ll res=(sum1*sum1%mod-sum2+mod)%mod;
    res=(res*powmod(2ll,mod-2ll,mod))%mod;
    return res;
}
int main()
{
    //freopen("D:\code\text\input.txt","r",stdin);
    //freopen("D:\code\text\output.txt","w",stdout);
    gbtb;
    cin>>n>>m;
    repd(i,1,n)
    {
        cin>>w[i];
    }
    int u,v;
    repd(i,2,n)
    {
        cin>>u>>v;
        son[u].pb(v);
        son[v].pb(u);
    }
    init();
    dfs1(1,-1,0);
    dfs2(1,1);
    build(1,1,n);
    int op;
    ll c;
    while(m--)
    {
        cin>>op;
        if(op==1)
        {
            cin>>u>>c;
            upson(u,c);
        }else if(op==2)
        {
            cin>>u>>v>>c;
            uprange(u,v,c);
        }else if(op==3)
        {
            cin>>u>>v;
            cout<<qrange(u,v)<<endl;
        }
    }
    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '
');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    }
    else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}