二叉树的遍历

1. 概念

树是连通的无环图，最常利用的有二叉树，即一个节点最多只有两个子节点，称为左子树和右子树。但是树都是相通的，无论是二叉树或者多个节点的树都能一般能用递归方法进行求解。二叉树节点之间的顺序一般不可调换，在数据结构定义时，左是左，右是右，不会说节点1，节点2。

二叉排序树又叫二叉查找树或者二叉搜索树：

1）若左子树不空，则左子树上所有结点的值均小于它的根节点的值；

2）若右子树不空，则右子树上所有结点的值均大于它的根结点的值；

3）左、右子树也分别为二叉排序树；4）没有键值相等的节点

2. 树的各种遍历

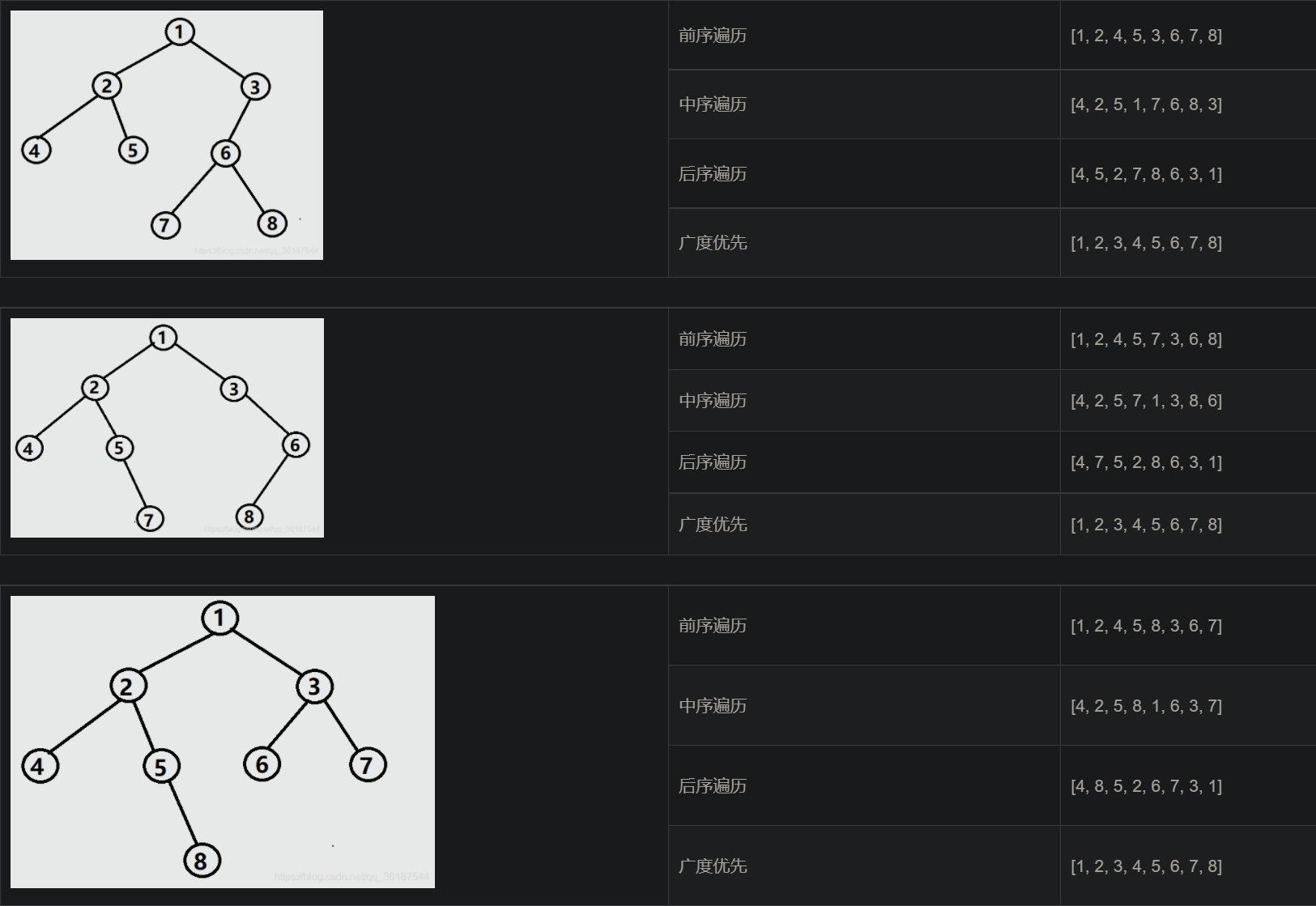
前序遍历，根-->左子树-->右子树

中序遍历，左子树-->根-->右子树

后序遍历，左子树-->右子树-->根

前序/后序+中序能够确定一个完整的树结构，因为前序/后序的根在第一位/最后一位，这样在中序中找到对应的根节点，以此递归，具体的题见leetCode105、106

广度优先遍历（Breadth FirstSearch，BFS,实际上就是逐层查找，又叫层次遍历，宽度优先搜索或横向优先搜索）

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

深度优先遍历（Depth First Search，DFS，主要有三种子方法，前中后序遍历）

前中后序遍历的递归写法

class Solution {
public:
    //前序遍历：
    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        traversal(root, result);
        return result;
    }
};
//中序遍历：
void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    vec.push_back(cur->val);    // 中
    traversal(cur->right, vec); // 右
}
//后序遍历：
void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    traversal(cur->right, vec); // 右
    vec.push_back(cur->val);    // 中
}