1 交换排序基本思想
交换排序的基本思想是:两两比较待排序记录的关键字,发现两个记录的次序相反时即进行交换,直到没有反序的记录为止。
应用交换排序基本思想的主要排序方法有:冒泡排序(Bubble sort)和快速排序(Quick sort)。
2 冒泡排序
2.1 冒泡排序思想
第一趟排序:首先将第一个记录的关键字和第二个记录的关键字比较,若为逆序,则将两个记录交换之,然后比较第二个和第三个的关键字。以此类推,直至第n-1个记录和第n个记录关键字比较为止。该过程为第一趟排序,使得最大的关键字排到了最后面。第二趟排序:对前n-1个记录进行相同操作,完成后使得次大的关键字排在n-1位置上。以此类推,进行第三、四次排序直到排序结束。判断排序结束条件是:在一趟排序过程中没有发生过交换记录的操作。一般第i趟排序是从第1个元素到(n-i+1)个记录依次比较相邻两个记录关键字,并在逆序时交换记录。
总结便是:共比较多少趟,每趟比较多少次。一个两重循环。
2.2 冒泡排序算法实现

public static void bubbleSort(int a[]) { int lenth = a.length; int temp; //共比较lenth-1趟 for (int i = 0; i < lenth - 1; i++) { //每轮比较length-1-j次 for (int j = 0; j < lenth - 1 - i; j++) { if (a[j] > a[j + 1]) { temp = a[j]; a[j] = a[j + 1]; a[j + 1] = temp; } } } }
2.3 算法效率分析
最好情况:初始序列为正序序列,只需进行一次排序,在此过程中进行n-1次比较,不移动数据。
最差情况:初始序列为逆序序列,需要进行n-1趟排序,需要进行内n(n-1)/2次比较,并且移动数据,每次比较都必须移动记录三次来达到交换记录位置。因此总的时间复杂度为O(n2)。
冒泡排序是就地排序,是稳定的。
3 快速排序
3.1 快速排序的思想
a:通过一趟排序将待排记录分割成独立两部分,其中一部分记录的关键字均比另一部分记录的关键小,则可以分别对这两部分记录继续进行排序,以达到这个序列有序。
b:设当前待排序的无序区为R[low..high], 在R[low..high]中任选一个记录作为基准(Pivot),以此基准将当前无序区划分为左、右两个较小的子区间R[low..pivotpos-1)和R[pivotpos+1..high],并使左边子区间中所有记录的关键字均小于等于基准记录(不妨记为pivot)的关键字pivot.key,右边的子区间中所有记录的关键字均大于等于pivot.key,而基准记录pivot则位于正确的位置(pivotpos)上,它无须参加后续的排序。通过递归调用快速排序对左、右子区间R[low..pivotpos-1]和R[pivotpos+1..high]快速排序。两个递归调用结束时,其左、右两个子区间已有序。
有点......,换个形象点的。
假设有数组 a={ 6, 1, 2, 7,9,3,4,5,8} ,要进行从小到大排序。考虑使用快速排序法。

总体思想:
第一步:以6为基准数,比6大的放在右边,比6小的放在左边。

第二步:将6左边的数以3为基准数,重复第一步。 将6右边的以9为基准数,重复第一步。
第一步具体操作:
1,将6给base,分别是i,j指向最左和最右。
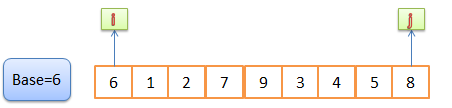
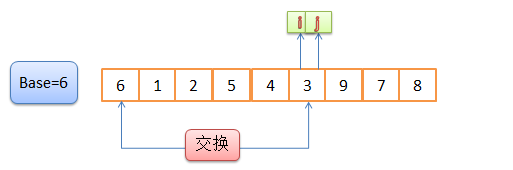
2,对j从右往左找比6小的数,对i从左往右找比i大的数。找到交换。

3,继续重复2的操作

4,直到i=j,交换base与i指向的值。
3.2 快速排序算法实现

public static void QuickSort(int a[], int left, int right) { if (left > right) return; int base = a[left]; int i = left; int j = right; while (i != j) { while (a[j] >= base && j > i) { j--; } while (a[i] <= base && j > i) { i++; } if (i < j) { int t = a[i]; a[i] = a[j]; a[j] = t; } } a[left] = a[i]; a[i] = base; QuickSort(a, left, i - 1); QuickSort(a, i + 1, right); }
3.3 算法分析
3.3.1 最坏时间复杂度:
最坏情况是每次划分选取的基准都是当前无序区中关键字最小(或最大)的记录,划分的结果是基准左边的子区间为空(或右边的子区间为空),而划分所得的另一个非空的子区间中记录数目,仅仅比划分前的无序区中记录个数减少一个。
因此,快速排序必须做n-1次划分,第i次划分开始时区间长度为n-i+1,所需的比较次数为n-i(1≤i≤n-1),故总的比较次数达到最大值:n(n-1)/2=O(n2)。
如果按上面给出的划分算法,每次取当前无序区的第1个记录为基准,那么当文件的记录已按递增序(或递减序)排列时,每次划分所取的基准就是当前无序区中关键字最小(或最大)的记录,则快速排序所需的比较次数反而最多。
3.3.2 最好时间复杂度
在最好情况下,每次划分所取的基准都是当前无序区的"中值"记录,划分的结果是基准的左、右两个无序子区间的长度大致相等。总的关键字比较次数:0(nlgn)
因为快速排序的记录移动次数不大于比较的次数,所以快速排序的最坏时间复杂度应为0(n2),最好时间复杂度为O(nlgn)。
3.3.3 平均时间复杂度
尽管快速排序的最坏时间为O(n2),但就平均性能而言,它是基于关键字比较的内部排序算法中速度最快者,快速排序亦因此而得名。它的平均时间复杂度为O(nlgn)。
3.3.4 空间复杂度
快速排序在系统内部需要一个栈来实现递归。若每次划分较为均匀,则其递归树的高度为O(lgn),故递归后需栈空间为O(lgn)。最坏情况下,递归树的高度为O(n),所需的栈空间为O(n)。
3.3.5 快速排序是非稳定的。
4 测试代码

package com.Sort; public class Sort { public static void main(String[] args) { // TODO Auto-generated method stub int a[] = { 6, 1, 2, 7,9,3,4,5,8 }; printSort(a); // bubbleSort(a); QuickSort(a, 0, a.length - 1); printSort(a); } /** * * @param a: */ public static void bubbleSort(int a[]) { int lenth = a.length; int temp; //共比较lenth-1趟 for (int i = 0; i < lenth - 1; i++) { //每轮比较length-1-j次 for (int j = 0; j < lenth - 1 - i; j++) { if (a[j] > a[j + 1]) { temp = a[j]; a[j] = a[j + 1]; a[j + 1] = temp; } } } } public static void QuickSort(int a[], int left, int right) { if (left > right) return; int base = a[left]; int i = left; int j = right; while (i != j) { while (a[j] >= base && j > i) { j--; } while (a[i] <= base && j > i) { i++; } if (i < j) { int t = a[i]; a[i] = a[j]; a[j] = t; } } a[left] = a[i]; a[i] = base; QuickSort(a, left, i - 1); QuickSort(a, i + 1, right); } public static void printSort(int a[]) { for (int i = 0; i < a.length; i++) { System.out.print(a[i] + " "); } System.out.println(); } }
