树状数组的一些基本操作。
树状数组支持单点修改和查询区间和的操作,但和线段树不同,它不支持区间修改操作(有些题目可以将区间修改转化为单点修改,有些则不可以)。下面介绍树状数组的预处理和基本操作。
1.求lowbit(n)
上一篇博客介绍了lowbit的定义和使用定义的基本求法。但是依据定义求lowbit未免麻烦。因而,求lowbit需要导入公式:lowbit(n)=n&(-n)。
求lowbit函数:
int lowbit(int n){//求n的lowbit
return n&(-n);
}
2.对某个元素进行加法操作
根据树状数组的性质,对于任意一个结点x,只有结点c[x]及其祖先结点保存的区间和中含a[x],所以我们只需要对x不断向上搜索即可。
代码:
void update(int x,int y){//将x位置元素加上y
for(;x<=N;x+=lowbit(x){//依次寻找x的父节点
c[x]+=y;//进行更新
}
}
这里在寻找x的父节点时运用了上一篇博客中的性质③(具体的证明方法我也不会qwq)。
举例证明:
假设我们要对A[2]进行加x的操作。
2的lowbit值为2,则第一步2变成了4,对C[4]进行处理。4的lowbit值为4,则第二步变成了8,对C[8]进行处理。此时已到达循环边界。
再假设我们要对A[5]进行加x的操作。
5的lowbit值为1,则第一步5变成了6,对C[6]进行处理。6的lowbit值为2,则第二步变成了8,对C[8]进行处理。此时已到达循环边界。
3.查询前缀和操作
前缀和的求法:求出x的二进制表示中每个等于1的位,把[1,x]分成logN个小区间,而每个小区间的区间和已保存在数组c中。
代码(我也不会证):
int sum(int x){//求1~x的区间和
int ans=0;
for(;x;x-=lowbit(x);){
ans+=c[x];
}
return ans;
}
举例证明: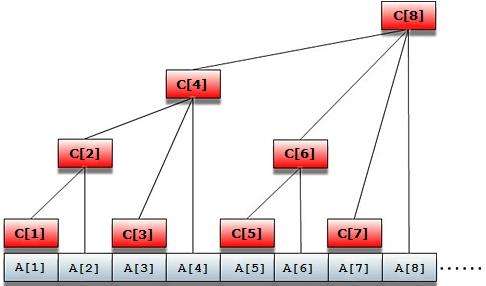
假设我们要求A[6]的前缀和。
首先我们设答案为ans,将ans+=C[6],则此时ans已包含A[5~6]的值。
接下来,因为6的lowbit值为2,所以x变为4,将ans+=C[4],则此时ans已包含A[1~6]的值。
最后,因为4的lowbit值为4,所以x变为0,到达循环边界,退出循环。
4.统计A[X]~A[Y]的值
调用上面的sum函数,则A[X]~A[Y]=sum(y)-sum(x-1)。
以上是树状数组支持的4个基本操作。