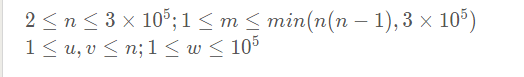$SCOJ4427 Miss Zhao's Graph$

(problem)

给定一个包含n个顶点m条边的带权有向图，找一条边数最多的路径，且路径上的边的权值严格递增。
图中可能有重边和自环。

(题意非常简单:n个点 m个带权边 最多能连成多少条边)

(看起来像搜索 就拿搜索水了一波)
(然后吧评测都卡爆了（而且只有9pts）)
总是觉得好亏
(打了一只前向星+DFS瞎搜)（大雾）

(~~恶心的DP题~~)
(9pts -> 0pts -> 64pts -> 73pts - >91pts ->100pts)

数据范围很大 显然(O(N)) (or) $O(M) $
这题用搜索可以达到 (O(N*玄学)) 玄学 = 一次搜索时间 >(如果带上记忆化 应该快点)
(那么DP的解法是O(M)的 每条边跑一次 记录一次)
重点 ->“递增”
首先 要按权值给边排序
(所以 应该注重权值相同的边)
(if(i < m and edge[i].dis == edge[i+1].dis) continue ;)
(加不加等于都没有关系 因为初始值是0)
(权值相同就直接跳过 否则会Wrong Answer)
(这是特判权值相同的边)
cnt数组用来储存边权相同的情况
这句(cnt[edge[k].to] = max ( cnt[edge[k].to] , dp[edge[k].from] + 1 ) ;) 不要手欠把dp和cnt打错 否则喜提WA数量不等(滑稽
还有一句话 (十年OI一场空 不开LL见祖宗orz)
实测int WA了一个点

---

(code)

#include <bits/stdc++.h>
using namespace std;
typedef long long LL ;
inline LL In() { LL res(0),f(1); register char c = getchar() ;
	while(!isdigit(c)) { if(c == '-') f = -1 ; c = getchar() ; }
	while(isdigit(c)) res = (res << 1) + (res << 3) + (c & 15) , c = getchar() ; return res * f ;
}
int n , m ;
const int N = 300000 ;
struct node{
    int from ;
    int to ;
    int dis ;
}edge[N] ;
LL cnt[N] ;
LL dp[N] ;
bool cmp(node x,node y) { return x.dis < y.dis ; }
signed main() {
	memset(edge,0,sizeof(edge)) ; memset(dp,0,sizeof(dp)) ;
    n = In() ; m = In() ;
    for(register int i =1 ; i <= m ; i ++) {//读入
    	int u = In() , v = In() , w = In() ;
		edge[i] = (node){u,v,w} ;
    }
    sort(edge+1 , edge+m+1 , cmp) ;//排序
	int pos = 1 ;
	for(register int i = 1 ;i <= m ;i ++) {//DP
        if(i < m and edge[i].dis == edge[i+1].dis) continue ;//特判权值相同
        for(register int k = pos ; k <= i ; k ++) cnt[edge[k].to] = max ( cnt[edge[k].to] , dp[edge[k].from] + 1 ) ;
		for(register int k = pos ; k <= i ; k ++) dp[edge[k].to] = cnt[edge[k].to] ;
        pos = i + 1 ;
    }
	cout << * max_element( dp + 1 , dp + n + 1 ) << endl ;//最大值函数
    return 0;
}