NetworkX 使用（二）

• 官方教程
• 博客：NetworkX

%pylab inline

import networkx as nx

Populating the interactive namespace from numpy and matplotlib

# 创建一个空图
G = nx.Graph()

节点

G.add_node(1)  # 添加一个节点
G.node

NodeView((1,))

G.add_nodes_from([2, 3])  # 添加多个节点
G.node

NodeView((1, 2, 3))

H 是一个有 (10) 个节点的链状图，即有 (n) 个节点 (n-1) 条边的连通图：

H = nx.path_graph(10)
nx.draw(H)
plt.show()

# 从 nbunch 中添加节点
G.add_nodes_from(H) # 或者 G.add_nodes_from(H.nodes()) 

G1 = nx.Graph()

G1.add_node(H)  # 将 H 当作节点

nx.draw(G1)  # 仅仅只有一个节点

现在图 G1 就包含了一个节点 H, 即该节点是一个图。可以看到这种灵活性是非常强大的，它允许图的图，文件的图，函数的图等等。因此我们应该好好思考如何构建我们的应用程序才能使我们的节点是有用的实体。当然我们可以在图中使用一个唯一的标识符或者使用一个不同的字典的键来标识节点信息。（如果该 hash 依赖于它的内容，则我们不应该改变节点对象）

nx.draw(G)

边

G = nx.Graph()
G.add_edge(1, 2)   # 添加一条边
nx.draw(G)

等价于

e = (2, 3)
G.add_edge(*e)
nx.draw(G)

添加多条边

G.add_edges_from([(2, 4), (2, 1)])
nx.draw(G)

我们新添加节点和边时，NetworkX 会自动忽略掉已经存在的边和节点的添加：

G.add_edges_from(H.edges())   # 通过 ebunch 添加边
nx.draw(G)

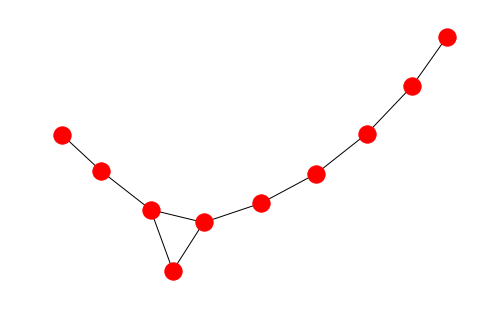
我们可以用下列的方法拆除图：
G.remove_node(), G.remove_nodes_from(), G.remove_edge(), G.remove_edges_from()

G.remove_node(4)
nx.draw(G)

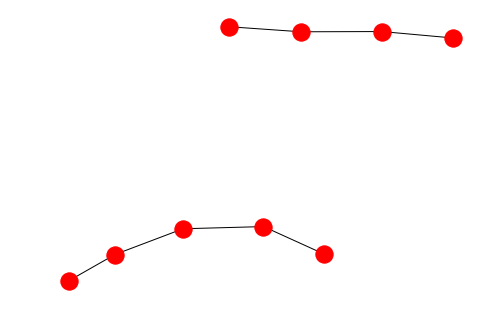
G.add_node("spam")       # 添加节点"spam"
nx.draw(G)

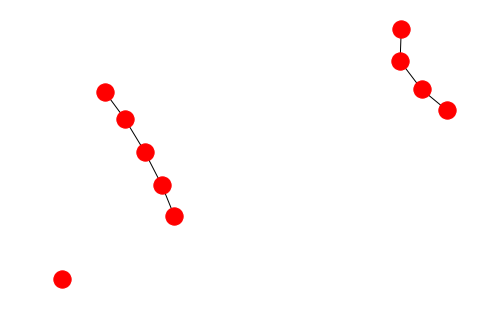
G.add_nodes_from("spam") # 添加节点's' 'p' 'a' 'm'
nx.draw(G)

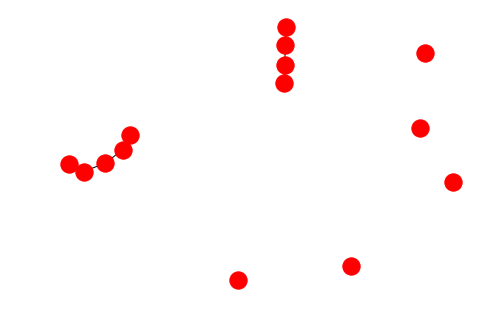
我们可以通过如下函数查看图的属性：

print('节点数', G.number_of_nodes())

print('边数', G.number_of_edges())

节点数 14
边数 7

print('节点列表', G.nodes())
print('边列表', G.edges())
print('节点 2 的邻居节点列表', list(G.neighbors(2)))

节点列表 [1, 2, 3, 0, 5, 6, 7, 8, 9, 'spam', 's', 'p', 'a', 'm']
边列表 [(1, 2), (1, 0), (2, 3), (5, 6), (6, 7), (7, 8), (8, 9)]
节点 2 的邻居节点列表 [1, 3]

下面的内容参考 What to use as nodes and edges

节点和边的使用

在 NetworkX 中节点和边并没有被指定一个对象，因此你就可以自由地指定节点和边的对象。最常见的对象是数值和字符串，但是一个节点可以是任意 hash对象（除了 None 对象），一条边也可以关联任意的对象x，比如：
G.add_edge(a,b,object=x)：
举个关于边关联对象的例子，假如a 和 b 是两个人，而他们两个人之间的联系（边），可以是一个概率，即边的对象是一个概率值，表示这两个人之间每天通电话的可能性。

可以看到这是十分强大而且有用的，但是如果你滥用该方法将会导致意想不到的后果，除非你对 Python 真的很熟悉。如果你不是很确定，你可以考虑使用 conver_node_label_to_integers()，他可以将一个图的所有节点按顺序转化为整数对象赋给另一个图。

访问边

下面的是老版本的说法：

除了上面的提到的那些访问节点和边的方法以外（ eg: Graph.nodes(), Graph.edges(), Graph.neighbors() …），当你只是想想要遍历它们时，迭代的版本 (eg: Graph.edges_iter()) 可以省去返回它们时创建如此很大的一个表去存储它们。

实际上，新版的 NetworkX 已经将它们默认封装为了迭代器。

快速直接的访问图的数据结构可以通过下表来实现。
（注意：不要去改变返回的字典，因为它是图数据结构中的一部分，直接的操作可能导致图处于一个不一致的状态。）

G = nx.Graph()
G.add_edge(1, 2, length = 10)
G.add_edge(1, 3, weight =  20)
G.add_edge(2, 3, capacity = 15)
nx.draw(G)

print(G[1])  # Warning: do not change the resulting dict

{2: {'length': 10}, 3: {'weight': 20}}

print(G[1][12])

{'length': 10}

You can safely set the attributes of an edge using subscript notation if the edge already exists.

G.add_edge(1,4)
G[1][13]['color']='blue'

Fast examination of all edges is achieved using adjacency iterators. Note that for undirected graphs this actually looks at each edge twice.

add_weight_edges_from 函数的作用是通过一个 ebunch 添加一些节点和边，边默认其属性为 ”weight”)
说明：其实 adjacency() 返回的是一个所有节点的二元组 (node, adjacency dict) 的迭代器

FG = nx.Graph()
FG.add_weighted_edges_from([(1,2,0.125),(1,3,0.75),(2,4,1.2),(3,4,0.375)])
nx.draw(FG)

for n, nbrs in FG.adjacency():
    for nbr, eattr in nbrs.items():
        data = eattr['weight']
        if data < 0.5: 
            print('(%d, %d, %.3f)' % (n, nbr, data))

(1, 2, 0.125)
(2, 1, 0.125)
(3, 4, 0.375)
(4, 3, 0.375)

Convenient access to all edges is achieved with the edges method.

for (u,v,d) in FG.edges(data='weight'):
    if d<0.5: print('(%d, %d, %.3f)'%(u,v,d))

(1, 2, 0.125)
(3, 4, 0.375)