深层神经网络

import tensorflow as tf
from numpy.random import RandomState

常用函数与运算

tf.clip_by_value函数将张量限定在一定的范围内：

sess = tf.InteractiveSession()

v = tf.constant([[1., 2., 3.], [4., 5., 6.]])
tf.clip_by_value(v, 2.5, 4.5).eval()  # 小于2.5的数值设为2.5，大于4.5的数值设为4.5

array([[ 2.5,  2.5,  3. ],
       [ 4. ,  4.5,  4.5]], dtype=float32)

tf.log 对张量所有元素进行对数运算

tf.log(v).eval()

array([[ 0.        ,  0.69314718,  1.09861231],
       [ 1.38629436,  1.60943794,  1.79175949]], dtype=float32)

v1 = tf.constant([[1., 2.], [3., 4.]])
v2 = tf.constant([[5., 6.], [7., 8.]])   
(v1 * v2).eval()          # 对应元素相乘

array([[  5.,  12.],
       [ 21.,  32.]], dtype=float32)

tf.matmul(v1, v2).eval()  # 矩阵乘法

array([[ 19.,  22.],
       [ 43.,  50.]], dtype=float32)

tf.reduce_mean(v).eval()

3.5

tf.reduce_mean(input_tensor, axis=None, keep_dims=False, name=None, reduction_indices=None)

Computes the mean of elements across dimensions of a tensor.

x = tf.constant([[1., 1.], [2., 2.]])
print(tf.reduce_mean(x).eval())
print(tf.reduce_mean(x, 0).eval())  
print(tf.reduce_mean(x, 1).eval()) 

1.5
[ 1.5  1.5]
[ 1.  2.]

tf.reduce_mean(tf.square(v1 - v2)).eval()

16.0

自定义损失函数

[Loss(y, y^{'}) = sum_{i =1}^{n} f(y_i, y^{'}_i) ]

$$
    f(x,y) = 
    egin{cases}
    a(x - y) & x > y \
    b(y - x) & x leq y
    end{cases}
$$

v1 = tf.constant([1., 2., 3., 4.])
v2 = tf.constant([4., 3., 2., 1.])
f = tf.greater(v1, v2)
f.eval()

array([False, False,  True,  True], dtype=bool)

tf.where(f, v1, v2).eval()

array([ 4.,  3.,  3.,  4.], dtype=float32)

1. 定义神经网络的相关参数和变量。

batch_size = 8
# 两个输入节点
x = tf.placeholder(tf.float32, shape=(None, 2), name="x-input")
# 回归问题一般只有一个输出节点
y_ = tf.placeholder(tf.float32, shape=(None, 1), name='y-input')
w1= tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))
y = tf.matmul(x, w1)

2. 设置自定义的损失函数。

# 定义损失函数使得预测少了的损失大，于是模型应该偏向多的方向预测。
loss_less = 10
loss_more = 1
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * loss_more, (y_ - y) * loss_less))
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)

3. 生成模拟数据集。

rdm = RandomState(1)
X = rdm.rand(128,2)
# 加入不可预测的噪音(均值为0 的小量)，以此观察不同的损失函数对预测结果的影响
Y = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]

4. 训练模型。

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 5000
    for i in range(STEPS):
        start = (i*batch_size) % 128
        end = (i*batch_size) % 128 + batch_size
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 1000 == 0:
            print("After %d training step(s), w1 is: " % (i))
            print(sess.run(w1), "
")
    print("Final w1 is: 
", sess.run(w1))

After 0 training step(s), w1 is: 
[[-0.81031823]
 [ 1.4855988 ]] 

After 1000 training step(s), w1 is: 
[[ 0.01247112]
 [ 2.1385448 ]] 

After 2000 training step(s), w1 is: 
[[ 0.45567414]
 [ 2.17060661]] 

After 3000 training step(s), w1 is: 
[[ 0.69968724]
 [ 1.8465308 ]] 

After 4000 training step(s), w1 is: 
[[ 0.89886665]
 [ 1.29736018]] 

Final w1 is: 
 [[ 1.01934695]
 [ 1.04280889]]

5. 重新定义损失函数，使得预测多了的损失大，于是模型应该偏向少的方向预测。

loss_less = 1
loss_more = 10
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_) * loss_more, (y_ - y) * loss_less))
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 5000
    for i in range(STEPS):
        start = (i*batch_size) % 128
        end = (i*batch_size) % 128 + batch_size
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 1000 == 0:
            print("After %d training step(s), w1 is: " % (i))
            print(sess.run(w1), "
")
    print("Final w1 is: 
", sess.run(w1))

After 0 training step(s), w1 is: 
[[-0.81231821]
 [ 1.48359871]] 

After 1000 training step(s), w1 is: 
[[ 0.18643527]
 [ 1.07393336]] 

After 2000 training step(s), w1 is: 
[[ 0.95444274]
 [ 0.98088616]] 

After 3000 training step(s), w1 is: 
[[ 0.95574027]
 [ 0.9806633 ]] 

After 4000 training step(s), w1 is: 
[[ 0.95466018]
 [ 0.98135227]] 

Final w1 is: 
 [[ 0.95525807]
 [ 0.9813394 ]]

6. 定义损失函数为MSE。

loss = tf.losses.mean_squared_error(y, y_)
train_step = tf.train.AdamOptimizer(0.001).minimize(loss)

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    STEPS = 5000
    for i in range(STEPS):
        start = (i*batch_size) % 128
        end = (i*batch_size) % 128 + batch_size
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 1000 == 0:
            print("After %d training step(s), w1 is: " % (i))
            print(sess.run(w1), "
")
    print("Final w1 is: 
", sess.run(w1))

After 0 training step(s), w1 is: 
[[-0.81031823]
 [ 1.4855988 ]] 

After 1000 training step(s), w1 is: 
[[-0.13337609]
 [ 1.81309223]] 

After 2000 training step(s), w1 is: 
[[ 0.32190299]
 [ 1.52463484]] 

After 3000 training step(s), w1 is: 
[[ 0.67850214]
 [ 1.25297272]] 

After 4000 training step(s), w1 is: 
[[ 0.89473999]
 [ 1.08598232]] 

Final w1 is: 
 [[ 0.97437561]
 [ 1.0243336 ]]

神经网络优化算法

• 反向传播算法(backpropagation): 在所有参数上使用梯度下降算法，是训练神经网络的核心算法
• 梯度下降算法(gradient decent): 优化单个参数的取值

记 ( heta) 为神经网络的参数，(J( heta)) 表示给定的参数取值下，训练数据集上损失函数的大小，因而神经网络的优化过程可以转化为寻找使得(J( heta)) 最小的 ( heta) 的过程。

使用梯度下降法，迭代更新参数 ( heta) ，不断沿着梯度反方向让参数朝着总损失更小的方向更新。

对于( heta) 梯度为(frac{partial J( heta)}{partial heta})

定义学习率 (eta) 为每次参数更新的幅度。

[ heta_{n+1} = heta_n - eta frac{partial J( heta_n)}{partial heta_n} ]

学习率的设置

假设我们要最小化函数 (y=x^2), 选择初始点 (x_0=5)

1. 学习率为1的时候，x在5和-5之间震荡。

import tensorflow as tf
TRAINING_STEPS = 10
LEARNING_RATE = 1
x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)

train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(TRAINING_STEPS):
        sess.run(train_op)
        x_value = sess.run(x)
        print("After %s iteration(s): x%s is %f."% (i+1, i+1, x_value))

After 1 iteration(s): x1 is -5.000000.
After 2 iteration(s): x2 is 5.000000.
After 3 iteration(s): x3 is -5.000000.
After 4 iteration(s): x4 is 5.000000.
After 5 iteration(s): x5 is -5.000000.
After 6 iteration(s): x6 is 5.000000.
After 7 iteration(s): x7 is -5.000000.
After 8 iteration(s): x8 is 5.000000.
After 9 iteration(s): x9 is -5.000000.
After 10 iteration(s): x10 is 5.000000.

2. 学习率为0.001的时候，下降速度过慢，在901轮时才收敛到0.823355。

TRAINING_STEPS = 1000
LEARNING_RATE = 0.001
x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)

train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(TRAINING_STEPS):
        sess.run(train_op)
        if i % 100 == 0: 
            x_value = sess.run(x)
            print("After %s iteration(s): x%s is %f."% (i+1, i+1, x_value))

After 1 iteration(s): x1 is 4.990000.
After 101 iteration(s): x101 is 4.084646.
After 201 iteration(s): x201 is 3.343555.
After 301 iteration(s): x301 is 2.736923.
After 401 iteration(s): x401 is 2.240355.
After 501 iteration(s): x501 is 1.833880.
After 601 iteration(s): x601 is 1.501153.
After 701 iteration(s): x701 is 1.228794.
After 801 iteration(s): x801 is 1.005850.
After 901 iteration(s): x901 is 0.823355.

3. 使用指数衰减的学习率，在迭代初期得到较高的下降速度，可以在较小的训练轮数下取得不错的收敛程度。

tf.train.exponential_decay函数指数衰减学习率。

tf.train.exponential_decay(learning_rate, global_step, decay_steps, decay_rate, staircase=False, name=None)

• learning_rate ：事先设定的初始学习率
• decay_steps: 衰减速度，staircase = True时代表了完整的使用一遍训练数据所需要的迭代轮数(= 总训练样本数/每个batch中的训练样本数)
• decay_rate: 衰减系数
• staircase: 默认为False，此时学习率随迭代轮数的变化是连续的(指数函数)；为 True 时，global_step/decay_steps 会转化为整数，此时学习率便是阶梯函数(staircase function)

TRAINING_STEPS = 100
global_step = tf.Variable(0)
LEARNING_RATE = tf.train.exponential_decay(0.1, global_step, 1, 0.96, staircase=True)

x = tf.Variable(tf.constant(5, dtype=tf.float32), name="x")
y = tf.square(x)
train_op = tf.train.GradientDescentOptimizer(LEARNING_RATE).minimize(y, global_step=global_step)

with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for i in range(TRAINING_STEPS):
        sess.run(train_op)
        if i % 10 == 0:
            LEARNING_RATE_value = sess.run(LEARNING_RATE)
            x_value = sess.run(x)
            print("After %s iteration(s): x%s is %f, learning rate is %f."% (i+1, i+1, x_value, LEARNING_RATE_value))

After 1 iteration(s): x1 is 4.000000, learning rate is 0.096000.
After 11 iteration(s): x11 is 0.690561, learning rate is 0.063824.
After 21 iteration(s): x21 is 0.222583, learning rate is 0.042432.
After 31 iteration(s): x31 is 0.106405, learning rate is 0.028210.
After 41 iteration(s): x41 is 0.065548, learning rate is 0.018755.
After 51 iteration(s): x51 is 0.047625, learning rate is 0.012469.
After 61 iteration(s): x61 is 0.038558, learning rate is 0.008290.
After 71 iteration(s): x71 is 0.033523, learning rate is 0.005511.
After 81 iteration(s): x81 is 0.030553, learning rate is 0.003664.
After 91 iteration(s): x91 is 0.028727, learning rate is 0.002436.

正则化

w = tf.constant([[1., -2.], [-3, 4]])
with tf.Session() as sess:
    print(sess.run(tf.contrib.layers.l1_regularizer(.5)(w)))  # 0.5 为权重
    print(sess.run(tf.contrib.layers.l2_regularizer(.5)(w)))

5.0
7.5

1. 生成模拟数据集。

import tensorflow as tf
import matplotlib.pyplot as plt
import numpy as np

data = []
label = []
np.random.seed(0)

# 以原点为圆心，半径为1的圆把散点划分成红蓝两部分，并加入随机噪音。
for i in range(150):
    x1 = np.random.uniform(-1,1)
    x2 = np.random.uniform(0,2)
    if x1**2 + x2**2 <= 1:
        data.append([np.random.normal(x1, 0.1),np.random.normal(x2,0.1)])
        label.append(0)
    else:
        data.append([np.random.normal(x1, 0.1), np.random.normal(x2, 0.1)])
        label.append(1)
        
data = np.hstack(data).reshape(-1,2)
label = np.hstack(label)
plt.scatter(data[:,0], data[:,1], c=label,
           cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.show()

2. 定义一个获取权重，并自动加入正则项到损失的函数。

由于集合(collection)可以在计算图 (tf.Graph) 中保存一组实体(比如张量)，故它可以计算带 L2 正则化的损失函数的方法。

tf.add_to_collection 函数将这个新生成变量的 L2 正则化损失项加入集合，此函数的第一个参数是集合的名字，第二个参数是要加入这个集合的内容。

# 获取一层神经网络边上的权重，并将这个权重的 L2 正则化损失加入名称为 'losses' 的集合中
def get_weight(shape, lambda1):
    # 生成一个变量
    var = tf.Variable(tf.random_normal(shape), dtype = tf.float32) 
    tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(lambda1)(var))
    # 返回生成的变量
    return var

3. 定义神经网络。

x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))
sample_size = len(data)

# 每层节点的个数
layer_dimension = [2,10,5,3,1]
# 神经网络的层数
n_layers = len(layer_dimension)

# 这个变量维护前向传播时最深层的节点，开始的时候就是输入层
cur_layer = x
# 当前层的节点数
in_dimension = layer_dimension[0]

# 循环生成网络结构
for i in range(1, n_layers):
    # layer_dimension[i]为下一层的节点个数
    out_dimension = layer_dimension[i]
    # 生成当前层中权重的变量，并将这个变量的 L2 正则化损失加入计算图上的集合
    weight = get_weight([in_dimension, out_dimension], 0.003)
    bias = tf.Variable(tf.constant(0.1, shape=[out_dimension]))
    # 使用eLU激活函数
    cur_layer = tf.nn.elu(tf.matmul(cur_layer, weight) + bias)
    # 进入下层之前的节点个数更新为当前层节点个数
    in_dimension = layer_dimension[i]

y = cur_layer

# 在定义神经网络前向传播的同时已经将所有的L2正则化损失加入了图上的集合，
# 这里只需要计算刻画模型在训练数据上表现的损失函数
mse_loss = tf.reduce_sum(tf.pow(y_ - y, 2)) / sample_size
# mse_loss = tf.reduce_mean(tf.square(y_ - y))

# 将均方误差损失函数加入损失集合
tf.add_to_collection('losses', mse_loss)
# tf.get_collection 返回一个列表(所有这个集合中的元素)
# 在这个样例中，这些元素就是损失函数的不同部分，将它们加起来就可以得到最终的损失函数
loss = tf.add_n(tf.get_collection('losses'))

4. 训练不带正则项的损失函数mse_loss。

过拟合：当一个模型过为复杂之后，它可以很好地“记忆”每个训练数据中随机噪音的部分而忘记去“学习”训练数据的通用趋势。

# 定义训练的目标函数mse_loss，训练次数及训练模型
train_op = tf.train.AdamOptimizer(0.001).minimize(mse_loss)
TRAINING_STEPS = 40000

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for i in range(TRAINING_STEPS):
        sess.run(train_op, feed_dict={x: data, y_: label})
        if i % 2000 == 0:
            print("After %d steps, mse_loss: %f" % (i,sess.run(mse_loss, feed_dict={x: data, y_: label})))

    # 画出训练后的分割曲线       
    xx, yy = np.mgrid[-1.2:1.2:.01, -0.2:2.2:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x:grid})
    probs = probs.reshape(xx.shape)

plt.scatter(data[:,0], data[:,1], c=label,
           cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()

After 0 steps, mse_loss: 1.619369
After 2000 steps, mse_loss: 0.042168
After 4000 steps, mse_loss: 0.026728
After 6000 steps, mse_loss: 0.022706
After 8000 steps, mse_loss: 0.016363
After 10000 steps, mse_loss: 0.007347
After 12000 steps, mse_loss: 0.006512
After 14000 steps, mse_loss: 0.001360
After 16000 steps, mse_loss: 0.000292
After 18000 steps, mse_loss: 0.000142
After 20000 steps, mse_loss: 0.000084
After 22000 steps, mse_loss: 0.000056
After 24000 steps, mse_loss: 0.000041
After 26000 steps, mse_loss: 0.000036
After 28000 steps, mse_loss: 0.000030
After 30000 steps, mse_loss: 0.000025
After 32000 steps, mse_loss: 0.000023
After 34000 steps, mse_loss: 0.000021
After 36000 steps, mse_loss: 0.000019
After 38000 steps, mse_loss: 0.000018

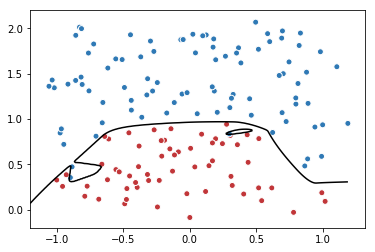
5. 训练带正则项的损失函数loss。

为了避免过拟合问题，一个非常常用的方法是正则化(regularization)。

正则化：在损失函数中加入刻画模型复杂程度的指标。即对于损失函数 (J( heta)) ,需要优化的是 (J( heta) + lambda R(w))。

• (R(w)): 刻画模型复杂程度的指标
• (lambda): 表示模型复杂损失在总损失中的比例
• ( heta): 包括权重 (w) 和偏置项 (b)

L1正则化

使得参数变得更稀疏(即有更多的参数变为0，这样可以达到类似特征选择的功能)

[R(w) = ||w||_1 ]

tf.contrib.layers.l1_regularizer()

L2正则化

[R(w) = ||w||_2^2 ]

tf.contrib.layers.l2_regularizer()

L1-L2正则化

[R(w) = alpha||w||_1 + (1 - alpha)||w||_2^2 ]

# 定义训练的目标函数loss，训练次数及训练模型
train_op = tf.train.AdamOptimizer(0.001).minimize(loss)
TRAINING_STEPS = 40000

with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for i in range(TRAINING_STEPS):
        sess.run(train_op, feed_dict={x: data, y_: label})
        if i % 2000 == 0:
            print("After %d steps, loss: %f" % (i, sess.run(loss, feed_dict={x: data, y_: label})))

    # 画出训练后的分割曲线       
    xx, yy = np.mgrid[-1:1:.01, 0:2:.01]
    grid = np.c_[xx.ravel(), yy.ravel()]
    probs = sess.run(y, feed_dict={x:grid})
    probs = probs.reshape(xx.shape)

plt.scatter(data[:,0], data[:,1], c=label,
           cmap="RdBu", vmin=-.2, vmax=1.2, edgecolor="white")
plt.contour(xx, yy, probs, levels=[.5], cmap="Greys", vmin=0, vmax=.1)
plt.show()

After 0 steps, loss: 1.591393
After 2000 steps, loss: 0.100526
After 4000 steps, loss: 0.066279
After 6000 steps, loss: 0.057447
After 8000 steps, loss: 0.055713
After 10000 steps, loss: 0.055156
After 12000 steps, loss: 0.055092
After 14000 steps, loss: 0.055040
After 16000 steps, loss: 0.054985
After 18000 steps, loss: 0.054964
After 20000 steps, loss: 0.054956
After 22000 steps, loss: 0.054953
After 24000 steps, loss: 0.054952
After 26000 steps, loss: 0.054951
After 28000 steps, loss: 0.054951
After 30000 steps, loss: 0.054951
After 32000 steps, loss: 0.054951
After 34000 steps, loss: 0.054950
After 36000 steps, loss: 0.054950
After 38000 steps, loss: 0.054950

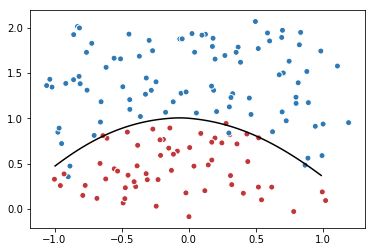
滑动平均模型

滑动平均模型会将每一轮迭代得到的模型综合起来，从而使得最终得到的模型在测试数据上更加健壮(robust)。

tf.train.ExponentialMovingAverage 需要提供一个衰减率(decay)来控制模型更新的速度。

ExponentialMovingAverage 对每一个变量会维护一个影子变量(shadow variable)，这个影子变量的初始值就是相应变量的初始值，而每次运行变量更新时，影子变量的值会更新为：

[ ext{shadow_variable} = ext{decay} imes ext{shadow_variable} + (1 - ext{decay}) * ext{variable} ]

• shadow_variable 为影子变量，
• variable 为待更新变量
• decay 为衰减率，它越大模型越趋于稳定，在实际应用中decay一般会设置为接近 1 的数。

还可以使用 num_updates参数来动态设置decay的大小：

[ ext{decay} = minegin{Bmatrix} ext{decay}, frac{1 + ext{num_updates}}{10 + ext{num_updates}}end{Bmatrix} ]

1. 定义变量及滑动平均类

# 定义一个变量用来计算滑动平均，且其初始值为0，类型必须为实数
v1 = tf.Variable(0, dtype=tf.float32)
# step变量模拟神经网络中迭代的轮数，可用于动态控制衰减率
step = tf.Variable(0, trainable=False)

# 定义一个滑动平均的类(class)。初始化时给定了衰减率为0.99和控制衰减率的变量step
ema = tf.train.ExponentialMovingAverage(0.99, step)
# 定义一个更新变量滑动平均的操作。这里需要给定一个列表，每次执行这个操作时，此列表中的变量都会被更新。
maintain_averages_op = ema.apply([v1]) 

2. 查看不同迭代中变量取值的变化。

with tf.Session() as sess:
    
    # 初始化
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    # 通过ema.average(v1)获取滑动平均后的变量取值。在初始化之后变量v1的值和v1 的滑动平均均为0
    print(sess.run([v1, ema.average(v1)]))
    
    # 更新变量v1的取值
    sess.run(tf.assign(v1, 5))
    sess.run(maintain_averages_op)
    print(sess.run([v1, ema.average(v1)])) 
    
    # 更新step和v1的取值
    sess.run(tf.assign(step, 10000))  
    sess.run(tf.assign(v1, 10))
    sess.run(maintain_averages_op)
    print(sess.run([v1, ema.average(v1)]))       
    
    # 更新一次v1的滑动平均值
    sess.run(maintain_averages_op)
    print(sess.run([v1, ema.average(v1)]))       

[0.0, 0.0]
[5.0, 4.5]
[10.0, 4.5549998]
[10.0, 4.6094499]