今天lyq大佬问了菜鸡我一道最短路的题,结果把我问懵逼了,WC ,最短路忘干净了,咕咕咕,吓得我赶紧去看了看最短路,顺便水一篇博客
floyed
这东西是个区间dp,找了中间点来更新区间的最优值
没什么好说的就是(3)层循环跑,也没什么用
适用范围:无负权回路即可,边权可正可负,运行一次算法即可求得任意两点间最短路
时间复杂度:O((n^3))这复杂度除非CCF用神威太湖之光给你跑,否则就会TLE
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#include<stack>
#include<queue>
using/nnamespace/nstd;
int/na[101][3];
double/nf[101][101];
int/nn,i,j,k,x,y,m,s,e;
int/nmain()
{
cin>>n;
for(int/ni=1;i<=n;++i)
cin>>a[i][1]>>a[i][2];
cin>>m;
memset(f,0x7fffffff,sizeof(f));
for(int/ni=1;i<=m;++i)
{
cin>>x>>y;
f[x][y]=f[y][x]=sqrt((pow(double(a[x][1]-a[y][1]),2))+(pow(double(a[x][2]-a[y][2]),2)));
}
cin>>s>>e;
for(int/nk=1;k<=n;++k)
for(int/ni=1;i<=n;++i)
for(int/nj=1;j<=n;++j)
if((i!=j)&&(i!=k)&&(k!=j)&&(f[i][k]+f[k][j]<f[i][j]))
f[i][j]=f[i][k]+f[k][j];
cout<<f[s][e];
return/n0;
}
优化:
利用对称性,只适用于无向图
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<queue>
#include<stack>
#include<iomanip>
#include<cctype>
using namespace std;
const int maxn=2501;
long long int map[maxn][maxn];
int main() {
int n,m,s,t;
cin>>n>>m>>s>>t;
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
map[i][j]=0x7fffff;
for(int i=1; i<=m; i++) {
int x,y,z;
cin>>x>>y>>z;
map[x][y]=z;
map[y][x]=z;
}
for(int k=1; k<=n; k++)
for(int i=1; i<=n; i++)
for(int j=1; j<=i; j++)//根据对称性优化
map[j][i]=map[i][j]=min(map[i][j],map[i][k]+map[k][j]);
printf("%lld ",map[s][t]);
return 0;
}
Dijkstra
-
适用范围:无负权回路,边权必须非负,单源最短路
-
时间复杂度:优化前O((n^2))
数组dis[u]表示u到s点的最短距离。
我们一直找点u = min{ dis[k] , k点未访问 },这个点就是最短路上的点,然后根据其他点v跟u点的关系去更新下dis[v],不断重复找和更新即可。
dis[s]=0将源点加入最短路,然后循环n-1次每次找出一个最短路上的点,找的方法是直接找出剩下的点中dis[ ]最小的那个点u,u点就是最短路上的点,然后看看其他点v到s点的距离会不会因为
这个u点的加入而改变,即若dis[v] > dis[u] + distance[u][v] 则更新dis[v]为 dis[u] + distance[u][v]。
#include<iostream>
#include<cstdio>
#include<cmath>
#include<queue>
#include<stack>
using namespace std;
const int maxn=1e9;
const int hhh=105;
int inq[hhh],n,m,s,x,y,z,a[105][105];
int dis[hhh];
int main() {
cin>>n>>m>>s;//别忘了 !!!!!!!!!!!!!!!!!!!
for(int i=1; i<=m; ++i) {//别忘了 !!!!!!!!!!!!!!!!!!!
for(int j=1; j<=m; ++j) {//别忘了 !!!!!!!!!!!!!!!!!!!
if(i==j) {//别忘了 !!!!!!!!!!!!!!!!!!!
a[i][j]=0;//别忘了 !!!!!!!!!!!!!!!!!!!
} else {//别忘了 !!!!!!!!!!!!!!!!!!!
a[i][j]=maxn;//别忘了 !!!!!!!!!!!!!!!!!!!
}//别忘了 !!!!!!!!!!!!!!!!!!!
}//别忘了 !!!!!!!!!!!!!!!!!!!
}//别忘了 !!!!!!!!!!!!!!!!!!!
for(int i=1; i<=m; ++i) {
cin>>x>>y>>z;
a[x][y]=z;
a[y][x]=z;
}
for(int i=1; i<=n; ++i) {
dis[i]=a[s][i];
}
dis[s]=0;
inq[s]=1;
for(int i=1; i<=n-1; ++i) {
int k=0;
int minn=1e9+100;
for(int j=1; j<=n; ++j) {
if((inq[j]==0)&&(dis[j]<minn)) {
minn=dis[j];
k=j;
}
}
if(k==0) break;
inq[k]=1;
for(int j=1; j<=n; ++j) {
if(dis[k]+a[k][j]<dis[j]) {
dis[j]=dis[k]+a[k][j];
}
}
}
for(int i=1; i<=n; ++i) {
cout<<dis[i]<<" ";
}
return 0;
}
/*
5 7 1
1 2 10
1 5 7
1 3 49
2 3 17
2 4 7
2 5 5
3 4 34
*/
优化
复杂度(O(n*log(n)))
利用堆(优先队列)找最近的点,避免了循环
/*
dijjstra+堆优化
*/
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<string>
#include<cstring>
#include<cmath>
#include<vector>
#include<queue>
#include<stack>
using namespace std;
const int maxn=520;
const int INF=1e9;
vector<pair<int,int> >/*edge*/e[maxn];//定义一个二维的动态数组以便以后建立邻接表
int dis[maxn],inq[maxn]/*in_queue*/;
int n,m,s,t;
void start() {
for(int i=0; i<maxn; ++i) {
e[i].clear() ;
}//如果不是多组数据可以没有
memset(inq,0,sizeof(inq));
for(int i=0; i<maxn; ++i) {
dis[i]=INF;
} //初始化dis
}
int main() {
std::ios::sync_with_stdio(false);//cin优化一下下(主要是我懒不想打scnaf)
while(cin>>n>>m) {
start();//初始化
for(int i=0; i<m; ++i) {
int x,y,z;//双向道路的起点、终点 、权值
cin>>x>>y>>z;
e[x].push_back(make_pair(y,z));//把x连到y上权值是z
e[y].push_back(make_pair(x,z));//双向的原因
}
int s,t;
cin>>s>>t;
//queue<int>q;
priority_queue< pair<int,int> >q;
//q.push(s);//将lyq家(起点入队类似于bfs)
q.push(make_pair(-dis[s],s));//pushu(-d[s])变成小根堆 ,其实也可以直接定义(不过我懒)
dis[s]=0;//从起点到起点一定距离为0
inq[s]=1;//标记一下s点入队
/*bfs阶段*/
while(!q.empty() ) {
//int now=q.front() ;//now 是现在lyq到的点
int now=q.top().second;//只需要第二个就ok
q.pop();//吃队
inq[now]=0;//更新inq
for(int i=0; i<e[now].size(); ++i) {//遍历
int v=e[now][i].first;
/*松弛操作*/
if(dis[v]>dis[now]+e[now][i].second) {
dis[v]=dis[now]+e[now][i].second;
if(inq[v]==1) continue;//如果在队列里就不管了
else {
inq[v]=1;//标记进队
//q.push(v);
q.push(make_pair(-dis[v],v));
}
}
}
}
if(dis[t]==1e9) {
cout<<"-1
";//如果最短路还是1e9那lyq就找不到了....
} else {
cout<<dis[t];
}
}
return 0;
}
spfa
就和bfs差不多,自己看代码吧
#include<bits/stdc++.h>
using namespace std;
const int maxn=99999999;
const int h=1005;
int dis[h],a[h][h],inq[h],pre[h];
int n,m,x,y,z,s;
queue<int>q;
int main() {
cin>>n>>m>>s;//别忘了 !!!!!!!!!!!!!!!!!!!
for(int i=1; i<=m; ++i) {//别忘了 !!!!!!!!!!!!!!!!!!!
for(int j=1; j<=m; ++j) {//别忘了 !!!!!!!!!!!!!!!!!!!
if(i==j) {//别忘了 !!!!!!!!!!!!!!!!!!!
a[i][j]=0;//别忘了 !!!!!!!!!!!!!!!!!!!
} else {//别忘了 !!!!!!!!!!!!!!!!!!!
a[i][j]=maxn;//别忘了 !!!!!!!!!!!!!!!!!!!
}//别忘了 !!!!!!!!!!!!!!!!!!!
}//别忘了 !!!!!!!!!!!!!!!!!!!
}//别忘了 !!!!!!!!!!!!!!!!!!!
for(int i=1; i<=m; ++i) {
dis[i]=maxn;
}
for(int i=1; i<=m; ++i) {
cin>>x>>y>>z;
a[x][y]=z;
a[y][x]=z;
}
inq[s]=1;
dis[s]=0;
q.push(s);
while(!q.empty()) {
int k=q.front() ;
q.pop();
inq[k]=0;
for(int i=1; i<=n; ++i) {
if(a[k][i]!=maxn) {
if(dis[k]+a[k][i]<dis[i]) {
dis[i]=dis[k]+a[k][i];
if(!inq[i]) {
q.push(i);
inq[i]=1;
}
}
}
}
}
for(int i=1; i<=n; ++i) {
cout<<dis[i]<<" ";
}
return 0;
}
优化
双端队列:
/*
原队列改为双端队列,对一个要加入队列的点u,如果dis[u] 小
于队首元素v的dis[v],那么就就加入到队首元素,否则加入到队尾。
*/
#include<bits/stdc++.h>
using namespace std;
const int maxn=99999999;
const int h=2505;
long long int dis[h],a[h][h],inq[h],pre[h];
int n,m,x,y,z,s;
deque<int>q;
int main() {
cin>>n>>m;//别忘了 !!!!!!!!!!!!!!!!!!!
for(int i=1; i<=m; ++i) {//别忘了 !!!!!!!!!!!!!!!!!!!
for(int j=1; j<=m; ++j) {//别忘了 !!!!!!!!!!!!!!!!!!!
if(i==j) {//别忘了 !!!!!!!!!!!!!!!!!!!
a[i][j]=0;//别忘了 !!!!!!!!!!!!!!!!!!!
} else {//别忘了 !!!!!!!!!!!!!!!!!!!
a[i][j]=maxn;//别忘了 !!!!!!!!!!!!!!!!!!!
}//别忘了 !!!!!!!!!!!!!!!!!!!
}//别忘了 !!!!!!!!!!!!!!!!!!!
}//别忘了 !!!!!!!!!!!!!!!!!!!
for(int i=1; i<=m; ++i) {
dis[i]=maxn;
}
for(int i=1; i<=m; ++i) {
cin>>x>>y>>z;
a[x][y]=z;
a[y][x]=z;
}
s=1;
inq[s]=1;
dis[s]=0;
q.push_front(s);
while(!q.empty()) {
int k=q.front() ;
q.pop_front() ;
inq[k]=0;
for(int i=1; i<=n; ++i) {
if(a[k][i]!=maxn) {
if(dis[k]+a[k][i]<dis[i]) {
dis[i]=dis[k]+a[k][i];
if(!inq[i]) {
if(dis[i]>dis[q.front()])
q.push_front(i);
else
q.push_back(i);
inq[i]=1;
}
}
}
}
}
cout<<dis[n];
return 0;
}
dfs版本
int flag=0;
int dis[N]= {};
int vis[N]= {};
void Clr() {
memset(dis,0,sizeof(dis));
memset(vis,0,sizeof(vis));
memset(first,0,sizeof(first));
cnt=1;
flag=0;
}
void SPFA(int u) {
vis[u]=1;
for(int i=first[u]; i; i=e[i].nxt) {
int v=e[i].v;
if(dis[u]+e[i].w<dis[v]) {
if(vis[v]||flag) {
flag=1;
break;
}
dis[v]x=dis[u]+e[i].w;
SPFA(v);
}
}
vis[u]=0;
}
//
for(int i=1; i<=n; i++) {
SPFA(i);
if(flag)break;
}
/*第二种*/
/*
bool spfa(int u){
vis[u] = true;
int i;
for(i = head[u]; i; i = e[i].next){
int v = e[i].to, w = e[i].w;
if(dis[v] > dis[u] + w){
dis[v] = dis[u] + w;
if(vis[v]) return false;
if(!spfa(v)) return false;
}
}
vis[u] = false;
return true;
}
*/
LLL版本:
/*
对每个要出对的元素u,比较dis[u]和队列中dis的平均值,如果dis[u]更大,
那么将它弹出放到队尾,取队首元素在进行重复判断,直至存在dis[x]小于平均值
*/
#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
const int maxn = 205;
int n, dis[maxn], sum = 0, cnt = 0;
int G[maxn][maxn] = {};
bool inq[maxn] = {};
int main() {
memset(dis, 0x3f, sizeof(dis));
cin >> n;
for (int i = 1; i < n; ++i) {
for (int j = i + 1; j <= n; ++j) {
cin >> G[i][j];
}
}
queue<int> Q;
Q.push(1);
inq[1] = true;
dis[1] = 0;
cnt = 1;
while (!Q.empty()) {
int u = Q.front();
while (dis[u]*cnt > sum) {
Q.pop();
Q.push(u);
u = Q.front();
}
Q.pop();
cnt--;
sum -= dis[u];
inq[u] = false;
for (int i = u + 1; i <= n; ++i) {
if (dis[i] > dis[u] + G[u][i]) {
dis[i] = dis[u] + G[u][i];
if (!inq[i]) {
Q.push(i);
sum += dis[i];
cnt++;
}
}
}
}
cout << dis[n];
}
几道例题
例题1

将所有的边方向取反,求从1号点到所有点的单源最短路即可。
例题2
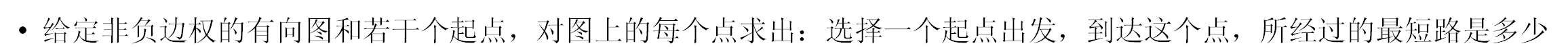
新建一个超级源点,向所有起点连一条边权为0的边,从它开始跑单源最短路。
最短路计数

在进行dijkstra算法时,额外维护一个sum数组表示到达某个点的最短路条数。在进行松弛操作时维护sum数组。
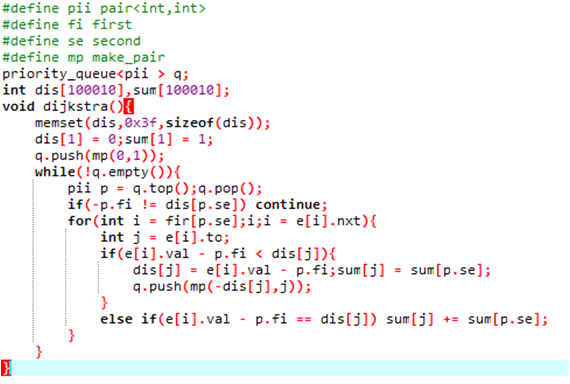
最短路输出方案

在dijkstra算法中额外记录一个数组from,表示从1号点到达它的最短路是从哪个点走过来的。
最后从n号点不断沿着from走回去即可。