朴素贝叶斯(Naïve Bayes)属于监督学习算法,实现简单,学习效率高;由于建立在贝叶斯理论之上,涉及到统计学方法,所以在大样本量下会有较好的表现,当然样本需要在一定程度上反映真实分布情况。
该算法的一条假设为:输入的特征向量的各分量之间两两条件独立。因为这条假设比较严格,能够完全符合该假设的应用场景并不多见,所以给这个算法带来了“朴素”的修饰。然儿这并不妨碍朴素贝叶斯作为一个概率分类器在文本分类方面的优异表现,特别是在垃圾邮件识别领域,朴素贝叶斯表现突出。
本文着重介绍朴素贝叶斯在分类任务上的应用(只考虑特征向量各分量均为离散值的情况,在实际应用中,遇到连续取值的变量通常也会将其离散化)。
1 问题描述
假设我们获得如下训练数据(训练集中样本数为N):
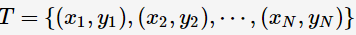
其中,x 表示特征向量(设定为n维,表示有n个离散属性值),y 表示标签变量,表征对应的特征向量代表的样本所属的类别,y 的取值范围如下(类别数为K):

预测:当特征向量为X时,标签y应取何值。
2 贝叶斯定理
贝叶斯定理是关于随机事件A和B的条件概率的一则定理:

其中 A 以及 B 为随机事件,且 P(B) 不为零。P(A|B) 是指在事件 B 发生的情况下事件 A 发生的概率。
在贝叶斯定理中,上式中的项有以下称谓:
P(A|B) 由于得自 B 的取值而被称作 A 的后验概率。
P(A) 是 A 的先验概率(或边缘概率),称为"先验"是因为不考虑 B 的情况。
3 应用贝叶斯理论解决分类问题
贝叶斯理论解决分类问题的思路如下:
输入待预测数据X,则预测类别 y 取使得 y 的后验概率最大的类别值,即:

应用贝叶斯定理:
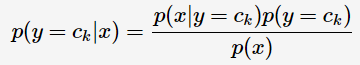
由于 y 的取值不会影响上式的分母,所以可以将上式转化为:

进一步考虑属性间的条件独立性,对于n维特征向量:

可以将它的后验概率转化为:
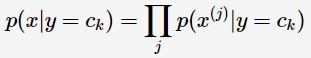
则(2)式可以转为:

选择后验概率最大的类别作为预测类别,因为已经证明:后验概率最大化可以使期望风险最小化。
到此为止,我们将类别预测问题转为后验概率的计算与比较问题;为了进一步计算,需要对(3)式中涉及的先验概率与条件概率进行估计。
4 概率估计
4.1 极大似然估计
先验概率的极大似然估计:
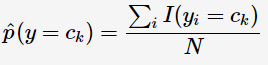
I 用于计数,用类别为Ck的样本占总样本的比例作为y取Ck值的先验概率。
特征向量的第j个属性变量的条件概率的极大似然估计:
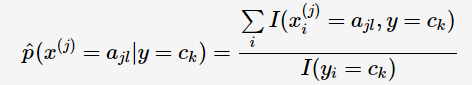
同样是将样本比例作为概率的思想。
4.2 贝叶斯估计(最大后验概率估计)
极大似然估计先验概率与条件概率时,可能出现有关样本数为0的情况,由于后验概率是多项连乘的结果,那么得到的后验概率也为0,影响分类的效果。
因此,在估计时需要做平滑处理,这种方法被称为贝叶斯估计。
先验概率的贝叶斯估计:

其中 K 为总的类别数,λ为可调参数。
特征向量的第j个属性变量的条件概率的贝叶斯估计:

其中 Sj 为第 j 个属性所取的不同的离散值的数量,λ为可调参数。
通常贝叶斯估计中的参数 λ=1 ,这时被称为Laplace平滑。