决策树:
1.决策树类似于:玩一个游戏,一个人首先在纸中写下一个事物(类型),然后,由提问者提出问题,回答问题只能使用true 或 false,提问者不断根据答案,调整问题,缩小范围,直至给出最后的答案。(假如问题个数有限)
2.决策树原理类似于这样,用户输入数据,然后输出事物类型。
3.决策树构建的过程,就是根据数据,提取一系列规则的过程(例如应该问哪些问题),也就是机器学习的过程。
准备知识:
如何使用信息论划分数据集。
问题一:当前数据集中,哪个特征值,在划分数据类型时,起到决定性作用?
*为了找到决定性的特征,必须评估每个特征(例如:在K分类中,接吻镜头和打斗镜头,决定了电影类型)。
*知道了决定性的特征后,原始数据集就会被划分为几个数据子集,这些数据子集会分布在第一个决策点的所有分支上。
*如果某个分支下的数据属于同一类型,那么就无需对数据集进行进一步划分;否则,继续重复划分数据子集。直到所有具有相同类型的数据,均在一个数据子集中。
*划分数据子集的算法,和划分原始数据集的方法相同。
//
*检测数据集中,每个子项是否属于同一分类:
if 当前节点,每个子项属于同一分类:
return
else :
寻找划分数据集的最好特征(问题一)
划分数据集(问题二)
创建分支节点
for 每个划分的子集
为子集创建分支节点
(在这里进行递归,又调用这个函数本身,判断子集是不是属于同一分类)
返回分支节点
//
问题二:如何划分数据集?(可以参考ID3算法)
*每次划分数据集时,我们只选取一个特征属性,如果训练集中,存在N个特征属性,第一次划分的时候,应该选择哪一个呢?
例如:在K邻近算法中的电影划分,应该使用动作镜头作为第一次划分的属性呢,还是接吻镜头呢。
例如:鱼类和非鱼类,在划分的时候,我们想要使用第一个特征,还是第二个特征呢?
*所以,要决定使用哪个特征,必须采取量化的方法判断。
| 不浮出水面是否可以生存 | 是否有脚蹼 | 属于鱼类 | |
| 1 | 是 | 是 | 是 |
| 2 | 是 | 是 | 是 |
| 3 | 是 | 否 | 否 |
| 4 | 否 | 是 | 否 |
| 5 | 否 | 是 | 否 |
问题一的解决方案:
*划分数据的大原则:将无序数据变得更加有序。组织杂乱无章数据的一种方法,就是使用信息论度量信息。
在划分数据集,之前,之后 的信息发生的变化,称为信息增益,知道如何计算信息增益(问题三),就可以计算每个特征值划分数据时,获得的信息增益,根据 每个特征信息增益,选取最大信息增益值的特征,从而,寻找出划分数据集的最好特征,问题一得解。
****************************************************************************************************************************************
插入知识:
1. 熵,定义为信息的期望值。
2. 如果某样事物,可以被划分在多个分类当中,那么,某个分类的信息,定义为:
l(xi) = -log2 p(xi) , 2为底数,p(xi) 为该分类的概率。( 2的l(xi)次方=p(xi))
3. 所有类别,可能包含的信息期望值(熵):
H = ∑ ( p(xi) * xi )
4.****熵越高,则混合的数据也就越多,也就是,数据中,类型越多。
**熵通常用来形容数据的混乱度,无序度。
****************************************************************************************************************************************
通过度量划分的数据集的熵,来判断当前是否正确地划分了数据集。
通过对每个特征来划分数据集,然后以其实际类型,结合熵计算公式,熵最小的那个特征,就是划分的依据。(问题一)得解。
//
//
构建决策树:
1 . 根据原始数据集,选出用来划分数据集的属性:
更具最大信息增益,获得最佳属性:
定义:最佳信息增益值 = 0
定义:最佳属性序号 = 未知
定义:基准熵 = 输入数据集的熵 // 理论上,应该是最大的熵了,因为类型最多
for 属性 in 全部属性 {
#根据属性的值,划分出N个组,(N可能为未知个数,或者指定了个数,或者根据此属性有多少个不重复的值来定,或是枚举,或是bool,或是范围)
定义:此属性的加权熵 = 0
for 组 in 全部组 {
#输入数据集中,根据此属性,提取此组的数据;
#计算权值 prob = 此类型的数据量 / 输入数据集数据量
# 计算此类型数据子集的熵(Ent)
#此属性的加权熵 + = prob * Ent
}
此属性的信息增益 = 基准熵 - 此属性的加权熵
if(此属性的信息增益 > 最佳信息增益值)
{
最佳信息增益值 = 此属性的信息增益
最佳属性序号 = 此属性序号
}
***使用二维数组比面向对象更加简洁一些。
***补充决策树过程:

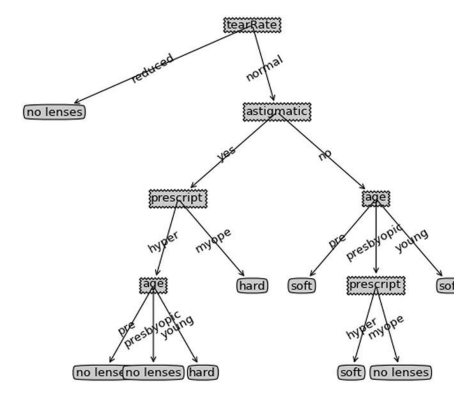
每一次在节点决策,都会去除一些已经被分类的数据,留着一些不明确类型的数据,流向下一个节点继续决策。
图一中,根据信息增益,可以挑出,第一次以No Surfacing这个属性来判断是最好的,一下子就挑出:根据某个属性的不同值,最优地分好类,而且单个子集中,数据的真实类型“纯度”最高
2. 这样的决策树,是以消耗特征来进行下一步的,(也就是说,20个问题一直问,下一个问题,永远不能和 已问过的问题 一样)。
决策树的创建过程,就是不断决定:到了某一个节点, 应该问哪些问题的过程。就是排序每个节点中,应该消耗那个特征
3. 如果在一个节点中,根据特征属性分组,如果每个组中,组内的类型都是一样的,那么就停止构建;
否则,“纯度” 最高的那个组的数据,取出类型出现最多的数据,并从原数据集中去除,然后 以下一个属性构建,直到所有特征消耗完毕。
***************************************决策树的创建过程,和使用过程,是两回事***********************************************************
存储决策树:
就是存储一个属性序列,不用像K邻近算法那样,依然从样本中寻找近邻。
存储形式: {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
*每个属性,都应该有个方法,对应返回是否继续向下判断,如果否,那么,新来的数据应该属于哪一类。